Faszination "Collatz-Problem"
Thema erstellt von Skeptika
| Beiträge: 254, Mitglied seit 10 Jahren |
Beitrag Nr. 2374-1
19.04.2022 17:09
|
Ich denke, unter Mathematik-Enthusiasten ist das Collatz-Problem wohl bekannt. Das ist übrigens ein Thema, das noch immer "offen" ist, also weder bewiesen noch wiederlegt wurde.
Für alle, die das nicht kennen, ganz kurz zur Erklärung:
Nimm eine beliebige natürliche Zahl. Ist sie durch 2 teilbar, dann teile durch zwei und rechne mit der neuen Zahl weiter.
Ist sie ungerade, dann multipliziere mit drei und addiere noch eins dazu, dann rechne mit dieser Zahl weiter.
Beispiel: 10
10 : 2 = 5
5 ist ungerade, also mal 3 (=15) und dann plus 1 (= 16)
16 : 2 = 8
8 : 2 = 4
4 : 2 = 2
2 : 2 = 1
1 = ungerade, also mal 3 plus 1 = 4
4 : 2 = 2 und hier geht es in die Schleife.
Bislang läuft es bei jeder Zahl darauf hin aus, dass man an dieses 4 - 2 - 1 Ende stößt. Mathematisch konnte man das weder beweisen noch widerlegen. Theoretisch besteht (unbewiesen!) die Möglichkeit, dass es sehr weit oben eine Schleife gibt, bei der sich die Rechenoperationen wiederholen, oder aber dass die Operationen ins Unendliche laufen...
Ich finde das Thema, das ja eigentlich so irrsinnig einfach aussieht und dennoch so kompliziert ist, wahnsinnig spannend.
Hat sich damit schonmal irgend jemand beschäftigt und vielleicht seine eigenen Gedanken dazu gemacht?978-3842349889
Für alle, die das nicht kennen, ganz kurz zur Erklärung:
Nimm eine beliebige natürliche Zahl. Ist sie durch 2 teilbar, dann teile durch zwei und rechne mit der neuen Zahl weiter.
Ist sie ungerade, dann multipliziere mit drei und addiere noch eins dazu, dann rechne mit dieser Zahl weiter.
Beispiel: 10
10 : 2 = 5
5 ist ungerade, also mal 3 (=15) und dann plus 1 (= 16)
16 : 2 = 8
8 : 2 = 4
4 : 2 = 2
2 : 2 = 1
1 = ungerade, also mal 3 plus 1 = 4
4 : 2 = 2 und hier geht es in die Schleife.
Bislang läuft es bei jeder Zahl darauf hin aus, dass man an dieses 4 - 2 - 1 Ende stößt. Mathematisch konnte man das weder beweisen noch widerlegen. Theoretisch besteht (unbewiesen!) die Möglichkeit, dass es sehr weit oben eine Schleife gibt, bei der sich die Rechenoperationen wiederholen, oder aber dass die Operationen ins Unendliche laufen...
Ich finde das Thema, das ja eigentlich so irrsinnig einfach aussieht und dennoch so kompliziert ist, wahnsinnig spannend.
Hat sich damit schonmal irgend jemand beschäftigt und vielleicht seine eigenen Gedanken dazu gemacht?
Signatur:
[Gäste dürfen nur lesen]
| Beiträge: 254, Mitglied seit 10 Jahren |
Beitrag Nr. 2374-2
21.04.2022 15:06
|
Ich frage mich, ob man beim Collatz-Problem nicht auch den umgekehrten Weg gehen könnte, indem man schaut, wie man zu den einzelnen Zahlen gelangt. Dabei gibt es einen "Hauptstrang", in welchem stets die Zahlen verdoppelt werden (was also nach Collatz umgekehrt dem "durch 2" entspricht) und dann den sich wild verzweigenden "Nebenstrang", aus dem die Zwischenzahlen entstehen...
Kann man überhaupt "unten" anfangen und dann schauen, zu welchen Zahlen man "oben" kommt? Bei den geraden Zahlen ja, aber bei den anderen?978-3842349889
Kann man überhaupt "unten" anfangen und dann schauen, zu welchen Zahlen man "oben" kommt? Bei den geraden Zahlen ja, aber bei den anderen?
Signatur:
[Gäste dürfen nur lesen]
| Beiträge: 1.734, Mitglied seit 16 Jahren |
Beitrag Nr. 2374-3
15.06.2022 05:31
|
Hallo Skeptika,
es gibt im Netz eine brillante Präsentation des Themas unter "The Simplest Math Problem No One Can Solve - Collatz Conjecture"
Die Idee von der Umkehrung macht Sinn. Nach Collatz-Hypothese wäre jede natürliche Zahl inderektes Urbild der "3x+1-Abbildung" von der 1. Mir ist bisher keine geschlossene Darstellung oder Charakterisierung der n-stufigen Urbilder bekannt und damit auch nicht der Komplementärmenge, die die Hypothese widerlegen würde.
Mein Nachweisansatz für die Collatz-Hypothese vor einger Zeit war, in einem Intervall [1,N] die längsten Ketten zu identifizeren, d.h. die Zahlen n, für die man die größte Anzahl Iteration braucht, um bei der 1 anzukommen. Wenn man so eine längste Kette immer findet, wäre die Hypothese bewiesen.
Ein Muster konnte ich identifizieren (nicht beweisen):
Mit der Zerlegung n = 6p+q ist das Bild von n modulo 6 eindeutig vom Paar (p mod 2, q) abhängig.
Längste Ketten (Länge s) sehen dann so aus:
N = 33554431: s =26, [p = 10101010101010101010101b, q = 1]
N = 67108863: s = 27, [p = 101010101010101010101010b, q = 3]
Jetzt müßte man noch zeigen, dass längste Ketten immer das alternierende Bitmuster haben, und also da sind, dann hätte man gewonnen und die Collatz-Hypothese wäre bewiesen.
Unabhängig davon kann man aus der Iteration einen Pseudo-Zufallgenerator mit guter Steruung bauen:
Die Division durch 2 in der Binärdarstellung ein Rechtsshift, z.B.
10011101001001 1 --> 10011101001001 . Wenn man das rausgeschobene Bit links wieder reingibt. 100111010010011 --> 1 1001110100100,
wird die Konvergenz gegen 1 verhindert. Die Multiplikation mit 3 leistet schliesslich das "Mischen der Bits", das eben die Vorhersage der Entwicklung beim Collatz-Problem schwer macht.
Gruß Thomas
OFFTOPIC Lese, dass Manu den Rekord-Langläufer von Claus beendet hat, Beitrag Nr. 2342-896, so bleiben uns die jüngst veröffentlichten Studien der Giftmischer :smiley3: und anhängige Mimikama-Belehrungen erspart :smiley8:
und anhängige Mimikama-Belehrungen erspart :smiley8: Ich bin begeistert!
Ich bin begeistert!
es gibt im Netz eine brillante Präsentation des Themas unter "The Simplest Math Problem No One Can Solve - Collatz Conjecture"
Die Idee von der Umkehrung macht Sinn. Nach Collatz-Hypothese wäre jede natürliche Zahl inderektes Urbild der "3x+1-Abbildung" von der 1. Mir ist bisher keine geschlossene Darstellung oder Charakterisierung der n-stufigen Urbilder bekannt und damit auch nicht der Komplementärmenge, die die Hypothese widerlegen würde.
Mein Nachweisansatz für die Collatz-Hypothese vor einger Zeit war, in einem Intervall [1,N] die längsten Ketten zu identifizeren, d.h. die Zahlen n, für die man die größte Anzahl Iteration braucht, um bei der 1 anzukommen. Wenn man so eine längste Kette immer findet, wäre die Hypothese bewiesen.
Ein Muster konnte ich identifizieren (nicht beweisen):
Mit der Zerlegung n = 6p+q ist das Bild von n modulo 6 eindeutig vom Paar (p mod 2, q) abhängig.
Längste Ketten (Länge s) sehen dann so aus:
N = 33554431: s =26, [p = 10101010101010101010101b, q = 1]
N = 67108863: s = 27, [p = 101010101010101010101010b, q = 3]
Jetzt müßte man noch zeigen, dass längste Ketten immer das alternierende Bitmuster haben, und also da sind, dann hätte man gewonnen und die Collatz-Hypothese wäre bewiesen.
Unabhängig davon kann man aus der Iteration einen Pseudo-Zufallgenerator mit guter Steruung bauen:
Die Division durch 2 in der Binärdarstellung ein Rechtsshift, z.B.
10011101001001 1 --> 10011101001001 . Wenn man das rausgeschobene Bit links wieder reingibt. 100111010010011 --> 1 1001110100100,
wird die Konvergenz gegen 1 verhindert. Die Multiplikation mit 3 leistet schliesslich das "Mischen der Bits", das eben die Vorhersage der Entwicklung beim Collatz-Problem schwer macht.
Gruß Thomas
OFFTOPIC Lese, dass Manu den Rekord-Langläufer von Claus beendet hat, Beitrag Nr. 2342-896, so bleiben uns die jüngst veröffentlichten Studien der Giftmischer :smiley3:
 und anhängige Mimikama-Belehrungen erspart :smiley8:
und anhängige Mimikama-Belehrungen erspart :smiley8:
Signatur:
Beitrag zuletzt bearbeitet von Thomas der Große am 15.06.2022 um 09:11 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 254, Mitglied seit 10 Jahren |
Beitrag Nr. 2374-4
15.06.2022 09:54
|
Thomas der Große schrieb in Beitrag Nr. 2374-3:es gibt im Netz eine brillante Präsentation des Themas unter "The Simplest Math Problem No One Can Solve - Collatz Conjecture"
Habe ich mir angesehen :smiley8:

Thomas der Große schrieb in Beitrag Nr. 2374-3:Mein Nachweisansatz für die Collatz-Hypothese vor einger Zeit war, in einem Intervall [1,N] die längsten Ketten zu identifizeren, d.h. die Zahlen n, für die man die größte Anzahl Iteration braucht, um bei der 1 anzukommen. Wenn man so eine längste Kette immer findet, wäre die Hypothese bewiesen.
Ich habe mit meinen bescheidenen Programmierkenntnissen mal ein kleines Programm geschrieben, das einfach nur der Reihe nach die Zahlen hochzählt und für jede Zahl die Zerlegungsschritte durchgeht. Ich bin beim Hochzählen bis in den Milliardenbereich vorgedrungen, aber die längste Kette hat es nicht einmal bis auf 1000 Schritte gebracht.
Thomas der Große schrieb in Beitrag Nr. 2374-3:Ein Muster konnte ich identifizieren (nicht beweisen):
Mit der Zerlegung n = 6p+q ist das Bild von n modulo 6 eindeutig vom Paar (p mod 2, q) abhängig.
Längste Ketten (Länge s) sehen dann so aus:
N = 33554431: s =26, [p = 10101010101010101010101b, q = 1]
N = 67108863: s = 27, [p = 101010101010101010101010b, q = 3]
Jetzt müßte man noch zeigen, dass längste Ketten immer das alternierende Bitmuster haben, und also da sind, dann hätte man gewonnen und die Collatz-Hypothese wäre bewiesen.
Wenn es so einfach wäre, hätten das andere vor dir sicher auch schon erkannt, oder? :smiley25:

Ein ähnlich gelagertes Problem wie das von Collatz habe ich beim Surfen gefunden. Ich stell das mal ohne Lösung ein. Wer sich daran versuchen will, dem wünsche ich viel Spaß.
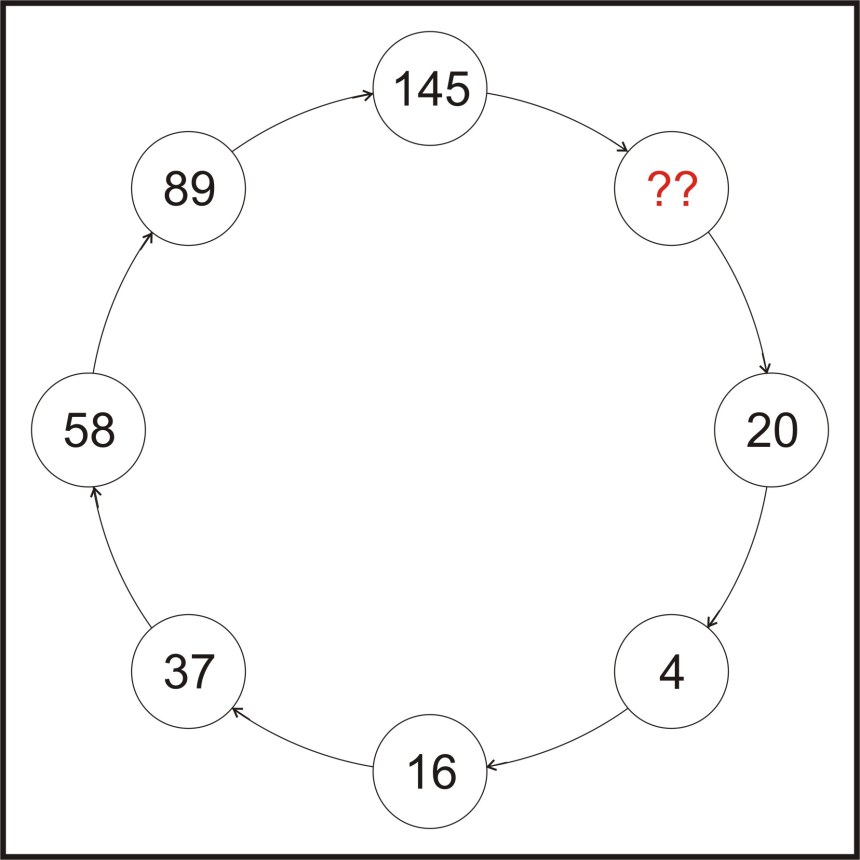
Das ist quasi das Ende der immer selben Rechenoperation (eben wie bei Collaz die Schleife 4-2-1), mit nur ganz wenigen, bekannten Ausnahmen.
Thomas der Große schrieb in Beitrag Nr. 2374-3:OFFTOPIC Lese, dass Manu den Rekord-Langläufer von Claus beendet hat, Beitrag Nr. 2342-896, so bleiben uns die jüngst veröffentlichten Studien der Giftmischer :smiley3:und anhängige Mimikama-Belehrungen erspart :smiley8:
Eben. Das Netzt füllt sich immer dramatischer mit Nachrichten zum Thema und es lässt sich schon längst nicht mehr wegdiskutieren oder als Schwurbelei abtun, dass da etwas nicht mit rechten Dingen zugeht.
Signatur:
[Gäste dürfen nur lesen]
In diesem Forum dürfen nur Mitglieder schreiben. Hier kannst du dich anmelden


 Nach oben
Nach oben