Du befindest dich hier: Manus Zeitforum
 Raum und Zeit
Raum und Zeit
 Schwarzschildradius versus 2. kosmische Geschwindigkeit
Schwarzschildradius versus 2. kosmische Geschwindigkeit
 Raum und Zeit
Raum und Zeit
 Schwarzschildradius versus 2. kosmische Geschwindigkeit
Schwarzschildradius versus 2. kosmische Geschwindigkeit
Schwarzschildradius versus 2. kosmische Geschwindigkeit
Thema erstellt von Otto
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2282-1
17.10.2017 14:17
|
Hallo, alle zusammen,
Der Schwarzschildradius berechnet sich zu
rs = 2∙G∙M /c²
Setzt man hier c = v, dann erhält man
v² = 2∙G∙M/r (1)
Diese Gleichung ist formal identisch mit der Fluchtgeschwindigkeit (zweite kosmische Geschwindigkeit), die ein (nicht rotierender) Körper mit der Masse M erreichen muß, um dessen kugelsymmetrischen Gravitationsfeld auf einer Parabelbahn zu entkommen.
Ist die Identität beider Gleichungen wirklich Zufall, wie immer zu lesen ist?
Habt Ihr andere Ideen, warum diese Gleichungen identisch sein könnten?
(1) Die aus der klassischen Physik bekannte Fluchtgeschwindigkeit basiert auf der Gleichheit von kinetischer Energie einer Masse m mit der Bindungsenergie des Gravitationsfeldes infolge der Masse M und beschreibt den Punkt des Verlassens des Gravitationsfeldes 0,5∙m∙v² = G∙M∙m/r .
Für die Beantwortung dieser Frage siehe Beitrag Nr. 2282-20 weiter unten.
Der Schwarzschildradius berechnet sich zu
rs = 2∙G∙M /c²
Setzt man hier c = v, dann erhält man
v² = 2∙G∙M/r (1)
Diese Gleichung ist formal identisch mit der Fluchtgeschwindigkeit (zweite kosmische Geschwindigkeit), die ein (nicht rotierender) Körper mit der Masse M erreichen muß, um dessen kugelsymmetrischen Gravitationsfeld auf einer Parabelbahn zu entkommen.
Ist die Identität beider Gleichungen wirklich Zufall, wie immer zu lesen ist?
Habt Ihr andere Ideen, warum diese Gleichungen identisch sein könnten?
(1) Die aus der klassischen Physik bekannte Fluchtgeschwindigkeit basiert auf der Gleichheit von kinetischer Energie einer Masse m mit der Bindungsenergie des Gravitationsfeldes infolge der Masse M und beschreibt den Punkt des Verlassens des Gravitationsfeldes 0,5∙m∙v² = G∙M∙m/r .
Für die Beantwortung dieser Frage siehe Beitrag Nr. 2282-20 weiter unten.
Beitrag zuletzt bearbeitet von Otto am 04.11.2017 um 06:08 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 1.644, Mitglied seit 16 Jahren |
Beitrag Nr. 2282-2
18.10.2017 09:35
|
Hallo Otto,
ich habe über Deine Frage nachgedacht und versuche mal eine Antwort zu finden.
Zu diesem Zweck betrachte ich den Elektromagnetismus in seiner quantisierten Form als Photonen. Ein Photon ist ein Energieträger und hat als solcher Masse.
Der Schwarzschildradius ist die Grenze, an der die Schwerkraftwirkung (bzw. die Krümmung der Raumzeit) so stark wird, dass ein Photon in Richtung der Masse, die die Schwerkraftwirkung erzeugt, gezogen wird.
Wenn nun in der zweiten von Dir genannten Formel betreffend die Fluchtgeschwindigkeit angenommen wird, dass v = c ist, betrachtest Du nur noch Photonen; denn andere massebehaftete Objekte können die Lichtgeschwindigkeit nicht erreichen.
Mit anderen Worten: In beiden Fällen (Formeln) sind Photonen Gegenstand der Betrachtung. Möglicherweise resultiert die Gleichheit der Formeln aus diesem Zusammenhang.
MfG
HartiWichtig ist, dass man nicht aufhört zu fragen. A.E.
ich habe über Deine Frage nachgedacht und versuche mal eine Antwort zu finden.
Zu diesem Zweck betrachte ich den Elektromagnetismus in seiner quantisierten Form als Photonen. Ein Photon ist ein Energieträger und hat als solcher Masse.
Der Schwarzschildradius ist die Grenze, an der die Schwerkraftwirkung (bzw. die Krümmung der Raumzeit) so stark wird, dass ein Photon in Richtung der Masse, die die Schwerkraftwirkung erzeugt, gezogen wird.
Wenn nun in der zweiten von Dir genannten Formel betreffend die Fluchtgeschwindigkeit angenommen wird, dass v = c ist, betrachtest Du nur noch Photonen; denn andere massebehaftete Objekte können die Lichtgeschwindigkeit nicht erreichen.
Mit anderen Worten: In beiden Fällen (Formeln) sind Photonen Gegenstand der Betrachtung. Möglicherweise resultiert die Gleichheit der Formeln aus diesem Zusammenhang.
MfG
Harti
Signatur:
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2282-3
18.10.2017 14:29
|
Harti schrieb in Beitrag Nr. 2282-2:Wenn nun in der zweiten von Dir genannten Formel betreffend die Fluchtgeschwindigkeit angenommen wird, dass v = c ist, betrachtest Du nur noch Photonen; denn andere massebehaftete Objekte können die Lichtgeschwindigkeit nicht erreichen. i
Hallo Harti,
mir waren nur drei wesentliche Merkmale zwischen den Gleichungen eingefallen, die Unterschiede zeigen, aber keine Begründung zur Identität der Gleichungen darstellen.
- Die Fluchtgeschwindigkeit bezieht sich auf das Verlassen von der Masse M, während der Schwarzschildradius sich auf eine Bewegung hin zu der Masse M bezieht.
- Die Fluchtgeschwindigkeit bezieht sich auf Teilchen mit Masse, während der Schwarzschildradius sich auf die Ablenkung von masselosen Teilchen (Photonen) bezieht.
- Mit Erreichen der zweiten kosmischen Geschwindigkeit verlässt eine Masse m eine stabile elliptische Bahn um die Masse M , während nach der Schwarzschild-Metrik der kreisförmige Ereignishorizont - geometrisch als Kugelkalotte beschreibbar - erreicht wird.
Photonen haben nur eine relativistische Masse, abgeleitet aus der Energie E = h∙f.
Nur diese relativistische Masse m = h∙f/c² bewirkt, daß Photonen von Gravitationsfeldern abgelenkt werden.
Aber, wie gesagt, aus diesen Einzelheiten kann ich noch keinen Grund zur Identität beider Gleichungen erkennen.
An einen Zufall kann ich hier einfach nicht so recht glauben.
Signatur:
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2282-4
18.10.2017 14:53
|
Otto schrieb in Beitrag Nr. 2282-1:Der Schwarzschildradius berechnet sich zu ...
Hier noch einige Ergänzungen zum besseren Verständnis des Schwarzschildradius
rs = 2∙M' = 2∙G∙M /c²
M ist die gravitierenden Zentralmasse
Mꞌ ist die Wirkdistanz , der s.g. Gravitationsradius
Folgende Graphik veranschaulicht, wie die aus dem Unendlichen kommenden parallelen Lichtteilchen in Richtung einer Masse M abgelenkt werden.
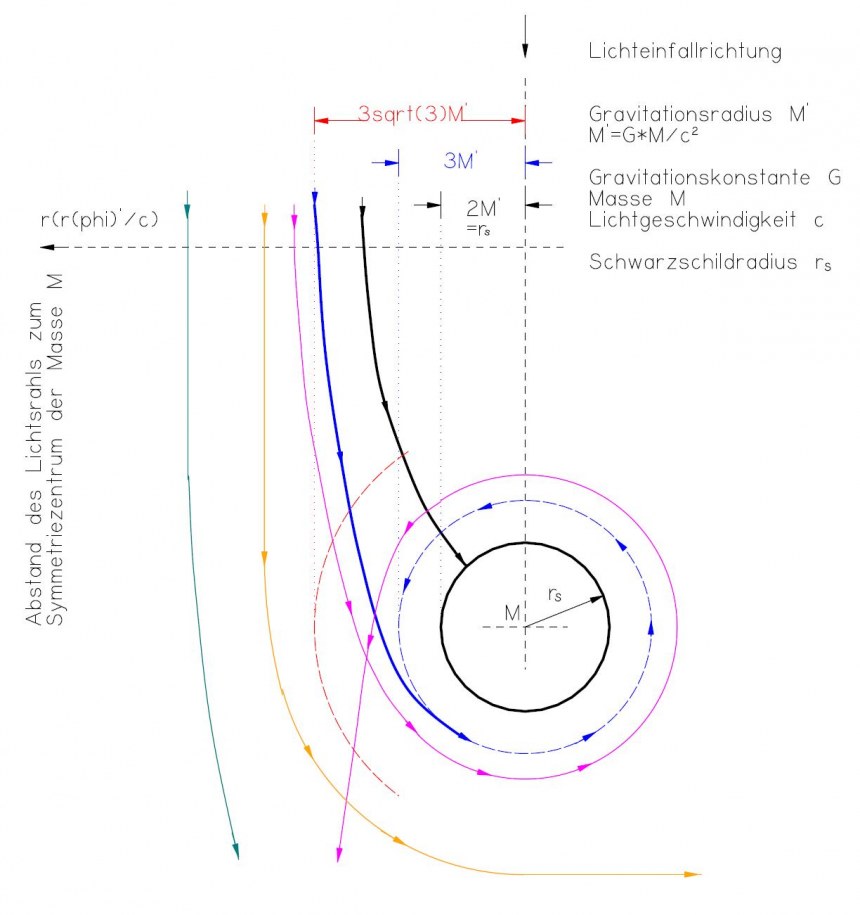
- Solange der Abstand des Lichtstrahls < 3√3 M' ist, dringt der Strahl bis zur Grenze r = 2Mꞌ = rs vor und endet dort (schwarze Kurve). Die Geschwindigkeit des Photons wird mit Erreichen des Schwarzschild-Radius rs zu Null und die Zeit logarithmisch unendlich (bezogen auf die Systemzeit t eines hinreichend weit entfernten unbewegten Beobachters). Die Zeit wird für diesen Beobachter nicht Null, sondern die Zustandsänderungen verlaufen nur extrem langsam bei Annäherung an rs.
- Für den Abstand = 3∙√3∙M' endet der Lichtstrahl im Kreis mit r=3Mꞌ=1,5rs und somit in einen labilen Zustand (blaue Kurve).
- Für den Abstand > 3∙√3∙M' setzt sich der Strahl schwächer abgelenkt ins Unendliche fort (pinkfarbene, beigefarbene und dunkelgrüne Kurven).
Anmerkungen:
- φ (phi) ist der Winkel des Lichtstrahls gegen das Symmetriezentrum.
- φ' ist die Änderung des Winkels nach der Eigenzeit τ, nicht nach der Systemzeit t.
Signatur:
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 2282-5
30.10.2017 02:23
|
Hallo Otto,
Setzt man [2] in [1] ein, so ergibt sich:
uy2 = 2 G M/r
d.h. der zur Verlangsamung des Lichts (in transversaler Richtung) im Gravitationsfeld "abgezweigte" Anteil seiner Geschwindigkeit entspräche der jeweiligen Fluchtgeschwindigkeit im Abstand r vom Gravitationszentrum.
Claus schrieb in Beitrag Nr. 2239-89:uy2/c2 = rs/r [1]
... dem Aufenthalt an einem konstanten Gravitationspotenzial könnte man eine ebenfalls konstante Geschwindigkeitskomponente in Richtung Gravitationszentrum zuordnen.
Otto schrieb in Beitrag Nr. 2282-1:Der Schwarzschildradius berechnet sich zu
rs = 2∙G∙M /c² [2]
Setzt man hier c = v, dann erhält man
v² = G∙M∙m /r (1)
Diese Gleichung ist formal identisch mit der Fluchtgeschwindigkeit (zweite kosmische Geschwindigkeit), die ein (nicht rotierender) Körper mit der Masse M erreichen muß, um dessen kugelsymmetrischen Gravitationsfeld auf einer Parabelbahn zu entkommen.
Ist die Identität beider Gleichungen wirklich Zufall, wie immer zu lesen ist?
Habt Ihr andere Ideen, warum diese Gleichungen identisch sein könnten?
Setzt man [2] in [1] ein, so ergibt sich:
uy2 = 2 G M/r
d.h. der zur Verlangsamung des Lichts (in transversaler Richtung) im Gravitationsfeld "abgezweigte" Anteil seiner Geschwindigkeit entspräche der jeweiligen Fluchtgeschwindigkeit im Abstand r vom Gravitationszentrum.
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2282-6
31.10.2017 04:52
|
Hallo Claus,
ich hätte meinen Beitrag Nr. 2239-92 besser hier anordnen sollen, um die Diskussion über Neutrinos und Gravitationswellen nicht zu stören.
Deshalb hier an dieser Stellen noch eine Ergänzung:
Der Betrag der Geschwindigkeit u des abgelenkten Lichtes wäre an einer Stelle r
│u│² = c² (x² + x4)
Dieser Betrag wäre in eine x-Komponente oder y-Komponente zu zerlegen.
Wie schon erwähnt, hat das Gravitationsfeld die Wirkung wie ein optisches Medium mit einem Brechungsindex (der von Ort r zu Ort r verschieden ist).
Die Winkelablenkung ist allerdings ca. doppelt so groß wie in der Optik, verursacht durch zwei Wirkungen, der Verkürzung der Bewegungsbahn (SRT) und der gravitativen Wirkung (SRT).
Die Gleichung für die zweite kosmische Geschwindigkeit v²=2GM'/r berücksichtigt nur die Massenträgheit und ist etwas ungenau.
Diese aus der klassischen Physik bekannte Gleichung ist nicht ganz exakt. Unter Berücksichtigung der ART berechnet sich die radiale Fluchtgeschwindigkeit genauer nach
v²=(2GM'/r)/(1-rs⁄r)
oder auch geschrieben v²=(2GM'/r)/x
Diese Gleichung ist mit der nach Newton bis auf dem Faktor 1/x identisch.
Erst mit steigendem Abstand r vom Schwerpunkt konvergiert das Verhältnis von Flucht- und Kreisbahngeschwindigkeit mit dem Wert im Nenner von (1 - rs/r) → 1. Nur für r gegen Unendlich ist die Fluchtgeschwindigkeit identisch mit der Gleichung v²=2GM'/r aus der klassischen Physik.
Die Kreisbahngeschwindigkeit v wäre also etwas höher als die nach der von Newton ermittelten zweiten kosmischen Geschwindigkeit.
Zudem bedeutet diese exaktere Gleichung zusätzlich eine Richtungsabhängigkeit resultierend aus dem tieferen Verständnis des Schwarzschildradius.
Das hat seinen Grund darin, dass im Gravitationsfeld der Raum nicht euklidisch ist. Hier ist der Umfang eines Kreises kleiner als 2πur mit πu ≈ 3,14.
Das Ganze führt aber immer noch nicht zu einer Erklärung der formalen Identität der Gleichungen für die zweite kosmische Geschwindigkeit und der Gleichung des Schwarzschildradius.
Ich vermute eher eine Lösung in Analogie zum Lagrange-Punkt L1.Traue nie Deinen Sinnen.
ich hätte meinen Beitrag Nr. 2239-92 besser hier anordnen sollen, um die Diskussion über Neutrinos und Gravitationswellen nicht zu stören.
undOtto schrieb in Beitrag Nr. 2239-92:ich bin im Zweifel, ob man so einfach ut = ux setzen kann.
Sowohl Richtung als auch Betrag von ut ändern sich in (einem polaren und auch in einem kartesischen Koordinatensystem) in Abhängigkeit von r ständig.
Auch für einen festen Punkt auf der Bahn des Lichtstrahl würde sich ux aus der Summe einer Komponente von ut einer Komponente von ur zusammensetzen.
Otto schrieb in Beitrag Nr. 2239-88:Die von Shapiro verwendeten Polarkoordinaten zeigen folgende Zusammenhänge der Geschwindigkeitskomponenten eines Photons mit der Geschwindigkeit c (für einen hinreichend weit entfernten Beobachter):
Transversale Bewegungskomponente ut = c·x
Radiale Bewegungskomponente ur = c·x²
mit x = sqrt(1-rs/r) und rs = 2M' = Schwarzschildradius.
Es gibt also einen richtungsabhängigen Zusammenhang der Geschwindigkeitskomponenten, aber die Komponenten lassen sich nicht vektoriell (wie in einem Kreis nach dem Satz des Pythagoras) zusammensetzen.
Deshalb hier an dieser Stellen noch eine Ergänzung:
Der Betrag der Geschwindigkeit u des abgelenkten Lichtes wäre an einer Stelle r
│u│² = c² (x² + x4)
Dieser Betrag wäre in eine x-Komponente oder y-Komponente zu zerlegen.
Wie schon erwähnt, hat das Gravitationsfeld die Wirkung wie ein optisches Medium mit einem Brechungsindex (der von Ort r zu Ort r verschieden ist).
Die Winkelablenkung ist allerdings ca. doppelt so groß wie in der Optik, verursacht durch zwei Wirkungen, der Verkürzung der Bewegungsbahn (SRT) und der gravitativen Wirkung (SRT).
Ich vermute, daß uns dieser Gedankenweg nicht weiterführt.Claus schrieb in Beitrag Nr. 2282-5:Setzt man [2] in [1] ein, so ergibt sich:
uy2 = 2 G M/r
d.h. der zur Verlangsamung des Lichts (in transversaler Richtung) im Gravitationsfeld "abgezweigte" Anteil seiner Geschwindigkeit entspräche der jeweiligen Fluchtgeschwindigkeit im Abstand r vom Gravitationszentrum.
Die Gleichung für die zweite kosmische Geschwindigkeit v²=2GM'/r berücksichtigt nur die Massenträgheit und ist etwas ungenau.
Diese aus der klassischen Physik bekannte Gleichung ist nicht ganz exakt. Unter Berücksichtigung der ART berechnet sich die radiale Fluchtgeschwindigkeit genauer nach
v²=(2GM'/r)/(1-rs⁄r)
oder auch geschrieben v²=(2GM'/r)/x
Diese Gleichung ist mit der nach Newton bis auf dem Faktor 1/x identisch.
Erst mit steigendem Abstand r vom Schwerpunkt konvergiert das Verhältnis von Flucht- und Kreisbahngeschwindigkeit mit dem Wert im Nenner von (1 - rs/r) → 1. Nur für r gegen Unendlich ist die Fluchtgeschwindigkeit identisch mit der Gleichung v²=2GM'/r aus der klassischen Physik.
Die Kreisbahngeschwindigkeit v wäre also etwas höher als die nach der von Newton ermittelten zweiten kosmischen Geschwindigkeit.
Zudem bedeutet diese exaktere Gleichung zusätzlich eine Richtungsabhängigkeit resultierend aus dem tieferen Verständnis des Schwarzschildradius.
Das hat seinen Grund darin, dass im Gravitationsfeld der Raum nicht euklidisch ist. Hier ist der Umfang eines Kreises kleiner als 2πur mit πu ≈ 3,14.
Das Ganze führt aber immer noch nicht zu einer Erklärung der formalen Identität der Gleichungen für die zweite kosmische Geschwindigkeit und der Gleichung des Schwarzschildradius.
Ich vermute eher eine Lösung in Analogie zum Lagrange-Punkt L1.
Signatur:
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 2282-7
31.10.2017 10:11
|
Hallo Otto,
ist das nicht "doppelt gemoppelt"?
Die Faktoren sqrt(1-v2/c2) bzw. sqrt(1-rs/r) stellen die jeweiligen Lorentzfaktoren dar.
Die in meinem Beitrag Nr. 2239-89 abgeleitete Entsprechung
berücksichtigt diese also m.E. bereits. Setzt man bspw. in die Gleichung
für r den Schwarzschildradius rs ein so erhält man mit
uy2 = c2
d.h. am Schwarzschildradius wird die Fluchtgeschwindigkeit "c" erreicht.
Gemäß der von dir vorgeschlagenen Gleichung:
würde die Fluchtgeschwindigkeit dagegen am Schwarzschildradius unendlich werden, was m.E. so nicht korrekt wäre, oder?
ist das nicht "doppelt gemoppelt"?
Die Faktoren sqrt(1-v2/c2) bzw. sqrt(1-rs/r) stellen die jeweiligen Lorentzfaktoren dar.
Die in meinem Beitrag Nr. 2239-89 abgeleitete Entsprechung
Claus schrieb in Beitrag Nr. 2239-89:uy2/c2 = rs/r
berücksichtigt diese also m.E. bereits. Setzt man bspw. in die Gleichung
Claus schrieb in Beitrag Nr. 2282-5:uy2 = 2 G M/r
für r den Schwarzschildradius rs ein so erhält man mit
Otto schrieb in Beitrag Nr. 2282-1:Der Schwarzschildradius berechnet sich zu rs = 2∙G∙M /c²
uy2 = c2
d.h. am Schwarzschildradius wird die Fluchtgeschwindigkeit "c" erreicht.
Gemäß der von dir vorgeschlagenen Gleichung:
Otto schrieb in Beitrag Nr. 2282-6:Unter Berücksichtigung der ART berechnet sich die radiale Fluchtgeschwindigkeit genauer nach
v²=(2GM'/r)/(1-rs⁄r)
würde die Fluchtgeschwindigkeit dagegen am Schwarzschildradius unendlich werden, was m.E. so nicht korrekt wäre, oder?
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2282-8
31.10.2017 17:06
|
Hallo Claus,
Der dimensionslose Lorenzfaktor 1/sqrt(1-v2/c2), der die Zeit-/Längenkontraktion beschreibt, ist klar. Er gilt nur für die SRT, ohne Berücksichtigung von gravitativen Massen.
Warum sollte sqrt(1-rs/r) in Analogie auch ein Lorenzfaktor sein?
Ist c die größte erreichbare Geschwindigkeit, dann kann nur die Resultierende aus ur und ut diesen Wert annehmen.
Dann ist u² = c² = c²(x²+x4)
Nach Einsetzen von x=sqrt(1-rs/r) und Umstellung erhalte ich nur die Gleichung
1 + 3(rs/r) + (rs/r)² = 0
Die Gleichung habe ich von Wikipedia/Fluchtgeschwindigkeit. (1)
Der Abschnitt "Fluchtgeschwindigkeit von einem schwarzen Loch" beschreibt den Zusammenhang zwischen Fluchtgeschwindigkeit unter der Wirkung der Masse eines SL.
Zitat: "Während die Fluchtgeschwindigkeit erst am Ereignishorizont des schwarzen Loches, bei r=rs, die Lichtgeschwindigkeit c erreicht, ist die Kreisbahngeschwindigkeit schon bei r=1,5rs (an der sogenannten Photonensphäre) gleich c und bis 2rs größer als die radiale Fluchtgeschwindigkeit."
Gruß, Otto
(1) Die Gleichung hatte ich auch noch woanders im Internet gefunden, kann die Stelle aber im Moment nicht wiederfinden.Traue nie Deinen Sinnen.
Das kann ich noch nicht nachvollziehen.Claus schrieb in Beitrag Nr. 2282-7:Die Faktoren sqrt(1-v2/c2) bzw. sqrt(1-rs/r) stellen die jeweiligen Lorentzfaktoren dar.
Der dimensionslose Lorenzfaktor 1/sqrt(1-v2/c2), der die Zeit-/Längenkontraktion beschreibt, ist klar. Er gilt nur für die SRT, ohne Berücksichtigung von gravitativen Massen.
Warum sollte sqrt(1-rs/r) in Analogie auch ein Lorenzfaktor sein?
Diesen Gedankengang kann ich immer noch nicht nachvollziehen.Claus schrieb in Beitrag Nr. 2282-7:uy2 = c2
d.h. am Schwarzschildradius wird die Fluchtgeschwindigkeit "c" erreicht.
Ist c die größte erreichbare Geschwindigkeit, dann kann nur die Resultierende aus ur und ut diesen Wert annehmen.
Dann ist u² = c² = c²(x²+x4)
Nach Einsetzen von x=sqrt(1-rs/r) und Umstellung erhalte ich nur die Gleichung
1 + 3(rs/r) + (rs/r)² = 0
Claus schrieb in Beitrag Nr. 2282-7:Gemäß der von dir vorgeschlagenen Gleichung:
Otto schrieb in Beitrag Nr. 2282-6:
Unter Berücksichtigung der ART berechnet sich die radiale Fluchtgeschwindigkeit genauer nach
v²=(2GM'/r)/(1-rs⁄r)
würde die Fluchtgeschwindigkeit dagegen am Schwarzschildradius unendlich werden, was m.E. so nicht korrekt wäre, oder?
Die Gleichung habe ich von Wikipedia/Fluchtgeschwindigkeit. (1)
Der Abschnitt "Fluchtgeschwindigkeit von einem schwarzen Loch" beschreibt den Zusammenhang zwischen Fluchtgeschwindigkeit unter der Wirkung der Masse eines SL.
Zitat: "Während die Fluchtgeschwindigkeit erst am Ereignishorizont des schwarzen Loches, bei r=rs, die Lichtgeschwindigkeit c erreicht, ist die Kreisbahngeschwindigkeit schon bei r=1,5rs (an der sogenannten Photonensphäre) gleich c und bis 2rs größer als die radiale Fluchtgeschwindigkeit."
Gruß, Otto
(1) Die Gleichung hatte ich auch noch woanders im Internet gefunden, kann die Stelle aber im Moment nicht wiederfinden.
Signatur:
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 2282-9
31.10.2017 19:18
|
Hallo Otto,
Der in deiner Gleichung verwendete Faktor bezieht sich aber auf die (aus dem Off) beobachtete Kreisbahngeschwindigkeit, nicht auf die Fluchtgeschwindigkeit:
Die (radiale) Fluchtgeschwindigkeit erreicht dagegen erst am Ereignishorizont die Lichtgeschwindigkeit:
Daher darfst du den Faktor m.E. nicht für die Fluchtgeschwindigkeit einsetzen, denn bei r = rs wäre die Fluchtgeschwindigkeit sonst nicht c, sondern unendlich.
Otto schrieb in Beitrag Nr. 2282-8:Die Gleichung habe ich von Wikipedia/Fluchtgeschwindigkeit. (1)
Der Abschnitt "Fluchtgeschwindigkeit von einem schwarzen Loch" beschreibt den Zusammenhang zwischen Fluchtgeschwindigkeit unter der Wirkung der Masse eines SL.
Zitat: "Während die Fluchtgeschwindigkeit erst am Ereignishorizont des schwarzen Loches, bei r=rs, die Lichtgeschwindigkeit c erreicht, ist die Kreisbahngeschwindigkeit schon bei r=1,5rs (an der sogenannten Photonensphäre) gleich c und bis 2rs größer als die radiale Fluchtgeschwindigkeit."
Der in deiner Gleichung verwendete Faktor bezieht sich aber auf die (aus dem Off) beobachtete Kreisbahngeschwindigkeit, nicht auf die Fluchtgeschwindigkeit:
Zitat von Wikipedia:... ist die Kreisbahngeschwindigkeit höher als nach Newton, um den Faktor 1 / sqrt(1 − rs/r)
Die (radiale) Fluchtgeschwindigkeit erreicht dagegen erst am Ereignishorizont die Lichtgeschwindigkeit:
Zitat von Wikipedia:... berechnet sich die radiale Fluchtgeschwindigkeit wie nach Newton, ... Während die Fluchtgeschwindigkeit erst am Ereignishorizont des schwarzen Loches, bei r = rs die Lichtgeschwindigkeit c erreicht, ist die Kreisbahngeschwindigkeit schon bei r = 1,5 rs gleich c. ...
Daher darfst du den Faktor m.E. nicht für die Fluchtgeschwindigkeit einsetzen, denn bei r = rs wäre die Fluchtgeschwindigkeit sonst nicht c, sondern unendlich.
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 2282-10
31.10.2017 20:48
|
Otto schrieb in Beitrag Nr. 2282-8:Warum sollte sqrt(1-rs/r) in Analogie auch ein Lorenzfaktor sein?
Weil er die Newtonsche Theorie für den relativistischen Fall korrigiert, dass r gegen rs geht.
Claus schrieb in Beitrag Nr. 2282-7:uy2 = c2
d.h. am Schwarzschildradius wird die Fluchtgeschwindigkeit "c" erreicht.
Zitat von Otto:Diesen Gedankengang kann ich immer noch nicht nachvollziehen.
Ich meine mit uy die sogenannte radiale Fluchtgeschwindigkeit, nicht den radialen Anteil der Kreisbahngeschwindigkeit.
Die radiale Fluchtgeschwindigkeit erreicht am Schwarzschildradius den Wert c.
Der Betrag von uy (das enspräche der Projektion des roten Vektors meiner Grafik in Beitrag-Nr. 2239-85 auf die grüne y-Achse) entspricht entsprechend der Ableitung der Formel m.E. immer dieser so definierten "radialen Fluchtgeschwindigkeit".
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2282-11
01.11.2017 21:24
|
Hallo Claus,
ich werde versuchen, die vielen angesprochenen Themen Stück für Stück in separaten Beiträgen zu bearbeiten, um die Übersichtlichkeit zu wahren.
Zum ersten Thema "relativistische Fluchtgeschwindigkeit":
Du hast recht, man muß sehr genau zwischen radialer Fluchtgeschwindigkeit und transversaler Kreisbahngeschwindigkeit unterscheiden.
Umgangssprachlich wird jedoch die (erste und zweite kosmische Geschwindigkeit) als Fluchtgeschwindigkeit bezeichnet, obwohl eine tangentiale Kreisbahngeschwindigkeit gemeint ist, was natürlich zu Verwirrungen führen muß.
Ich versuche mal eine Zusammenfassung, auch Dank Deiner Gedanken via PN.
Die tangentiale Kreisbahngeschwindigkeit (erste kosmische Geschwindigkeit) einer Testmasse um eine Zentralmasse M auf einer konzentrischen Kreisbahn im niedrigsten Orbit „r = r1“ ist relativistisch
vt1² = (GM/r)/(1-rs/r)
Die tangentiale Geschwindigkeit auf einer geschlossenen Bahn (zweite kosmische Geschwindigkeit) einer Testmasse um eine Zentralmasse M mit „r = r2“ wäre
vt2² <= (2GM/r)/(1-rs/r)
Ist die Umlaufgeschwindigkeit v > vt2, dann schwenkt die Testmasse auf eine offene Parabelbahn.
Das Verhältnis von zweiter zu erster kosmischer Geschwindigkeit ist
(vt1/vt2)² = 2
Zur Berechnung des Radius r2 wird folgende Gleichung für den Schwarzschildradius verwendet:
rs = 2Mꞌ = 2GM/c²
Für den Fall r2 = 1.5∙rs (rs/r2 = 2/3) resultiert daraus
vt2² = (2GM/r2)/(1-rs/r2) = (2GM/(1,5∙rs)) 3) = 2GM/rs = c²∙(2GM/2GM) =c²
vt2 = c
Die Kreisbahngeschwindigkeit vt2 (zweite kosmische Geschwindigkeit) erreicht also bereits die Lichtgeschwindigkeit c bei einem Radius von 1,5∙rs , während Fluchtgeschwindigkeit c erst am Ereignishorizont rs des Schwarzen Loches erreicht wird.
Meine ursprüngliche Frage zu Thema "Schwarzschildradius versus 2. kosmische Geschwindigkeit" war
Mein Fazit heute:
Die Formeln kann man so nicht gleich setzen, weil die Gleichung für die Fluchtgeschwindigkeit den relativistischen Anteil nicht berücksichtigt (Faktor 1/(1-rs⁄r) .Traue nie Deinen Sinnen.
ich werde versuchen, die vielen angesprochenen Themen Stück für Stück in separaten Beiträgen zu bearbeiten, um die Übersichtlichkeit zu wahren.
Zum ersten Thema "relativistische Fluchtgeschwindigkeit":
Claus schrieb in Beitrag Nr. 2282-9:Hallo Otto,
Otto schrieb in Beitrag Nr. 2282-8:
Die Gleichung habe ich von Wikipedia/Fluchtgeschwindigkeit.
Der Abschnitt "Fluchtgeschwindigkeit von einem schwarzen Loch" beschreibt den Zusammenhang zwischen Fluchtgeschwindigkeit unter der Wirkung der Masse eines SL.
Zitat: "Während die Fluchtgeschwindigkeit erst am Ereignishorizont des schwarzen Loches, bei r=rs, die Lichtgeschwindigkeit c erreicht, ist die Kreisbahngeschwindigkeit schon bei r=1,5rs (an der sogenannten Photonensphäre) gleich c und bis 2rs größer als die radiale Fluchtgeschwindigkeit."
Claus:
Der in deiner Gleichung verwendete Faktor bezieht sich aber auf die (aus dem Off) beobachtete Kreisbahngeschwindigkeit, nicht auf die Fluchtgeschwindigkeit:
Zitat von Wikipedia:
... ist die Kreisbahngeschwindigkeit höher als nach Newton, um den Faktor 1 / sqrt(1 − rs/r)
Die (radiale) Fluchtgeschwindigkeit erreicht dagegen erst am Ereignishorizont die Lichtgeschwindigkeit: ...
Du hast recht, man muß sehr genau zwischen radialer Fluchtgeschwindigkeit und transversaler Kreisbahngeschwindigkeit unterscheiden.
Umgangssprachlich wird jedoch die (erste und zweite kosmische Geschwindigkeit) als Fluchtgeschwindigkeit bezeichnet, obwohl eine tangentiale Kreisbahngeschwindigkeit gemeint ist, was natürlich zu Verwirrungen führen muß.
Ich versuche mal eine Zusammenfassung, auch Dank Deiner Gedanken via PN.
Die tangentiale Kreisbahngeschwindigkeit (erste kosmische Geschwindigkeit) einer Testmasse um eine Zentralmasse M auf einer konzentrischen Kreisbahn im niedrigsten Orbit „r = r1“ ist relativistisch
Die tangentiale Geschwindigkeit auf einer geschlossenen Bahn (zweite kosmische Geschwindigkeit) einer Testmasse um eine Zentralmasse M mit „r = r2“ wäre
Ist die Umlaufgeschwindigkeit v > vt2, dann schwenkt die Testmasse auf eine offene Parabelbahn.
Das Verhältnis von zweiter zu erster kosmischer Geschwindigkeit ist
Zur Berechnung des Radius r2 wird folgende Gleichung für den Schwarzschildradius verwendet:
Für den Fall r2 = 1.5∙rs (rs/r2 = 2/3) resultiert daraus
vt2² = (2GM/r2)/(1-rs/r2) = (2GM/(1,5∙rs)) 3) = 2GM/rs = c²∙(2GM/2GM) =c²
Die Kreisbahngeschwindigkeit vt2 (zweite kosmische Geschwindigkeit) erreicht also bereits die Lichtgeschwindigkeit c bei einem Radius von 1,5∙rs , während Fluchtgeschwindigkeit c erst am Ereignishorizont rs des Schwarzen Loches erreicht wird.
Meine ursprüngliche Frage zu Thema "Schwarzschildradius versus 2. kosmische Geschwindigkeit" war
Otto schrieb in Beitrag Nr. 2282-1:Der Schwarzschildradius berechnet sich zu
rs = 2∙G∙M /c²
Setzt man hier c = v, dann erhält man
v² = 2∙G∙M /rv² = G∙M∙m /r
Diese Gleichung ist formal identisch mit der Fluchtgeschwindigkeit (zweite kosmische Geschwindigkeit), die ein (nicht rotierender) Körper mit der Masse M erreichen muß, um dessen kugelsymmetrischen Gravitationsfeld auf einer Parabelbahn zu entkommen.
Ist die Identität beider Gleichungen wirklich Zufall, wie immer zu lesen ist?
Mein Fazit heute:
Die Formeln kann man so nicht gleich setzen, weil die Gleichung für die Fluchtgeschwindigkeit den relativistischen Anteil nicht berücksichtigt (Faktor 1/(1-rs⁄r) .
Signatur:
Beitrag zuletzt bearbeitet von Otto am 02.11.2017 um 22:21 Uhr.
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 2282-12
02.11.2017 03:57
|
Hallo Otto,
In der Gleichung für die Fluchtgeschwindigkeit muss man den Faktor 1/(1-rs⁄r) m.E. nicht berücksichtigen, weil hier nicht der Abstand vom Gravitationszentrum r sondern die bewegte Probemasse m relativistisch zu behandeln wäre. Die Fluchtgeschwindigkeit ist aber von der Probemasse unabhängig, weil sie auf beiden Seiten der Gleichung
auftaucht, sich deren Einfluss also herauskürzt.
In der resultierenden Gleichung v2 = 2 GM/r "setzt" man dann rs definitionsgemäß als denjenigen Abstand, bei dem die Fluchtgeschwindigkeit die Lichtgeschwindigkeit erreicht.
Otto schrieb in Beitrag Nr. 2282-11:Mein Fazit heute:
Die Formeln kann man so nicht gleich setzen, weil die Gleichung für die Fluchtgeschwindigkeit den relativistischen Anteil nicht berücksichtigt (Faktor 1/(1-rs⁄r) .
In der Gleichung für die Fluchtgeschwindigkeit muss man den Faktor 1/(1-rs⁄r) m.E. nicht berücksichtigen, weil hier nicht der Abstand vom Gravitationszentrum r sondern die bewegte Probemasse m relativistisch zu behandeln wäre. Die Fluchtgeschwindigkeit ist aber von der Probemasse unabhängig, weil sie auf beiden Seiten der Gleichung
Otto schrieb in Beitrag Nr. 2282-1:0,5∙m∙v² = G∙M∙m/r .
auftaucht, sich deren Einfluss also herauskürzt.
In der resultierenden Gleichung v2 = 2 GM/r "setzt" man dann rs definitionsgemäß als denjenigen Abstand, bei dem die Fluchtgeschwindigkeit die Lichtgeschwindigkeit erreicht.
[Gäste dürfen nur lesen]
| Beiträge: 340, Mitglied seit 6 Jahren |
Beitrag Nr. 2282-13
02.11.2017 16:39
|
Irgendwie sehe ich nicht, dass die beiden Formeln identisch sind, es sei denn, rs ist 2r/m. Bei v=c erhalte ich beim 1. v²=2GM/rs und beim 2. das selbe, wie es schon da steht. Insgesamt also GMm/r=2GM/rsOtto schrieb in Beitrag Nr. 2282-1:Der Schwarzschildradius berechnet sich zu
rs = 2∙G∙M /c²
Setzt man hier c = v, dann erhält man
v² = G∙M∙m /r (1)
...
Ist die Identität beider Gleichungen wirklich Zufall, wie immer zu lesen ist?
Habt Ihr andere Ideen, warum diese Gleichungen identisch sein könnten?
...
Darüber hinaus wird der Linke Teil der 2. Formel zu einer Radialbeschleunigung und der rechte zum rechten Teil des Gravitationsgesetzes, wenn man beide Seiten durch r teilt. Der Rechte Teil des Gravitationsgesetzes soll aber eine Kraft ergeben und keine Beschleunigung. GMm/r hingegen ergibt allenfalls eine Energie (Nm), wie auch v²m/2. Und wenn v²m/2=GMm/r gelten würde, würde auch v²=2GM/r passen. Versteh' ich hier nur was falsch oder passt hier an den Formeln tatsächlich etwas nicht?
Signatur:
Stay critical and keep thinking
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2282-14
02.11.2017 18:41
|
Hallo "Nicht von Bedeutung",
willkommen im Forum!
Ich denke inzwischen, daß ich bei der Suche nach einer Erklärung meiner ursprünglichen Frage eigentlich auf dem Holzwege bin.
Deshalb lassen sich die Formeln auch nicht richtig erklären und begründen.
Die Fluchtgeschwindigkeit in der klassischen Physik ergibt sich auf Basis der potentiellen Energie eines Gravitationsfeldes.
Die potentielle Energie ist die Fähigkeit, aus der Gravitationskraft des Feldes einer Masse Energie zu gewinnen. Diese Energie wird umgesetzt, wenn man eine kleine Masse im Gravitationsfeld einer großen Masse bewegt (zur großen Masse hin oder von der großen Masse weg).
„Die Fluchtgeschwindigkeit einer kleinen Masse aus dem Gravitationsfeld einer großen Masse ist ein Maß dafür, wie viel Energie die kleine Masse beim freien Fall aus dem Unendlichen auf die große Masse aufnimmt. Die Fluchtgeschwindigkeit ist betragsgleich der Fallgeschwindigkeit, nur die Richtung ist entgegengesetzt. Fall- und Fluchtgeschwindigkeit sind unabhängig von der Größe und der Struktur der kleinen Masse.“
Zitat aus http://www.altenbrunn.de/FLUCHT.pdf
Für den Fall einer relativistischen Betrachtungsweise kann die potentielle Energie bei der Annäherung einer kleinen Masse aus dem Unendlichen bis zum Radius r mit der relativistischen Bewegungsenergie gleichgesetzt werden.
Berechnungen auf diesen beiden Grundsätzen für eine relativistische und auch nicht-relativistische Fluchtgeschwindigkeit kommen (für beide Fälle) zu der Beziehung
v = c∙sqrt(rs/r)
Auf Einzelheiten siehe obigen Link.
Diese Gleichung ist die Fluchtgeschwindigkeit einer beliebigen kleinen Masse aus dem Schwerefeld einer beliebigen großen Masse mit endlicher Dichte.
Der Wert von v liegt immer zwischen 0 und c. Die Fluchtgeschwindigkeit wird nirgendwo unendlich oder größer als die Lichtgeschwindigkeit.Traue nie Deinen Sinnen.
willkommen im Forum!
Nicht von Bedeutung schrieb in Beitrag Nr. 2282-13:Versteh' ich hier nur was falsch oder passt hier an den Formeln tatsächlich etwas nicht?
Ich denke inzwischen, daß ich bei der Suche nach einer Erklärung meiner ursprünglichen Frage eigentlich auf dem Holzwege bin.
Deshalb lassen sich die Formeln auch nicht richtig erklären und begründen.
Die Fluchtgeschwindigkeit in der klassischen Physik ergibt sich auf Basis der potentiellen Energie eines Gravitationsfeldes.
Die potentielle Energie ist die Fähigkeit, aus der Gravitationskraft des Feldes einer Masse Energie zu gewinnen. Diese Energie wird umgesetzt, wenn man eine kleine Masse im Gravitationsfeld einer großen Masse bewegt (zur großen Masse hin oder von der großen Masse weg).
„Die Fluchtgeschwindigkeit einer kleinen Masse aus dem Gravitationsfeld einer großen Masse ist ein Maß dafür, wie viel Energie die kleine Masse beim freien Fall aus dem Unendlichen auf die große Masse aufnimmt. Die Fluchtgeschwindigkeit ist betragsgleich der Fallgeschwindigkeit, nur die Richtung ist entgegengesetzt. Fall- und Fluchtgeschwindigkeit sind unabhängig von der Größe und der Struktur der kleinen Masse.“
Zitat aus http://www.altenbrunn.de/FLUCHT.pdf
Für den Fall einer relativistischen Betrachtungsweise kann die potentielle Energie bei der Annäherung einer kleinen Masse aus dem Unendlichen bis zum Radius r mit der relativistischen Bewegungsenergie gleichgesetzt werden.
Berechnungen auf diesen beiden Grundsätzen für eine relativistische und auch nicht-relativistische Fluchtgeschwindigkeit kommen (für beide Fälle) zu der Beziehung
Auf Einzelheiten siehe obigen Link.
Diese Gleichung ist die Fluchtgeschwindigkeit einer beliebigen kleinen Masse aus dem Schwerefeld einer beliebigen großen Masse mit endlicher Dichte.
Der Wert von v liegt immer zwischen 0 und c. Die Fluchtgeschwindigkeit wird nirgendwo unendlich oder größer als die Lichtgeschwindigkeit.
Signatur:
Beitrag zuletzt bearbeitet von Otto am 02.11.2017 um 18:47 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2282-15
02.11.2017 22:15
|
Nicht von Bedeutung schrieb in Beitrag Nr. 2282-13:Irgendwie sehe ich nicht, dass die beiden Formeln identisch sind, es sei denn, rs ist 2r/m. Bei v=c erhalte ich beim 1. v²=2GM/rs und beim 2. das selbe, wie es schon da steht. Insgesamt also GMm/r=2GM/rs
Hallo "Nicht von Bedeutung",
entschuldige, ich habe vergessen, auf den ersten Teil Deines Beitrages einzugehen.
Natürlich hast Du recht mit meinem Schreibfehler.
Richtig ist v² = 2GM/r (anstelle v² = GMm/r).
Danke für den Hinweis.
Otto
P.S. Die aus der klassischen Physik bekannte Fluchtgeschwindigkeit basiert auf der Gleichheit von kinetischer Energie einer Masse "m" mit der Bindungsenergie des Gravitationsfeldes infolge der Masse "M" und beschreibt den Punkt des Verlassens des Gravitationsfeldes.
0,5∙m∙v² = G∙M∙m/r
v² = 2GM/r
Die kleinere Masse 'm' auf beiden Seiten kürzt sich raus.
Signatur:
[Gäste dürfen nur lesen]
| Beiträge: 340, Mitglied seit 6 Jahren |
Beitrag Nr. 2282-16
03.11.2017 01:30
|
Hallo Otto
Nichts zu Danken. Schön, dass ich helfen konnte.
Ich muss zugeben, dass mir Schwarzschildradius und Fluchtgeschwindigkeit nicht wirklich geläufig sind, "fehlerhaft" umgestellte Formeln aber schon. Allerdings habe ich auch schon mal erlebt, dass man einzelne Faktoren bei Herleitungen auch gerne mal vernachlässigt, weil extrem klein oder eben 0, wie z.B. das x² bei der Herleitung der Radialbeschleunigung über Aristoteles (v²t²=2rx+x² -> v²t²=2rx; Quelle: https://youtu.be/SeORz7UV2wI?t=6m26s). Deswegen hätte es ja sein können, dass hier Ähnliches greift.Ich versteh' zwar nicht, was du sagst, aber das kann nur daran liegen, dass du nicht verstehst, was es bedeutet.
Stay critical and keep thinking
Nichts zu Danken. Schön, dass ich helfen konnte.
Ich muss zugeben, dass mir Schwarzschildradius und Fluchtgeschwindigkeit nicht wirklich geläufig sind, "fehlerhaft" umgestellte Formeln aber schon. Allerdings habe ich auch schon mal erlebt, dass man einzelne Faktoren bei Herleitungen auch gerne mal vernachlässigt, weil extrem klein oder eben 0, wie z.B. das x² bei der Herleitung der Radialbeschleunigung über Aristoteles (v²t²=2rx+x² -> v²t²=2rx; Quelle: https://youtu.be/SeORz7UV2wI?t=6m26s). Deswegen hätte es ja sein können, dass hier Ähnliches greift.
Signatur:
Stay critical and keep thinking
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2282-17
03.11.2017 05:07
|
Hallo "Nicht von Bedeutung" ,
Die Richtigkeit der Gleichung von J. Altmann läßt sich einfach prüfen.
Mit dieser Fluchtgeschwindigkeit v² = (rs/r) c²∙
und der Gleichung des Schwarzschildradius v² = c² = 2GM/r
wird (rs/r) c²∙= 2GM/r
also rs = 2GM/c²
Nun ist Mꞌ = GM/c² (siehe mein Beitrag Nr. 2282-4) und damit wird rs = 2Mꞌ.
q.e.d.Traue nie Deinen Sinnen.
Ja das ist sinnvoll, um zu einfach handhabbaren Gleichungen mit genügender Genauigkeit zu kommen.Nicht von Bedeutung schrieb in Beitrag Nr. 2282-16:Allerdings habe ich auch schon mal erlebt, dass man einzelne Faktoren bei Herleitungen auch gerne mal vernachlässigt, weil extrem klein oder eben 0, ...
Das wäre ja noch zu beweisen.Nicht von Bedeutung schrieb in Beitrag Nr. 2282-16:... "fehlerhaft" umgestellte Formeln ...
Die Richtigkeit der Gleichung von J. Altmann läßt sich einfach prüfen.
Mit dieser Fluchtgeschwindigkeit v² = (rs/r) c²∙
und der Gleichung des Schwarzschildradius v² = c² = 2GM/r
wird (rs/r) c²∙= 2GM/r
also rs = 2GM/c²
Nun ist Mꞌ = GM/c² (siehe mein Beitrag Nr. 2282-4) und damit wird rs = 2Mꞌ.
q.e.d.
Signatur:
[Gäste dürfen nur lesen]
| Beiträge: 340, Mitglied seit 6 Jahren |
Beitrag Nr. 2282-18
03.11.2017 05:40
|
Haha... nö. Wir (bzw. ich) haben doch schon bewiesen, dass deine Formel im Ersten Beitrag fehlerhaft umgestellt war, sonst hättest du es ja nicht verbessert. ;)Otto schrieb in Beitrag Nr. 2282-17:Das wäre ja noch zu beweisen.
Und wo wir grade dabei sind:
Müsste es nicht "und der Gleichung des Schwarzschildradius v²=(rs/r)c²=2GM/r" heissen?
Naja... so lerne ich wenigstens etwas über Fluchtgeschwindigkeiten und Schwarzschildradien.
Signatur:
Stay critical and keep thinking
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2282-19
03.11.2017 09:21
|
Jetzt ja. Das war ja des Pudels Kern.Nicht von Bedeutung schrieb in Beitrag Nr. 2282-18:Müsste es nicht "und der Gleichung des Schwarzschildradius v²=(rs/r)c²=2GM/r" heissen?
Meine Formulierung zielte auf die ursprüngliche Frage dieses Themas, Beitrag Nr. 2282-1.
Signatur:
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2282-20
04.11.2017 06:02
|
Otto schrieb in Beitrag Nr. 2282-19:Das war ja des Pudels Kern.
Ich denke, diese kurze Formulierung bedarf zum besseren Verständnis eine Erläuterung, um die im Beitrag Nr. 2282-1 ursprünglich aufgeworfenen Frage zu beantworten.
Es ist nicht richtig, die Lichtgeschwindigkeit c einfach durch v zu ersetzen, weil die Relativgeschwindigkeit v eine Funktion darstellt, während der Wert c eine Konstante ist.
Die Gleichung für die Fluchtgeschwindigkeit wird erst dann richtig, wenn der Wert c durch die Gleichung c = v∙sqrt(r/rs) ersetzt wird.
Die Fluchtgeschwindigkeit v ist keine Konstante, sondern eine Funktion des Verhältnisses Schwarzschildradius zu Distanz (rs/r)
v² = (rs/r) c²∙
Siehe http://www.altenbrunn.de/FLUCHT.pdf
Richtig wäre also zu schreiben
(rs/r) c²∙= 2GM/r
anstelle von v²=2GM/r
Signatur:
Beitrag zuletzt bearbeitet von Otto am 04.11.2017 um 06:22 Uhr.
[Gäste dürfen nur lesen]
In diesem Forum dürfen nur Mitglieder schreiben. Hier kannst du dich anmelden


 Nach oben
Nach oben