Arbeitsplattform SRT
Thema erstellt von Bauhof
| Beiträge: 1.375, Mitglied seit 16 Jahren |
Beitrag Nr. 1991-1
21.01.2013 15:20
|
Hallo zusammen,
bitte hier keine Beiträge einstellen!
Warum? Es soll nur der erste Beitrag hier verbleiben, den ich immer auf den neuesten Stand nach Absprache mit Zara.t. bringe. Er soll eine Wissensplattform zur SRT für alle werden, damit jeder darauf zurückgreifen kann, wenn Fragen entstehen. Hier eingehende Beiträge werden weder von mir noch von Zara.t. beantwortet.
Wenn ihr darüber diskutieren möchtet, dann bitte im Thread Basics spezielle Relativitätstheorie! Vielen Dank im Voraus.
M.f.G. Eugen Bauhof
Forenteilnehmer, deren Beiträge bis jetzt hier eingebracht wurden (in alphabetischer Reihenfolge):
Bauhof, Grtgrt, Henry, Okotombrok, Zara.t.
Themen, die demnächst in den SRT-Basics diskutiert werden sollen:
(A) Begriff des Beobachtens.
(B) Maxwellsche Gleichungen.
(C) E = mc².
(D) Die Lorentz-Transformationen, hergeleitet allein aus dem Relativitätsprinzip.
(E) Transformationen, die das Linienelement ds² = (c dt)² - dx² - dy² - dz² invariant lassen.
Arbeitsplattform SRT
Inertialsysteme
1. Verschiedene Inertialsysteme bewegen sich gegeneinander geradlinig und gleichförmig. Alle Inertialsysteme bewegen sich relativ zueinander mit einer Geschwindigkeit v<c.
2. Sich drehende oder anderweitig beschleunigte Bezugssysteme sind keine Inertialsysteme.
3. Auch gleichförmig beschleunigte Systeme sind keine Inertialsysteme. Eine gleichförmige Beschleunigung ist keine gleichförmige Bewegung und somit nicht der Ruhe äquivalent.
4. Ein Teilchen, das sich mit Lichtgeschwindigkeit bewegt, hat keine Ruhemasse. Deshalb gibt es kein Inertialsystem, in dem Photonen in Ruhe wären.
5. Ein System, in dem sich jeder kräftefreie Körper gleichförmig geradlinig bewegt, wird als Inertialsystem bezeichnet.
6. Das Zusammentreffen von Kräftefreiheit und gleichförmiger Geradlinigkeit sämtlicher Bewegungen gibt es nur in Inertialsystemen.
7. Es kann kein Inertialsystem geben, das sich relativ zu einem zweiten Inertialsystem mit c bewegt. Grund: alle lichtartigen Weltlinien haben die Länge Null.
8. Wenn ein Lichtstrahl im Koordinatenursprung O(0,0,0) startet. dann gilt:
S² = (ct)² - x² - y² - z² ; für Licht gilt: x² + y² + z² = (ct)² ==> S² = (ct)² - (ct)² = 0; S = 0
Wichtig: S ist für alle (also auch für die nicht lichtartigen) Weltlinien invariant unter Lorentztransformationen. Das heißt: die Eigenzeit eines Systems ist eine absolute Größe, sie ist die Zeit, die eine mit diesem System fest verbundene Borduhr anzeigt.
Relativitätsprinzip
1. Die Gesetze, nach denen sich die Zustände der physikalischen Systeme ändern, sind unabhängig davon, auf welches von zwei relativ zueinander in gleichförmiger Translationsbewegung befindlichen Koordinatensystemen diese Zustandsänderungen bezogen werden.
2. Alle Inertialsysteme sind gleichberechtigt, wenn es gilt Naturgesetze zu formulieren. Naturgesetze müssen kovariant formuliert werden können.
3. Alle Beobachter, die sich mit gleichförmiger Geschwindigkeit relativ zueinander bewegen, sind gleichermaßen zu der Behauptung berechtigt, sie befinden sich in Ruhe.
Absolute Ruhe
Die Physik kennt keine absolute Ruhe. Die Gesetze der Physik lauten in allen Inertialsystemen gleich und zeichnen keines aus (Relativitätsprinzip). Es gibt nur relative Ruhe, Ruhe in bezug auf ein spezielles Inertialsystem, das momentane Ruhsystem.
Absolutgeschwindigkeit
Mit keinem Experiment kann eine Absolutgeschwindigkeit eines Inertialsystems bestimmt werden; kein Experiment lässt die Unterscheidung von Ruhe und gleichförmiger Bewegung zu. Damit war auch das vor Einstein der als absolut ruhendes Lichtwellen-Trägermedium angesehene “Lichtäther" gegenstandslos, den “Lichtäther" gibt es nicht.
Beobachten
Unter Beobachten versteht man die Feststellung der Koordinaten von Ereignissen in einem Inertialsystem. Wenn man das wirkliche Beobachten meint, muss man die endliche Laufzeit des Lichtsignals vom Gegenstand zum Betrachter berücksichtigen.
Den Begriff des Beobachtens möchte Zara.t. noch diskutieren. Er ist von zentraler Wichtigkeit um das Denken und die Arbeitsweise Einsteins zu verstehen.
Lichtgeschwindigkeit
1. Die Lichtgeschwindigkeit ist eine physikalische Naturkonstante und hat einen exakt definierten Wert.
2. Man kann c=1 setzen. Um hier im Forum Missverständnisse zu vermeiden, wird folgendes vereinbart:
Lichtgeschwindigkeit im Vakuum (im SI-System): c = 299 792 458 m/s
3. Die Existenz einer invarianten Grenzgeschwindigkeit folgt aus dem Relativitätsprinzip. Der Wert dieser Grenzgeschwindigkeit wird von den Maxwellschen Gleichungen festgelegt und durch alle Messungen bisher bestätigt.
4. Aus den Maxwellschen Gleichungen ergibt sich die Ausbreitungsgeschwindigkeit c elektromagnetischer Wellen aus zwei experimentell herausgefundenen Konstanten:
c = 1/sqrt(µ0 • ε0)
µ0 = magnetische Feldkonstante.
ε0 = elektrische Feldkonstante.
Eigenzeit einer Uhr
Die Eigenzeit einer Uhr entspricht immer der Länge ihrer Weltlinie.
Länge der Weltlinie eines bewegten Objekts
Die Länge der Weltlinie eines ruhenden Objekts (keine Änderung der Ortskoordinaten) ist die abgelaufene Zeit. Das bleibt auch bei einer Bewegung des Objekts so, wir müssen uns nur darauf beschränken, wieder nur die Uhr abzulesen, die das Objekt unmittelbar begleitet. Dieses Zeitmaß heißt Eigenzeit... Der Ablauf der Eigenzeit wird nun nicht mehr nur von der Änderung der Zeitkoordinate, sondern auch von der Änderung der Ortskoordinate bestimmt.
Maxwellsche Gleichungen
Die Maxwellschen Gleichungen sagen in einfachen Worten: Die Änderung eines elektrischen Feldes induziert ein magnetisches Feld, die Änderung des magnetischen Feldes induziert ein elektrisches Feld, das sich ändernde elektische Feld induziert ein Magnetfeld, usw....dieser ständige Wechsel breitet sich wellenförmig mit c (im Vakuum) aus. Die Maxwellschen Gleichungen sind früher als die SRT unabhängig von der SRT entstanden. An ihrem Beispiel könnten wir zeigen, was eine kovariante Formulierung ist. So wie Maxwell seine Gleichungen formulierte, waren sie nämlich noch nicht kovariant. Man kann ihnen aber eine kovariante Form verpassen.
Energie-Impuls-Beziehung
Die Energie-Impuls-Beziehung ist eine invariante Größe:
E² – (pc)² = (mc²)² || = constant
E..................Gesamtenergie, sie ist bezugssystemabhängig.
p...................Impuls, er ist bezugssystemabhängig.
mc²:=E0.......Ruheenergie sie ist bezugssystemunabhängig.
Nachdem die Ruheenergie bezugssystemunabhängig ist, ist auch die Masse m invariant.
SRT-Glossar
Äther
Ein Medium, in dem sich Licht und andere elektromagnetische Wellen fortpflanzen sollten. Diese Vorstellung wurde, vor allem nach der Entdeckung der Speziellen Relativitätstheorie, durch eine Feldbeschreibung ersetzt, nach der sich elektromagnetische Wellen auch ohne jedes Medium im leeren Raum fortpflanzen können. Die Vorstellung vom Äther wurde durch die Relativitätstheorie widerlegt.
Beobachter
Idealisierte Person oder Apparatur, oft hypothetischer Natur, die relevante Eigenschaften eines physikalischen Systems misst. Jeder Beobachter, der sich inertial bewegt, darf annehmen, dass er selbst in Ruhe sei. Er beobachtet lediglich, dass alle anderen Beobachter sich relativ zu ihm bewegen oder in Ruhe sind. Mehr kann er nicht beobachten, insbesondere kann er keine Eigenbewegung aus den Bewegungen anderer ableiten. Für ihn sieht es so aus, als würde er ruhen und alle anderen Beobachter bewegen sich.
Beschleuniger
Ein Instrument, das die Geschwindigkeit, und damit die Energie, geladener Teilchen erhöht. Beschleunigt werden können stabile Teilchen wie Elektron, Proton und Ionen.
Beschleunigung
Eine Veränderung der Geschwindigkeit, das heißt des Geschwindigkeitsbetrags und/oder der Bewegungsrichtung eines Objekts.
Bezugssystem
Die räumliche Beschreibung von Vorgängen braucht ein Bezugssystem (Koordinatensystem, Koordinaten) In einem Bezugssystem kann man die Bewegung eines Körpers beschreiben, ebenso aber auch die Bewegung eines anderen Bezugsystems, z. B. eine gradlinig gleichförmige Bewegung eines Bezugssystems in einem anderen, oder auch eine Drehung, eine krummlinige Bewegung oder eine beliebige Beschleunigung. Die Spezielle Relativitätstheorie diskutiert die Frage, wie sich zwei Beschreibungen desselben Vorgangs zueinander verhalten, die zu Bezugssystemen gehören die gegeneinander gleichförmig bewegt sind. Alle Bezugsysteme, die sich relativ zu einem Inertialsystem gleichförmig und geradlinig bewegen, sind ebenfalls Inertialsysteme.
Dilatation
Das Auseinanderziehen, die Verlängerung. Hier gebraucht im Zusammenhang mit Zeitdilatation, d.h. die Verlängerung der Zeiten in einem bewegten System gemäß der Speziellen Relativitätstheorie.
Doppler-Effekt-Verschiebung
Verschiebung der Spektrallinien einer Strahlung durch die Bewegung ihrer Quelle relativ zur Sichtlinie. Annäherung verursacht Blauverschiebung, Entfernung Rotverschiebung.
Eigenzeit
Eigenzeit ist die Zeit, gemessen von einer Uhr, welche die Bewegung eines Beobachters mitmacht. Uhren in relativer Bewegung zu einem Beobachter messen, dass seine und die Eigenzeit verschieden schnell vergehen. Die Länge der Weltlinie eines ruhenden Objekts (keine Änderung der Ortskoordinaten) ist die abgelaufene Zeit. Das bleibt auch bei einer Bewegung des Objekts so, wir müssen uns nur darauf beschränken, wieder nur die Uhr abzulesen, die das Objekt unmittelbar begleitet. Dieses Zeitmaß heißt Eigenzeit. Der Ablauf der Eigenzeit wird nun nicht mehr nur von der Änderung der Zeitkoordinate, sondern auch von der Änderung der Ortskoordinate bestimmt.
Elektrodynamik
Theorie der elektrischen und magnetischen Erscheinungen, zusammengefasst in der einheitlichen Elektrodynamik am Ende des 19. Jahrhunderts durch Maxwell. Dazu gehört vor allem die Theorie der elektromagnetischen Wellen, wie z. b. Radiowellen, Licht oder Gammastrahlen.
Elektromagnetische Welle
Eine wellenartige Störung in einem elektromagnetischen Feld. Alle diese Wellen breiten sich mit Lichtgeschwindigkeit aus. Sichtbares Licht, Röntgenstrahlen, Mikrowellen und Infrarotstrahlung sind Beispiele dafür.
Energie
Physikalische Grundgroße, für die ein strenger Erhaltungssatz gilt. Sie kann verschiedene Formen annehmen, z. B. die potentielle Energie eines im Schwerefeld hochgehobenen Gewichts, die kinetische Energie eines bewegten Körpers, die Wärmeenergie, in die schließlich jede Energie anderer Formen übergeht, oder die als Masse vorhandene Energie gemäß der Speziellen Relativitätstheorie. („Trägheit der Energie")
Ereignis
Ein Weltpunkt in der Raumzeit. Beschrieben durch vier Koordinaten: {x, y, z. t}.
Frequenz
Die Zahl vollständiger Wellenzyklen, die eine Welle pro Zeiteinheit durchläuft.
Grobes Missverständnis der SRT.
Etliche Kritiker der SRT in den letzten 100 Jahren glaubten, die relativistische Zeitdilatation sei ein rein "perspektivischer" Beobachtungs-Effekt und allein durch die Lichtlaufzeiten zum Beobachter zu erklären. Ein ganz grobes Missverständnis der SRT.
Geschwindigkeit
Der Geschwindigkeitsbetrag und die Bewegungsrichtung eines Objekts, zu einer Größe zusammengefasst. Die Geschwindigkeit ist differentiell definiert als Ortsänderung pro Zeiteinheit.: v = dx/dt. Wenn eine punktförmige Lichtquelle angeschaltet wird, entsteht eine Kugelwelle, deren Radius sich mit 299 752 458 m/sec vergrößert. Ihr Durchmesser aber vergrößert sich doppelt so schnell. Das ist kein Widerspruch zur SRT, da die Rate, mit der sich ein Abstand vergrößert, nicht als Ortsveränderung eines physikalischen Objekts verstanden werden kann. Diese Vergrößerung des Durchmessers kann nicht mit der Einsteinschen Geschwindigkeitsadditions-Formel berechnet werden, weil es sich bei der Verdoppelung des Durchmessers nicht um eine Geschwindigkeit im Sinne der SRT handelt.
Gleichzeitigkeit
In der klassischen Mechanik ist die Gleichzeitigkeit von Ereignissen unabhängig von jedem Bewegungszustand und von der Entfernung definiert. In der speziellen Relativitätstheorie hängt die Definition der Gleichzeitigkeit von der Relativ-Geschwindigkeit und von der Entfernung ab (Einsteins Relativität der Gleichzeitigkeit).
Gleichzeitigkeits-Definition von Einstein
“Die für A und B gemeinsame Zeit kann so definiert werden, indem man durch Definition festsetzt, dass die Zeit, welche das Licht braucht, um von A nach B zu gelangen, gleich ist der Zeit, welche es braucht, um von B nach A zu gelangen.“
Für entfernte Punkte kann man zu einer Gleichzeitigkeits-Definition also überhaupt nur gelangen auf dem Wege eines konstruktiven Postulats, in dem gefordert wird, dass die Ausbreitung des Lichtes, gemessen in der noch zu definierenden gemeinsamen Zeit, ein Vorgang mit konstanter Geschwindigkeit ist. Dieses Postulat ist entscheidend an der Konstruktion des Begriffs der gemeinsamen Zeit beteiligt.
Ideale Uhren.
Zur Herleitung der Theorien (der SRT und der ART) legt man sogenannte "ideale" Uhren zugrunde. So eine ideale Uhr wird realisiert durch Atomuhren. Reale Experimente, welche die SRT belegen, werden mit den Taktraten von Atomuhren durchgeführt
Inertialsystem.
Ein Inertialsystem ist ein Bezugssystem, in dem sich kräftefreie Körper geradlinig gleichförmig bewegen. Das bedeutet, dass es sich bei einem Inertialsystem um ein nicht rotierendes und nicht beschleunigtes Bezugssystem handelt. Alle Bezugsysteme, die sich relativ zu einem Inertialsystem gleichförmig und geradlinig bewegen, sind ebenfalls Inertialsysteme. Somit bewegen sich Körper, auf die keine Kräfte wirken, in allen Inertialsystemen auf Geraden. Eine gleichförmige Rotationsbewegung wäre demzufolge nichtinertial. Jeder nichtrotierende Beobachter, der sich gleichförmig und unbeschleunigt bewegt, befindet sich in einem Inertialsystem. Auf ihn wirken keine Kräfte.
Es gibt kein ausgezeichnetes Inertialsystem, von dem man behaupten könnte, es sei absolut ruhend. Es gibt keinen Punkt im Universum, von dem man sagen könnte, das sei allein der "absolut ruhende Pol", auf dem man jede andere Bewegung beziehen könnte. Insbesondere gibt es auch keinen "absoluten Raum", auf dem man alle Bewegungen beziehen könnte. Sowohl in der klassischen Mechanik wie in der Speziellen Relativitätstheorie sind alle Inertialsysteme für die Beschreibung gleichberechtigt.
Isotropie
Unabhängigkeit von Richtung oder Winkel. In einem isotropen Universum sind sämtliche messbaren Größen in allen Richtungen gleich.
Invarianz
Die Unveränderlichkeit bestimmter Größen oder Beziehungen, auch wenn andere Charakteristika transformiert werden. Invarianz-Überlegungen der Physik beziehen sich gewöhnlich auf die Invarianz von Größen gegenüber Transformationsgruppen.
Invarianz der Lichtgeschwindigkeit.
Unter der Invarianz der der Lichtgeschwindigkeit versteht man z.B. folgendes: Für das Licht wird immer die gleiche Geschwindigkeit gemessen, unabhägig davon, ob sich die Lichtquelle auf uns zu- oder von uns fortbewegt. Das sehen alle Beobachter so, gleichgültig, ob sie auf der Lichtquelle sitzen oder ob sie sich außerhalb befinden und die Lichtquelle als bewegt wahrnehmen. Daraus folgt: Die Lichtgeschwindigkeit ist in allen Inertialsystemen gleich groß.
Kinematik der Relativitätstheorie
Die Grundlagen der Relativitätstheorie können durch geometrische Intuition erschlossen werden. Die Kinematik der Relativitätstheorie kann daher als die Geometrie der Raumzeit-Union angesehen werden.
Kinetische Energie
ist die mit der Bewegung verknüpfte Energie; sie ist gleich der Arbeit, die geleistet werden muss, um einen Körper der Masse m aus dem Ruhezustand in einen Bewegungszustand mit der Geschwindigkeit v zu bringen. Sie beträgt in der klassischen Mechanik 1/2•m•v2.
Konstanz der Lichtgeschwindigkeit
Darunter versteht man die Unabhängigkeit von der Ausbreitungsrichtung und die Unveränderlichkeit ihrer Größe bei Zusammensetzung.
Unabhängigkeit von der Ausbreitungsrichtung heißt zum Beispiel: Wenn ein Lichtstrahl senkrecht auf eine Spiegelfläche mit der Geschwindigkeit v=c trifft, dann hat auch der reflektierte Strahl die Geschwindigkeit v=c. Strahlen, die nicht senkrecht auftreffen, werden ebenfalls mit der Geschwindigkeit v=c reflektiert.
Kovariant
Die Beschreibung eines physikalischen Systems ist kovariant, wenn bei einer Transformation des Systems die transformierte Beschreibung des transformierten Systems dieselben Ergebnisse liefert wie die ursprüngliche Beschreibung des ursprünglichen Systems.
Lichtlaufzeiten.
Mit den Lichtlaufzeiten zum Beobachter sind die relativistischen Effekte nicht erklärbar. Das schließt nicht aus, dass man zum besseren Verstehen Gedankenexperimente macht, in denen die Lichtlaufzeiten mit einbezogen werden.
Lichtuhr
Eine hypothetische Uhr, welche die verstrichene Zeit misst, indem sie zählt, wie viele vollständige Rundreisen ein einzelnes Photon zwischen zwei Spiegeln zurücklegt.
Lorentz-Kontraktion
Man betrachte z.B. ein Raumschiff das von der Erde aus auf eine konstante Geschwindigkeit v beschleunigt wurde. Der auf der Erde zurückgebliebenen Beobachter wird im folgenden als ruhender Beobachter bezeichnet, der Beobachter im Raumschiff als Reisender.
Der Reisende stellt wie folgt eine Längenkontraktion der Strecke zwischen Start- und Zielpunkt fest: Anhand einer mitgeführten Uhr liest er die Zeitspanne ab, die vom Start-Zeitpunkt bis zum Ziel-Zeitpunkt verstrichen ist. Mit dieser sogenannten "Eigenzeit" berechnet er anhand seiner ihm bekannten Reisegeschwindigkeit eine verkürzte Reisestrecke.
Für den ruhenden Beobachter bleibt die Strecke zwischen Start- und Zielpunkt dagegen unverändert. Er stellt beim Reisenden nach dessen Rückkehr eine Zeitdilatation fest, d.h., dass die Uhr des Reisenden gegenüber seiner eigenen Uhr nachgegangen ist.
Minkowski-Raumzeit
Minkowski erkannte, dass die Kinematik der SRT graphisch darstellbar wird, wenn man neben den altbekannten kartesischen Koordinatenachsen x, y, z noch die vierte Achse ict einführt und sich bei der Veranschaulichung relativistischer Raum-Zeit-Verhältnisse auf jeweils zwei Achsen, typischerweise die Achsen x und ict, beschränkt. Für die Abstände zwischen Weltpunkten, die jetzt Raum- und Zeitkoordinaten hatten, galt die alte euklidische Regel quadrierter Koordinaten-Differenzen, allerdings mit einem durch i2 = ─1 veränderten Vorzeichen des zeitlichen Anteils:
ds2 = dx2 + dy2 + dz2 + d(ict)2
Die Lorentztransformationen konnten dann als Drehung in dieser vierdimensionalen Raumzeit verstanden werden, bei der diese Größe ds2 invariant blieb ebenso wie bei Drehung im dreidimensionalen Raum der dreidimensionale Abstand zweier Körper unverändert bleibt. Effekte wie die Lorentzkontraktion und die Zeitdilatation konnten nun als durch Projektion von Längen- und Zeitanteil von eigentlich längen- und zeitbehafteten Größen auf zueinander um den Winkel ß = arctan(v/c) gedrehte Koordinatenachsen anschaulich interpretiert werden.
Mittelpunkt im Universum.
Im Universum ist kein Ort feststellbar, der als Mittelpunkt im Universum bezeichnet werden könnte.
Newtonsche Bewegungsgesetze
Gesetze, welche die Bewegung von Körpern unter Kräfteeinfluss beschreiben, wobei sie voraussetzen, dass Raum und Zeit absolut und unwandelbar sind. Diese Gesetze galten unverändert, bis Einstein die spezielle Relativitätstheorie entdeckt hatte, die zeigt, dass die Newtonsche Theorie nur eine Näherung für den Grenzfall kleinerer Geschwindigkeiten ist.
Photon
Kleinstes Paket des elektromagnetischen Felds. Botenteilchen der elektromagnetischen Kraft. Kleinstes Lichtpaket.
Pseudoeuklidische Geometrie
Während in einem euklidischen Raum das Quadrat des Abstandes zweier verschiedener Punkte P1 und P2 stets größer als Null ist, kann es in der Minkowski-Welt auch kleiner oder gleich Null sein. Die Raumzeit-Union der Relativitätstheorie besitzt also keine euklidische Maßbestimmung. Vielmehr ist die Maßbestimmung die vierdimensionale Verallgemeinerung der pseudo-euklidischen Geometrie. Dies ist der mathematische Ausdruck dafür, dass die Zeitkoordinate eine andere Qualität als die 3 Raumkoordinaten besitzt.
Raum und Zeit als untrennbare Einheit.
Man kann die SRT nicht auf der Grundlage der klassischen Betrachtung mit Trennung von Raum und Zeit verstehen. Man kann die SRT erst dann verstehen, wenn man Raum und Zeit als untrennbare Einheit ansieht.
Raumzeit
Die drei physikalischen Dimensionen des Raums werden mit der Zeit, die als vierte Dimension aufgefasst wird, verknüpft und ergeben so das Raum-Zeit-Kontinuum, das den grundlegenden Rahmen in der Relativitätstheorie darstellt.
Relativgeschwindigkeit.
Jede Geschwindigkeit (eines Körpers oder eines Inertialsystems) ist immer nur eine Relativgeschwindigkeit.
Relativität der Bewegung
Relativ bedeutet, dass die Bewegung nur in Bezug auf ein anderes Objekt festgestellt werden kann. Die Relativität der Bewegung gleichförmig bewegter Objekte ist keine Entdeckung der SRT, sondern wurde bereits von Galileo erkannt.
Relativität der Gleichzeitigkeit.
Das ist die erste Konsequenz der Konstanz der Lichtgeschwindigkeit. Einstein argumentierte etwa wie folgt: Auch die Zeit ist relativ. Es gibt keine absolute Zeit, die für alle Inertialsysteme gültig ist. In jedem Inertialsystem läuft die Zeit anders ab, abhängig davon, wie schnell sich die Inertialsysteme relativ zueinander bewegen. Und das ist ein totaler Umsturz unseres Weltbildes, weil seit Newton die Zeit "überall gleich verfließt". Und genau das tut sie nicht.
Was für einen Beobachter gleichzeitig ist, ist für einen anderen bewegten Beobachter nicht gleichzeitig. Ob zwei räumlich getrennt liegende Ereignisse gleichzeitig sind oder nicht, kann nicht dadurch entschieden werden, dass man mit Hilfe einer Messung die Gleichzeitigkeit zweier Ereignisse feststellen könnte. Der Gleichzeitigkeits-Begriff getrennt liegender Ereignisse erlangt erst durch eine Definition seine Bestimmtheit. Gleichzeitigkeit ist objektiv unbestimmt.
Relativitätsprinzip
Zentraler Begriff der Relativitätstheorie, nach der die physikalischen Gesetze für alle Beobachter, die mit konstanter Geschwindigkeit relativ zueinander bewegt sind, die gleiche Form haben; daher ist jeder dieser Beobachter gleichermaßen zu der Behauptung berechtigt, er befinde sich in Ruhe. Dieses Prinzip wird in der allgemeinen Relativitätstheorie zum Äquivalenzprinzip erweitert. Bereits in der Newtonschen Mechanik waren alle Inertialsysteme gleichberechtigt. Die Newtonschen Axiome der Mechanik zeichnen kein Inertialsystem gegenüber dem anderen aus. Der Übergang von einem Inertialsystem in ein anderes Inertialsystem wird in der Newtonschen Mechanik durch eine Galilei-Transformation vollzogen.
Relativistischer Dopplereffekt
Der relativistische Dopplereffekt hängt nur von der Relativgeschwindigkeit von Sender und Empfänger ab.
Ruheenergie
ist die aus der Beziehung E0 = mc2 berechnete Energie , wobei m die Masse des Teilchens und c die Lichtgeschwindigkeit ist. Die Ruhenergie wird nur dann vollständig freigesetzt, wenn ein Teilchen mit seinem Antiteilchen zerstrahlt.
Ruhesystem.
Man kann sich als Beobachter in jedes beliebige Inertialsystem gedanklich hineinsetzen kann, um dieses Inertialsystem dann zum Ruhesystem zu erklären.
Spezielle Relativitätstheorie
Einsteins Gesetze von Raum und Zeit in Abwesenheit von Gravitation.
SRT als Sonderfall der ART
Die SRT lässt sich als Sonderfall der ART interpretieren, sie ist gültig für einen massefreien Raum. Bei einem masseerfüllten Raum lässt sich die SRT lokal näherungsweise anwenden.
Teilchenbeschleuniger
Anlage, die Teilchen fast auf Lichtgeschwindigkeit beschleunigt und sie dann mit anderen Teilchen zusammenstoßen lässt, um ihren materiellen Aufbau zu ermitteln.
Vektorraum
In der Mathematik eine Gesamtheit von Vektoren, d.h. Objekten, die sich addieren und mit Zahlen multiplizieren lassen. Vektorräume unterscheiden sich nach der Art dieser Zahlen (z. b. reelle oder komplexe Zahlen) und nach ihrer Dimensionszahl. Zum Beispiel bilden die möglichen Geschwindigkeiten im Raum einen dreidimensionalen reellen Vektorraum.
Vierdimensionaler Abstand zwischen zwei Ereignissen.
Für alle inertialen Beobachter ist der vierdimensionale Abstand zwischen zwei Ereignissen in der Raumzeit verbindlich. Alle messen den gleichen Wert. Man sagt, dieser Abstand ist das "Raumzeit-Intervall" und dieses ist invariant für alle Beobachter. Wenn man die zwei Raumdimensionen y und z weglässt und nur eine Raumdimension x und die Zeitdimension t betrachtet, dann ergibt sich das Raumzeit-Intervall s² zwischen zwei Ereignissen für zwei verschiedene Systeme wie folgt:
s² = (ct')² - (x')² = (ct)² - (x)².
Wellenlänge
Elektromagnetische Strahlung wird durch ihre Wellenlänge oder ihre Frequenz charakterisiert, deren Produkt gleich der Lichtgeschwindigkeit ist. Die Wellenlänge ist die Entfernung zwischen aufeinanderfolgenden Wellenfronten, und die Frequenz ist die Zahl der Wellenfronten, die an einen gegebenen Punkt in einer Sekunde vorbeilaufen. Im sichtbaren Bereich hat das Licht eine Wellenlänge von 400 bis 700 Nanometer und eine Frequenz von 7 x 1014 bis 4 X 1014 Hertz.
Weltlinie
Eine Abfolge von Weltpunkten.
Weltpunkt
Ein Ort in der Raumzeit. Er ist bestimmt durch vier Koordinaten: {x, y, z, t}
Zwillingsparadoxon.
Gegen Einsteins Zwillingsexperiment wird meist mit der Symmetrie der Zeitdilatation argumentiert:
Wenn Zwilling B einerseits die Uhr von Zwilling A langsamer gehen sieht, dann muss umgekehrt doch Zwilling A auch die Uhr von B langsamer gehen sehen. Das ist zwar richtig, gilt aber nur, solange sich Zwilling A und B jeweils in einem Inertialsystem bewegen. Doch Zwilling B muss umkehren, um zu A zurückkehren zu können, d. h., er beschleunigt und befindet sich daher nicht in einem Inertialsystem, im Gegensatz zu B.
Diese Antwort wiederum hat dazu geführt, dass oftmals die Beschleunigungsphasen von B für die Verjüngung verantwortlich gemacht werden. Aber auch das ist nicht richtig, wie sich leicht zeigen lässt, indem man aus dem Zwillingsparadoxon ein Drillingsparadoxon macht. In der nachstehenden Skizze sind die Weltlinien der Drillinge A, B und C dargestellt, wobei C identische Beschleunigungsphasen (gekrümmte Kurvenstücke, durchgezogen gezeichnet) durchläuft, allerdings ist seine Reise kürzer.
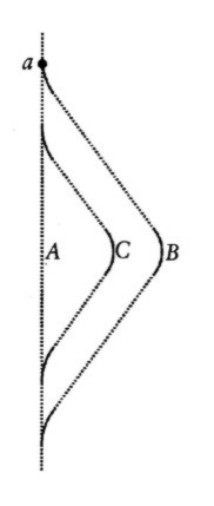
Nach Zusammenkunft aller drei ist A älter als C und C älter als B. Die Beschleunigungsphasen können also nicht für den Altersunterschied verantwortlich gemacht werden. Es ist die physikalische Geometrie der relativistischen Raumzeit: Der Weg von B ist kürzer als der von C, und dieser wiederum ist kürzer als der Weg von A.
Zwillingsexperiment als Quintessenz mehrerer Fach-Autoren.
1. Die Symmetrie der Zeitdilatation wird gebrochen, sobald der reisende Zwilling umkehrt.
2. Die Umkehr ist gleichbedeutend mit einem Inertialsystemwechsel.
3. Der Inertialsystemwechsel bei der Umkehr lässt die auf seiner Reise erarbeitete Zeitdilatation des reisenden Zwillings manifest werden.
4. Die verflossene Eigenzeit, die der jeweilige Zwilling auf seiner Uhr abliest, entspricht der jeweiligen Länge der Weltlinie im Minkowski-Raum.
5. Die Beschleunigungsphasen des reisenden Zwillings sind nicht die Ursache der Zeitdilatation. Man kann die Beschleunigungsphasen durch ein Differenzexperiment zum Verschwinden bringen. Die Zeitdilatation tritt dann trotzdem auf. Die Zeitdilatation ist im wesentlichen abhängig von der Reisedauer und der Reisegeschwindigkeit des reisenden Zwillings.
6. Manche meinen, dass nur die ART das scheinbare Paradoxon auflösen könnte, weil Beschleunigungen im Spiel sind. Mal ganz abgesehen davon, dass man mit der SRT auch Beschleunigungen beschreiben kann, ist die ART zu Auflösung des Zwillingsparadoxons nicht notwendig. Es kann allein mit Mitteln der SRT gelöst werden. Die ART wird nur dann benötigt, wenn die Gravitation ins Spiel kommt.
Herleitung der Lorentz-Transformationen mit Hilfe einer Koordinatensystemdrehung im Minkowski-Raum.
Zunächst wird die gewöhnliche Koordinatentransformation im euklidischen Raum in Skizze 1 dargestellt, so wie sie in jeder Formelsammlung zu finden ist:
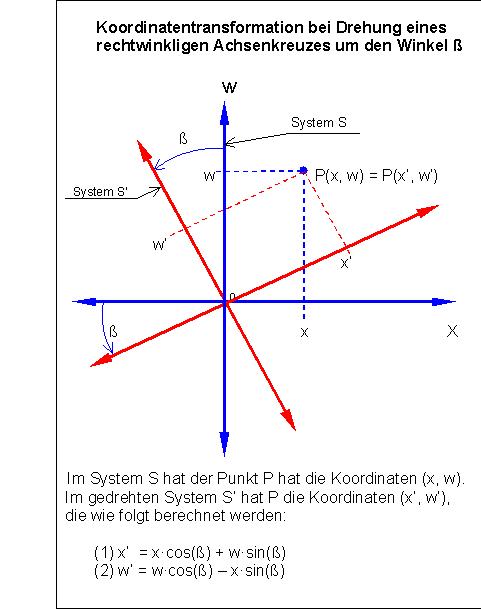
Skizze 1
Der Mathematiker Hermann Minkowski Minkowski ging von der Invarianz des Linienelementes aus und suchte allgemeine Transformationsgleichungen, die dies gewährleisten. Er hat dabei herausgefunden, dass allgemein jede Transformation zwischen relativ zueinander bewegten Inertialsystemen durch eine Koordinatensystemdrehung um einen imaginären Winkel in einem vierdimensionalen Raum darstellbar ist.
Gegeben sind zwei Inertialsysteme S und S', die sich relativ zueinander mit der Geschwindigkeit v bewegen. Ersetzt man w durch ict und ß durch den imaginären Winkel (iß), dann wird aus der reellen Drehung im euklidischen Raum eine imaginäre Drehung im Minkowski-Raum (x, w=ict). Die imaginäre Einheit in w=ict gewährleistet die pseudoeuklidische Metrik der Minkowski-Raumzeit.
Das ist vorläufig eine willkürliche mathematische Festsetzung ohne physikalische Begründung. Durch diese Festsetzung wird auch der Drehwinkel imaginär. Einstein stand ursprünglich den mathematischen Ideen Minkowskis zur SRT reserviert gegenüber: Er sagte: "Das bringt doch physikalisch nichts Neues!" Später erwies sich Minkowskis imaginärer Ansatz als sehr hilfreich zur späteren mathematischen Herleitung der ART-Gleichungen. Einsteins ursprüngliche Herleitung der ART-Gleichungen war nämlich sehr kompliziert und für einen mathematischen Laien nicht nachvollziehbar. Siehe Skizze 2:
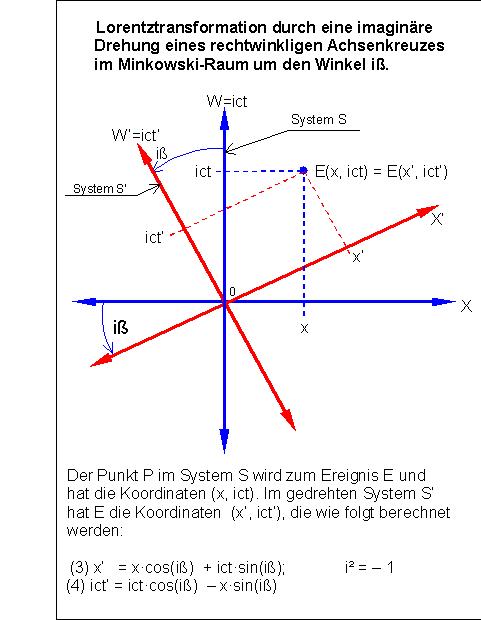
Skizze 2
Der Raumzeit-Abstand O-E bleibt durch die Drehung invariant. Das Ereignis E, das im System S durch den Weltpunkt E(x, ict) dargestellt wird, ist im System S’ der Weltpunkt E(x’, ict’). Bei dem Weltpunkt E handelt sich im System S und im System S’ um das gleiche Ereignis, nur die Koordinaten dieses Ereignisses haben im System S andere Werte als im System S’.
Die Transformationsgleichungen nehmen deshalb folgende Gestalt an:
(3) x' = x•cos(iß) + ict•sin(iß); i² = ─ 1
(4) ict' = ict•cos(iß) ─ x•sin(iß)
Zu jedem Zeitpunkt bewegt sich S' mit der Geschwindigkeit v = x/t in Richtung der positiven x-Achse; daraus folgt:
(5) x = v•t
Betrachtet man im 2. Quadranten des Systems S einen beliebigen Punkt (─ x, ict), der auf der auf der Ordinate w=ict' liegt, dann lässt sich für den Winkel (iß) der Tangens bestimmen:
(6) tan(iß) = ─ x/ict; mit x=v•t ergibt sich:
(7) tan(iß) = ─ v•t/ict
Für alle t ungleich Null ergibt sich:
(8) tan(iß) = ─ v/(ic); quadriert ergibt:
(9) tan²(iß) = ─ v²/c²
Der imaginäre Drehwinkel (iß) repräsentiert somit ─ über den Tangens dieses Winkels ─ die Relativgeschwindigkeit zwischen den beiden Inertialsystemen S und S' als Bruchteil der Lichtgeschwindigkeit. Aus einer Formelsammlung entnehme ich die Umformungen (10) und (11):
(10) sin(iß) = tan(iß)/sqrt[1 + tan²(iß)]
(11) cos(iß) = 1/sqrt[1 + tan²(iß)]
Mit der Kurzschreibweise G = 1/sqrt[1 + tan²(iß)] ergibt sich:
(12) sin(iß) = G•tan(iß)
(13) cos(iß) = G; (12) und (13) in (3) eingesetzt ergibt:
(14) x' = x•G + ict•G•tan(iß); mit tan(iß) = ─ v/(ic) ergibt sich:
(15) x' = x•G + ict•G•[─ v/(ic)]
(16) x' = x•G ─ t•G•v
(17) x' = G(x ─ v•t); aus (4) und (12) und (13) ergibt sich:
(18) ict' = ict•G ─ x•G•tan(iß); mit tan(iß) = ─ v/(ic) ergibt sich:
(19) ict' = ict•G ─ x•G•[ ─ v/(ic)]
(20) ict' = G[ ict ─ x•[ ─ v/(ic)] ]
(21) ict' = G[ict + x·v/(ic)]; dividiert durch (ic) ergibt:
(22) t' = G(t ─ x•v/c²)
Wenn man die Beziehung (9) in die Kurzschreibweise
G = 1/sqrt[1 + tan²(iß)] einsetzt, dann ergibt sich:
(23) G = 1/sqrt(1 ─ v²/c²)
Diese Gleichung in (17) und (22) eingesetzt ergeben die speziellen Lorentz-Transformationen:
x' = (x ─ v•t) / sqrt(1 ─ v²/c²)
t' = (t ─ v•x/c²) / sqrt(1 ─ v²/c²)
Neue Ergänzungen
13.12.2014 Lorentz-Kontraktion neu eingetragen.
bitte hier keine Beiträge einstellen!
Warum? Es soll nur der erste Beitrag hier verbleiben, den ich immer auf den neuesten Stand nach Absprache mit Zara.t. bringe. Er soll eine Wissensplattform zur SRT für alle werden, damit jeder darauf zurückgreifen kann, wenn Fragen entstehen. Hier eingehende Beiträge werden weder von mir noch von Zara.t. beantwortet.
Wenn ihr darüber diskutieren möchtet, dann bitte im Thread Basics spezielle Relativitätstheorie! Vielen Dank im Voraus.
M.f.G. Eugen Bauhof
Forenteilnehmer, deren Beiträge bis jetzt hier eingebracht wurden (in alphabetischer Reihenfolge):
Bauhof, Grtgrt, Henry, Okotombrok, Zara.t.
Themen, die demnächst in den SRT-Basics diskutiert werden sollen:
(A) Begriff des Beobachtens.
(B) Maxwellsche Gleichungen.
(C) E = mc².
(D) Die Lorentz-Transformationen, hergeleitet allein aus dem Relativitätsprinzip.
(E) Transformationen, die das Linienelement ds² = (c dt)² - dx² - dy² - dz² invariant lassen.
Inertialsysteme
1. Verschiedene Inertialsysteme bewegen sich gegeneinander geradlinig und gleichförmig. Alle Inertialsysteme bewegen sich relativ zueinander mit einer Geschwindigkeit v<c.
2. Sich drehende oder anderweitig beschleunigte Bezugssysteme sind keine Inertialsysteme.
3. Auch gleichförmig beschleunigte Systeme sind keine Inertialsysteme. Eine gleichförmige Beschleunigung ist keine gleichförmige Bewegung und somit nicht der Ruhe äquivalent.
4. Ein Teilchen, das sich mit Lichtgeschwindigkeit bewegt, hat keine Ruhemasse. Deshalb gibt es kein Inertialsystem, in dem Photonen in Ruhe wären.
5. Ein System, in dem sich jeder kräftefreie Körper gleichförmig geradlinig bewegt, wird als Inertialsystem bezeichnet.
6. Das Zusammentreffen von Kräftefreiheit und gleichförmiger Geradlinigkeit sämtlicher Bewegungen gibt es nur in Inertialsystemen.
7. Es kann kein Inertialsystem geben, das sich relativ zu einem zweiten Inertialsystem mit c bewegt. Grund: alle lichtartigen Weltlinien haben die Länge Null.
8. Wenn ein Lichtstrahl im Koordinatenursprung O(0,0,0) startet. dann gilt:
S² = (ct)² - x² - y² - z² ; für Licht gilt: x² + y² + z² = (ct)² ==> S² = (ct)² - (ct)² = 0; S = 0
Wichtig: S ist für alle (also auch für die nicht lichtartigen) Weltlinien invariant unter Lorentztransformationen. Das heißt: die Eigenzeit eines Systems ist eine absolute Größe, sie ist die Zeit, die eine mit diesem System fest verbundene Borduhr anzeigt.
Relativitätsprinzip
1. Die Gesetze, nach denen sich die Zustände der physikalischen Systeme ändern, sind unabhängig davon, auf welches von zwei relativ zueinander in gleichförmiger Translationsbewegung befindlichen Koordinatensystemen diese Zustandsänderungen bezogen werden.
2. Alle Inertialsysteme sind gleichberechtigt, wenn es gilt Naturgesetze zu formulieren. Naturgesetze müssen kovariant formuliert werden können.
3. Alle Beobachter, die sich mit gleichförmiger Geschwindigkeit relativ zueinander bewegen, sind gleichermaßen zu der Behauptung berechtigt, sie befinden sich in Ruhe.
Absolute Ruhe
Die Physik kennt keine absolute Ruhe. Die Gesetze der Physik lauten in allen Inertialsystemen gleich und zeichnen keines aus (Relativitätsprinzip). Es gibt nur relative Ruhe, Ruhe in bezug auf ein spezielles Inertialsystem, das momentane Ruhsystem.
Absolutgeschwindigkeit
Mit keinem Experiment kann eine Absolutgeschwindigkeit eines Inertialsystems bestimmt werden; kein Experiment lässt die Unterscheidung von Ruhe und gleichförmiger Bewegung zu. Damit war auch das vor Einstein der als absolut ruhendes Lichtwellen-Trägermedium angesehene “Lichtäther" gegenstandslos, den “Lichtäther" gibt es nicht.
Beobachten
Unter Beobachten versteht man die Feststellung der Koordinaten von Ereignissen in einem Inertialsystem. Wenn man das wirkliche Beobachten meint, muss man die endliche Laufzeit des Lichtsignals vom Gegenstand zum Betrachter berücksichtigen.
Den Begriff des Beobachtens möchte Zara.t. noch diskutieren. Er ist von zentraler Wichtigkeit um das Denken und die Arbeitsweise Einsteins zu verstehen.
Lichtgeschwindigkeit
1. Die Lichtgeschwindigkeit ist eine physikalische Naturkonstante und hat einen exakt definierten Wert.
2. Man kann c=1 setzen. Um hier im Forum Missverständnisse zu vermeiden, wird folgendes vereinbart:
3. Die Existenz einer invarianten Grenzgeschwindigkeit folgt aus dem Relativitätsprinzip. Der Wert dieser Grenzgeschwindigkeit wird von den Maxwellschen Gleichungen festgelegt und durch alle Messungen bisher bestätigt.
4. Aus den Maxwellschen Gleichungen ergibt sich die Ausbreitungsgeschwindigkeit c elektromagnetischer Wellen aus zwei experimentell herausgefundenen Konstanten:
c = 1/sqrt(µ0 • ε0)
µ0 = magnetische Feldkonstante.
ε0 = elektrische Feldkonstante.
Eigenzeit einer Uhr
Die Eigenzeit einer Uhr entspricht immer der Länge ihrer Weltlinie.
Länge der Weltlinie eines bewegten Objekts
Die Länge der Weltlinie eines ruhenden Objekts (keine Änderung der Ortskoordinaten) ist die abgelaufene Zeit. Das bleibt auch bei einer Bewegung des Objekts so, wir müssen uns nur darauf beschränken, wieder nur die Uhr abzulesen, die das Objekt unmittelbar begleitet. Dieses Zeitmaß heißt Eigenzeit... Der Ablauf der Eigenzeit wird nun nicht mehr nur von der Änderung der Zeitkoordinate, sondern auch von der Änderung der Ortskoordinate bestimmt.
Maxwellsche Gleichungen
Die Maxwellschen Gleichungen sagen in einfachen Worten: Die Änderung eines elektrischen Feldes induziert ein magnetisches Feld, die Änderung des magnetischen Feldes induziert ein elektrisches Feld, das sich ändernde elektische Feld induziert ein Magnetfeld, usw....dieser ständige Wechsel breitet sich wellenförmig mit c (im Vakuum) aus. Die Maxwellschen Gleichungen sind früher als die SRT unabhängig von der SRT entstanden. An ihrem Beispiel könnten wir zeigen, was eine kovariante Formulierung ist. So wie Maxwell seine Gleichungen formulierte, waren sie nämlich noch nicht kovariant. Man kann ihnen aber eine kovariante Form verpassen.
Energie-Impuls-Beziehung
Die Energie-Impuls-Beziehung ist eine invariante Größe:
E² – (pc)² = (mc²)² || = constant
E..................Gesamtenergie, sie ist bezugssystemabhängig.
p...................Impuls, er ist bezugssystemabhängig.
mc²:=E0.......Ruheenergie sie ist bezugssystemunabhängig.
Nachdem die Ruheenergie bezugssystemunabhängig ist, ist auch die Masse m invariant.
SRT-Glossar
Äther
Ein Medium, in dem sich Licht und andere elektromagnetische Wellen fortpflanzen sollten. Diese Vorstellung wurde, vor allem nach der Entdeckung der Speziellen Relativitätstheorie, durch eine Feldbeschreibung ersetzt, nach der sich elektromagnetische Wellen auch ohne jedes Medium im leeren Raum fortpflanzen können. Die Vorstellung vom Äther wurde durch die Relativitätstheorie widerlegt.
Beobachter
Idealisierte Person oder Apparatur, oft hypothetischer Natur, die relevante Eigenschaften eines physikalischen Systems misst. Jeder Beobachter, der sich inertial bewegt, darf annehmen, dass er selbst in Ruhe sei. Er beobachtet lediglich, dass alle anderen Beobachter sich relativ zu ihm bewegen oder in Ruhe sind. Mehr kann er nicht beobachten, insbesondere kann er keine Eigenbewegung aus den Bewegungen anderer ableiten. Für ihn sieht es so aus, als würde er ruhen und alle anderen Beobachter bewegen sich.
Beschleuniger
Ein Instrument, das die Geschwindigkeit, und damit die Energie, geladener Teilchen erhöht. Beschleunigt werden können stabile Teilchen wie Elektron, Proton und Ionen.
Beschleunigung
Eine Veränderung der Geschwindigkeit, das heißt des Geschwindigkeitsbetrags und/oder der Bewegungsrichtung eines Objekts.
Bezugssystem
Die räumliche Beschreibung von Vorgängen braucht ein Bezugssystem (Koordinatensystem, Koordinaten) In einem Bezugssystem kann man die Bewegung eines Körpers beschreiben, ebenso aber auch die Bewegung eines anderen Bezugsystems, z. B. eine gradlinig gleichförmige Bewegung eines Bezugssystems in einem anderen, oder auch eine Drehung, eine krummlinige Bewegung oder eine beliebige Beschleunigung. Die Spezielle Relativitätstheorie diskutiert die Frage, wie sich zwei Beschreibungen desselben Vorgangs zueinander verhalten, die zu Bezugssystemen gehören die gegeneinander gleichförmig bewegt sind. Alle Bezugsysteme, die sich relativ zu einem Inertialsystem gleichförmig und geradlinig bewegen, sind ebenfalls Inertialsysteme.
Dilatation
Das Auseinanderziehen, die Verlängerung. Hier gebraucht im Zusammenhang mit Zeitdilatation, d.h. die Verlängerung der Zeiten in einem bewegten System gemäß der Speziellen Relativitätstheorie.
Doppler-Effekt-Verschiebung
Verschiebung der Spektrallinien einer Strahlung durch die Bewegung ihrer Quelle relativ zur Sichtlinie. Annäherung verursacht Blauverschiebung, Entfernung Rotverschiebung.
Eigenzeit
Eigenzeit ist die Zeit, gemessen von einer Uhr, welche die Bewegung eines Beobachters mitmacht. Uhren in relativer Bewegung zu einem Beobachter messen, dass seine und die Eigenzeit verschieden schnell vergehen. Die Länge der Weltlinie eines ruhenden Objekts (keine Änderung der Ortskoordinaten) ist die abgelaufene Zeit. Das bleibt auch bei einer Bewegung des Objekts so, wir müssen uns nur darauf beschränken, wieder nur die Uhr abzulesen, die das Objekt unmittelbar begleitet. Dieses Zeitmaß heißt Eigenzeit. Der Ablauf der Eigenzeit wird nun nicht mehr nur von der Änderung der Zeitkoordinate, sondern auch von der Änderung der Ortskoordinate bestimmt.
Elektrodynamik
Theorie der elektrischen und magnetischen Erscheinungen, zusammengefasst in der einheitlichen Elektrodynamik am Ende des 19. Jahrhunderts durch Maxwell. Dazu gehört vor allem die Theorie der elektromagnetischen Wellen, wie z. b. Radiowellen, Licht oder Gammastrahlen.
Elektromagnetische Welle
Eine wellenartige Störung in einem elektromagnetischen Feld. Alle diese Wellen breiten sich mit Lichtgeschwindigkeit aus. Sichtbares Licht, Röntgenstrahlen, Mikrowellen und Infrarotstrahlung sind Beispiele dafür.
Energie
Physikalische Grundgroße, für die ein strenger Erhaltungssatz gilt. Sie kann verschiedene Formen annehmen, z. B. die potentielle Energie eines im Schwerefeld hochgehobenen Gewichts, die kinetische Energie eines bewegten Körpers, die Wärmeenergie, in die schließlich jede Energie anderer Formen übergeht, oder die als Masse vorhandene Energie gemäß der Speziellen Relativitätstheorie. („Trägheit der Energie")
Ereignis
Ein Weltpunkt in der Raumzeit. Beschrieben durch vier Koordinaten: {x, y, z. t}.
Frequenz
Die Zahl vollständiger Wellenzyklen, die eine Welle pro Zeiteinheit durchläuft.
Grobes Missverständnis der SRT.
Etliche Kritiker der SRT in den letzten 100 Jahren glaubten, die relativistische Zeitdilatation sei ein rein "perspektivischer" Beobachtungs-Effekt und allein durch die Lichtlaufzeiten zum Beobachter zu erklären. Ein ganz grobes Missverständnis der SRT.
Geschwindigkeit
Der Geschwindigkeitsbetrag und die Bewegungsrichtung eines Objekts, zu einer Größe zusammengefasst. Die Geschwindigkeit ist differentiell definiert als Ortsänderung pro Zeiteinheit.: v = dx/dt. Wenn eine punktförmige Lichtquelle angeschaltet wird, entsteht eine Kugelwelle, deren Radius sich mit 299 752 458 m/sec vergrößert. Ihr Durchmesser aber vergrößert sich doppelt so schnell. Das ist kein Widerspruch zur SRT, da die Rate, mit der sich ein Abstand vergrößert, nicht als Ortsveränderung eines physikalischen Objekts verstanden werden kann. Diese Vergrößerung des Durchmessers kann nicht mit der Einsteinschen Geschwindigkeitsadditions-Formel berechnet werden, weil es sich bei der Verdoppelung des Durchmessers nicht um eine Geschwindigkeit im Sinne der SRT handelt.
Gleichzeitigkeit
In der klassischen Mechanik ist die Gleichzeitigkeit von Ereignissen unabhängig von jedem Bewegungszustand und von der Entfernung definiert. In der speziellen Relativitätstheorie hängt die Definition der Gleichzeitigkeit von der Relativ-Geschwindigkeit und von der Entfernung ab (Einsteins Relativität der Gleichzeitigkeit).
Gleichzeitigkeits-Definition von Einstein
“Die für A und B gemeinsame Zeit kann so definiert werden, indem man durch Definition festsetzt, dass die Zeit, welche das Licht braucht, um von A nach B zu gelangen, gleich ist der Zeit, welche es braucht, um von B nach A zu gelangen.“
Für entfernte Punkte kann man zu einer Gleichzeitigkeits-Definition also überhaupt nur gelangen auf dem Wege eines konstruktiven Postulats, in dem gefordert wird, dass die Ausbreitung des Lichtes, gemessen in der noch zu definierenden gemeinsamen Zeit, ein Vorgang mit konstanter Geschwindigkeit ist. Dieses Postulat ist entscheidend an der Konstruktion des Begriffs der gemeinsamen Zeit beteiligt.
Ideale Uhren.
Zur Herleitung der Theorien (der SRT und der ART) legt man sogenannte "ideale" Uhren zugrunde. So eine ideale Uhr wird realisiert durch Atomuhren. Reale Experimente, welche die SRT belegen, werden mit den Taktraten von Atomuhren durchgeführt
Inertialsystem.
Ein Inertialsystem ist ein Bezugssystem, in dem sich kräftefreie Körper geradlinig gleichförmig bewegen. Das bedeutet, dass es sich bei einem Inertialsystem um ein nicht rotierendes und nicht beschleunigtes Bezugssystem handelt. Alle Bezugsysteme, die sich relativ zu einem Inertialsystem gleichförmig und geradlinig bewegen, sind ebenfalls Inertialsysteme. Somit bewegen sich Körper, auf die keine Kräfte wirken, in allen Inertialsystemen auf Geraden. Eine gleichförmige Rotationsbewegung wäre demzufolge nichtinertial. Jeder nichtrotierende Beobachter, der sich gleichförmig und unbeschleunigt bewegt, befindet sich in einem Inertialsystem. Auf ihn wirken keine Kräfte.
Es gibt kein ausgezeichnetes Inertialsystem, von dem man behaupten könnte, es sei absolut ruhend. Es gibt keinen Punkt im Universum, von dem man sagen könnte, das sei allein der "absolut ruhende Pol", auf dem man jede andere Bewegung beziehen könnte. Insbesondere gibt es auch keinen "absoluten Raum", auf dem man alle Bewegungen beziehen könnte. Sowohl in der klassischen Mechanik wie in der Speziellen Relativitätstheorie sind alle Inertialsysteme für die Beschreibung gleichberechtigt.
Isotropie
Unabhängigkeit von Richtung oder Winkel. In einem isotropen Universum sind sämtliche messbaren Größen in allen Richtungen gleich.
Invarianz
Die Unveränderlichkeit bestimmter Größen oder Beziehungen, auch wenn andere Charakteristika transformiert werden. Invarianz-Überlegungen der Physik beziehen sich gewöhnlich auf die Invarianz von Größen gegenüber Transformationsgruppen.
Invarianz der Lichtgeschwindigkeit.
Unter der Invarianz der der Lichtgeschwindigkeit versteht man z.B. folgendes: Für das Licht wird immer die gleiche Geschwindigkeit gemessen, unabhägig davon, ob sich die Lichtquelle auf uns zu- oder von uns fortbewegt. Das sehen alle Beobachter so, gleichgültig, ob sie auf der Lichtquelle sitzen oder ob sie sich außerhalb befinden und die Lichtquelle als bewegt wahrnehmen. Daraus folgt: Die Lichtgeschwindigkeit ist in allen Inertialsystemen gleich groß.
Kinematik der Relativitätstheorie
Die Grundlagen der Relativitätstheorie können durch geometrische Intuition erschlossen werden. Die Kinematik der Relativitätstheorie kann daher als die Geometrie der Raumzeit-Union angesehen werden.
Kinetische Energie
ist die mit der Bewegung verknüpfte Energie; sie ist gleich der Arbeit, die geleistet werden muss, um einen Körper der Masse m aus dem Ruhezustand in einen Bewegungszustand mit der Geschwindigkeit v zu bringen. Sie beträgt in der klassischen Mechanik 1/2•m•v2.
Konstanz der Lichtgeschwindigkeit
Darunter versteht man die Unabhängigkeit von der Ausbreitungsrichtung und die Unveränderlichkeit ihrer Größe bei Zusammensetzung.
Unabhängigkeit von der Ausbreitungsrichtung heißt zum Beispiel: Wenn ein Lichtstrahl senkrecht auf eine Spiegelfläche mit der Geschwindigkeit v=c trifft, dann hat auch der reflektierte Strahl die Geschwindigkeit v=c. Strahlen, die nicht senkrecht auftreffen, werden ebenfalls mit der Geschwindigkeit v=c reflektiert.
Kovariant
Die Beschreibung eines physikalischen Systems ist kovariant, wenn bei einer Transformation des Systems die transformierte Beschreibung des transformierten Systems dieselben Ergebnisse liefert wie die ursprüngliche Beschreibung des ursprünglichen Systems.
Lichtlaufzeiten.
Mit den Lichtlaufzeiten zum Beobachter sind die relativistischen Effekte nicht erklärbar. Das schließt nicht aus, dass man zum besseren Verstehen Gedankenexperimente macht, in denen die Lichtlaufzeiten mit einbezogen werden.
Lichtuhr
Eine hypothetische Uhr, welche die verstrichene Zeit misst, indem sie zählt, wie viele vollständige Rundreisen ein einzelnes Photon zwischen zwei Spiegeln zurücklegt.
Lorentz-Kontraktion
Man betrachte z.B. ein Raumschiff das von der Erde aus auf eine konstante Geschwindigkeit v beschleunigt wurde. Der auf der Erde zurückgebliebenen Beobachter wird im folgenden als ruhender Beobachter bezeichnet, der Beobachter im Raumschiff als Reisender.
Der Reisende stellt wie folgt eine Längenkontraktion der Strecke zwischen Start- und Zielpunkt fest: Anhand einer mitgeführten Uhr liest er die Zeitspanne ab, die vom Start-Zeitpunkt bis zum Ziel-Zeitpunkt verstrichen ist. Mit dieser sogenannten "Eigenzeit" berechnet er anhand seiner ihm bekannten Reisegeschwindigkeit eine verkürzte Reisestrecke.
Für den ruhenden Beobachter bleibt die Strecke zwischen Start- und Zielpunkt dagegen unverändert. Er stellt beim Reisenden nach dessen Rückkehr eine Zeitdilatation fest, d.h., dass die Uhr des Reisenden gegenüber seiner eigenen Uhr nachgegangen ist.
Minkowski-Raumzeit
Minkowski erkannte, dass die Kinematik der SRT graphisch darstellbar wird, wenn man neben den altbekannten kartesischen Koordinatenachsen x, y, z noch die vierte Achse ict einführt und sich bei der Veranschaulichung relativistischer Raum-Zeit-Verhältnisse auf jeweils zwei Achsen, typischerweise die Achsen x und ict, beschränkt. Für die Abstände zwischen Weltpunkten, die jetzt Raum- und Zeitkoordinaten hatten, galt die alte euklidische Regel quadrierter Koordinaten-Differenzen, allerdings mit einem durch i2 = ─1 veränderten Vorzeichen des zeitlichen Anteils:
ds2 = dx2 + dy2 + dz2 + d(ict)2
Die Lorentztransformationen konnten dann als Drehung in dieser vierdimensionalen Raumzeit verstanden werden, bei der diese Größe ds2 invariant blieb ebenso wie bei Drehung im dreidimensionalen Raum der dreidimensionale Abstand zweier Körper unverändert bleibt. Effekte wie die Lorentzkontraktion und die Zeitdilatation konnten nun als durch Projektion von Längen- und Zeitanteil von eigentlich längen- und zeitbehafteten Größen auf zueinander um den Winkel ß = arctan(v/c) gedrehte Koordinatenachsen anschaulich interpretiert werden.
Mittelpunkt im Universum.
Im Universum ist kein Ort feststellbar, der als Mittelpunkt im Universum bezeichnet werden könnte.
Newtonsche Bewegungsgesetze
Gesetze, welche die Bewegung von Körpern unter Kräfteeinfluss beschreiben, wobei sie voraussetzen, dass Raum und Zeit absolut und unwandelbar sind. Diese Gesetze galten unverändert, bis Einstein die spezielle Relativitätstheorie entdeckt hatte, die zeigt, dass die Newtonsche Theorie nur eine Näherung für den Grenzfall kleinerer Geschwindigkeiten ist.
Photon
Kleinstes Paket des elektromagnetischen Felds. Botenteilchen der elektromagnetischen Kraft. Kleinstes Lichtpaket.
Pseudoeuklidische Geometrie
Während in einem euklidischen Raum das Quadrat des Abstandes zweier verschiedener Punkte P1 und P2 stets größer als Null ist, kann es in der Minkowski-Welt auch kleiner oder gleich Null sein. Die Raumzeit-Union der Relativitätstheorie besitzt also keine euklidische Maßbestimmung. Vielmehr ist die Maßbestimmung die vierdimensionale Verallgemeinerung der pseudo-euklidischen Geometrie. Dies ist der mathematische Ausdruck dafür, dass die Zeitkoordinate eine andere Qualität als die 3 Raumkoordinaten besitzt.
Raum und Zeit als untrennbare Einheit.
Man kann die SRT nicht auf der Grundlage der klassischen Betrachtung mit Trennung von Raum und Zeit verstehen. Man kann die SRT erst dann verstehen, wenn man Raum und Zeit als untrennbare Einheit ansieht.
Raumzeit
Die drei physikalischen Dimensionen des Raums werden mit der Zeit, die als vierte Dimension aufgefasst wird, verknüpft und ergeben so das Raum-Zeit-Kontinuum, das den grundlegenden Rahmen in der Relativitätstheorie darstellt.
Relativgeschwindigkeit.
Jede Geschwindigkeit (eines Körpers oder eines Inertialsystems) ist immer nur eine Relativgeschwindigkeit.
Relativität der Bewegung
Relativ bedeutet, dass die Bewegung nur in Bezug auf ein anderes Objekt festgestellt werden kann. Die Relativität der Bewegung gleichförmig bewegter Objekte ist keine Entdeckung der SRT, sondern wurde bereits von Galileo erkannt.
Relativität der Gleichzeitigkeit.
Das ist die erste Konsequenz der Konstanz der Lichtgeschwindigkeit. Einstein argumentierte etwa wie folgt: Auch die Zeit ist relativ. Es gibt keine absolute Zeit, die für alle Inertialsysteme gültig ist. In jedem Inertialsystem läuft die Zeit anders ab, abhängig davon, wie schnell sich die Inertialsysteme relativ zueinander bewegen. Und das ist ein totaler Umsturz unseres Weltbildes, weil seit Newton die Zeit "überall gleich verfließt". Und genau das tut sie nicht.
Was für einen Beobachter gleichzeitig ist, ist für einen anderen bewegten Beobachter nicht gleichzeitig. Ob zwei räumlich getrennt liegende Ereignisse gleichzeitig sind oder nicht, kann nicht dadurch entschieden werden, dass man mit Hilfe einer Messung die Gleichzeitigkeit zweier Ereignisse feststellen könnte. Der Gleichzeitigkeits-Begriff getrennt liegender Ereignisse erlangt erst durch eine Definition seine Bestimmtheit. Gleichzeitigkeit ist objektiv unbestimmt.
Relativitätsprinzip
Zentraler Begriff der Relativitätstheorie, nach der die physikalischen Gesetze für alle Beobachter, die mit konstanter Geschwindigkeit relativ zueinander bewegt sind, die gleiche Form haben; daher ist jeder dieser Beobachter gleichermaßen zu der Behauptung berechtigt, er befinde sich in Ruhe. Dieses Prinzip wird in der allgemeinen Relativitätstheorie zum Äquivalenzprinzip erweitert. Bereits in der Newtonschen Mechanik waren alle Inertialsysteme gleichberechtigt. Die Newtonschen Axiome der Mechanik zeichnen kein Inertialsystem gegenüber dem anderen aus. Der Übergang von einem Inertialsystem in ein anderes Inertialsystem wird in der Newtonschen Mechanik durch eine Galilei-Transformation vollzogen.
Relativistischer Dopplereffekt
Der relativistische Dopplereffekt hängt nur von der Relativgeschwindigkeit von Sender und Empfänger ab.
Ruheenergie
ist die aus der Beziehung E0 = mc2 berechnete Energie , wobei m die Masse des Teilchens und c die Lichtgeschwindigkeit ist. Die Ruhenergie wird nur dann vollständig freigesetzt, wenn ein Teilchen mit seinem Antiteilchen zerstrahlt.
Ruhesystem.
Man kann sich als Beobachter in jedes beliebige Inertialsystem gedanklich hineinsetzen kann, um dieses Inertialsystem dann zum Ruhesystem zu erklären.
Spezielle Relativitätstheorie
Einsteins Gesetze von Raum und Zeit in Abwesenheit von Gravitation.
SRT als Sonderfall der ART
Die SRT lässt sich als Sonderfall der ART interpretieren, sie ist gültig für einen massefreien Raum. Bei einem masseerfüllten Raum lässt sich die SRT lokal näherungsweise anwenden.
Teilchenbeschleuniger
Anlage, die Teilchen fast auf Lichtgeschwindigkeit beschleunigt und sie dann mit anderen Teilchen zusammenstoßen lässt, um ihren materiellen Aufbau zu ermitteln.
Vektorraum
In der Mathematik eine Gesamtheit von Vektoren, d.h. Objekten, die sich addieren und mit Zahlen multiplizieren lassen. Vektorräume unterscheiden sich nach der Art dieser Zahlen (z. b. reelle oder komplexe Zahlen) und nach ihrer Dimensionszahl. Zum Beispiel bilden die möglichen Geschwindigkeiten im Raum einen dreidimensionalen reellen Vektorraum.
Vierdimensionaler Abstand zwischen zwei Ereignissen.
Für alle inertialen Beobachter ist der vierdimensionale Abstand zwischen zwei Ereignissen in der Raumzeit verbindlich. Alle messen den gleichen Wert. Man sagt, dieser Abstand ist das "Raumzeit-Intervall" und dieses ist invariant für alle Beobachter. Wenn man die zwei Raumdimensionen y und z weglässt und nur eine Raumdimension x und die Zeitdimension t betrachtet, dann ergibt sich das Raumzeit-Intervall s² zwischen zwei Ereignissen für zwei verschiedene Systeme wie folgt:
Wellenlänge
Elektromagnetische Strahlung wird durch ihre Wellenlänge oder ihre Frequenz charakterisiert, deren Produkt gleich der Lichtgeschwindigkeit ist. Die Wellenlänge ist die Entfernung zwischen aufeinanderfolgenden Wellenfronten, und die Frequenz ist die Zahl der Wellenfronten, die an einen gegebenen Punkt in einer Sekunde vorbeilaufen. Im sichtbaren Bereich hat das Licht eine Wellenlänge von 400 bis 700 Nanometer und eine Frequenz von 7 x 1014 bis 4 X 1014 Hertz.
Weltlinie
Eine Abfolge von Weltpunkten.
Weltpunkt
Ein Ort in der Raumzeit. Er ist bestimmt durch vier Koordinaten: {x, y, z, t}
Zwillingsparadoxon.
Gegen Einsteins Zwillingsexperiment wird meist mit der Symmetrie der Zeitdilatation argumentiert:
Wenn Zwilling B einerseits die Uhr von Zwilling A langsamer gehen sieht, dann muss umgekehrt doch Zwilling A auch die Uhr von B langsamer gehen sehen. Das ist zwar richtig, gilt aber nur, solange sich Zwilling A und B jeweils in einem Inertialsystem bewegen. Doch Zwilling B muss umkehren, um zu A zurückkehren zu können, d. h., er beschleunigt und befindet sich daher nicht in einem Inertialsystem, im Gegensatz zu B.
Diese Antwort wiederum hat dazu geführt, dass oftmals die Beschleunigungsphasen von B für die Verjüngung verantwortlich gemacht werden. Aber auch das ist nicht richtig, wie sich leicht zeigen lässt, indem man aus dem Zwillingsparadoxon ein Drillingsparadoxon macht. In der nachstehenden Skizze sind die Weltlinien der Drillinge A, B und C dargestellt, wobei C identische Beschleunigungsphasen (gekrümmte Kurvenstücke, durchgezogen gezeichnet) durchläuft, allerdings ist seine Reise kürzer.

Nach Zusammenkunft aller drei ist A älter als C und C älter als B. Die Beschleunigungsphasen können also nicht für den Altersunterschied verantwortlich gemacht werden. Es ist die physikalische Geometrie der relativistischen Raumzeit: Der Weg von B ist kürzer als der von C, und dieser wiederum ist kürzer als der Weg von A.
Zwillingsexperiment als Quintessenz mehrerer Fach-Autoren.
1. Die Symmetrie der Zeitdilatation wird gebrochen, sobald der reisende Zwilling umkehrt.
2. Die Umkehr ist gleichbedeutend mit einem Inertialsystemwechsel.
3. Der Inertialsystemwechsel bei der Umkehr lässt die auf seiner Reise erarbeitete Zeitdilatation des reisenden Zwillings manifest werden.
4. Die verflossene Eigenzeit, die der jeweilige Zwilling auf seiner Uhr abliest, entspricht der jeweiligen Länge der Weltlinie im Minkowski-Raum.
5. Die Beschleunigungsphasen des reisenden Zwillings sind nicht die Ursache der Zeitdilatation. Man kann die Beschleunigungsphasen durch ein Differenzexperiment zum Verschwinden bringen. Die Zeitdilatation tritt dann trotzdem auf. Die Zeitdilatation ist im wesentlichen abhängig von der Reisedauer und der Reisegeschwindigkeit des reisenden Zwillings.
6. Manche meinen, dass nur die ART das scheinbare Paradoxon auflösen könnte, weil Beschleunigungen im Spiel sind. Mal ganz abgesehen davon, dass man mit der SRT auch Beschleunigungen beschreiben kann, ist die ART zu Auflösung des Zwillingsparadoxons nicht notwendig. Es kann allein mit Mitteln der SRT gelöst werden. Die ART wird nur dann benötigt, wenn die Gravitation ins Spiel kommt.
Herleitung der Lorentz-Transformationen mit Hilfe einer Koordinatensystemdrehung im Minkowski-Raum.
Zunächst wird die gewöhnliche Koordinatentransformation im euklidischen Raum in Skizze 1 dargestellt, so wie sie in jeder Formelsammlung zu finden ist:

Der Mathematiker Hermann Minkowski Minkowski ging von der Invarianz des Linienelementes aus und suchte allgemeine Transformationsgleichungen, die dies gewährleisten. Er hat dabei herausgefunden, dass allgemein jede Transformation zwischen relativ zueinander bewegten Inertialsystemen durch eine Koordinatensystemdrehung um einen imaginären Winkel in einem vierdimensionalen Raum darstellbar ist.
Gegeben sind zwei Inertialsysteme S und S', die sich relativ zueinander mit der Geschwindigkeit v bewegen. Ersetzt man w durch ict und ß durch den imaginären Winkel (iß), dann wird aus der reellen Drehung im euklidischen Raum eine imaginäre Drehung im Minkowski-Raum (x, w=ict). Die imaginäre Einheit in w=ict gewährleistet die pseudoeuklidische Metrik der Minkowski-Raumzeit.
Das ist vorläufig eine willkürliche mathematische Festsetzung ohne physikalische Begründung. Durch diese Festsetzung wird auch der Drehwinkel imaginär. Einstein stand ursprünglich den mathematischen Ideen Minkowskis zur SRT reserviert gegenüber: Er sagte: "Das bringt doch physikalisch nichts Neues!" Später erwies sich Minkowskis imaginärer Ansatz als sehr hilfreich zur späteren mathematischen Herleitung der ART-Gleichungen. Einsteins ursprüngliche Herleitung der ART-Gleichungen war nämlich sehr kompliziert und für einen mathematischen Laien nicht nachvollziehbar. Siehe Skizze 2:

Der Raumzeit-Abstand O-E bleibt durch die Drehung invariant. Das Ereignis E, das im System S durch den Weltpunkt E(x, ict) dargestellt wird, ist im System S’ der Weltpunkt E(x’, ict’). Bei dem Weltpunkt E handelt sich im System S und im System S’ um das gleiche Ereignis, nur die Koordinaten dieses Ereignisses haben im System S andere Werte als im System S’.
Die Transformationsgleichungen nehmen deshalb folgende Gestalt an:
(3) x' = x•cos(iß) + ict•sin(iß); i² = ─ 1
(4) ict' = ict•cos(iß) ─ x•sin(iß)
Zu jedem Zeitpunkt bewegt sich S' mit der Geschwindigkeit v = x/t in Richtung der positiven x-Achse; daraus folgt:
(5) x = v•t
Betrachtet man im 2. Quadranten des Systems S einen beliebigen Punkt (─ x, ict), der auf der auf der Ordinate w=ict' liegt, dann lässt sich für den Winkel (iß) der Tangens bestimmen:
(6) tan(iß) = ─ x/ict; mit x=v•t ergibt sich:
(7) tan(iß) = ─ v•t/ict
Für alle t ungleich Null ergibt sich:
(8) tan(iß) = ─ v/(ic); quadriert ergibt:
(9) tan²(iß) = ─ v²/c²
Der imaginäre Drehwinkel (iß) repräsentiert somit ─ über den Tangens dieses Winkels ─ die Relativgeschwindigkeit zwischen den beiden Inertialsystemen S und S' als Bruchteil der Lichtgeschwindigkeit. Aus einer Formelsammlung entnehme ich die Umformungen (10) und (11):
(10) sin(iß) = tan(iß)/sqrt[1 + tan²(iß)]
(11) cos(iß) = 1/sqrt[1 + tan²(iß)]
Mit der Kurzschreibweise G = 1/sqrt[1 + tan²(iß)] ergibt sich:
(12) sin(iß) = G•tan(iß)
(13) cos(iß) = G; (12) und (13) in (3) eingesetzt ergibt:
(14) x' = x•G + ict•G•tan(iß); mit tan(iß) = ─ v/(ic) ergibt sich:
(15) x' = x•G + ict•G•[─ v/(ic)]
(16) x' = x•G ─ t•G•v
(17) x' = G(x ─ v•t); aus (4) und (12) und (13) ergibt sich:
(18) ict' = ict•G ─ x•G•tan(iß); mit tan(iß) = ─ v/(ic) ergibt sich:
(19) ict' = ict•G ─ x•G•[ ─ v/(ic)]
(20) ict' = G[ ict ─ x•[ ─ v/(ic)] ]
(21) ict' = G[ict + x·v/(ic)]; dividiert durch (ic) ergibt:
(22) t' = G(t ─ x•v/c²)
Wenn man die Beziehung (9) in die Kurzschreibweise
G = 1/sqrt[1 + tan²(iß)] einsetzt, dann ergibt sich:
(23) G = 1/sqrt(1 ─ v²/c²)
Diese Gleichung in (17) und (22) eingesetzt ergeben die speziellen Lorentz-Transformationen:
x' = (x ─ v•t) / sqrt(1 ─ v²/c²)
t' = (t ─ v•x/c²) / sqrt(1 ─ v²/c²)
13.12.2014 Lorentz-Kontraktion neu eingetragen.
Beitrag zuletzt bearbeitet von Bauhof am 13.12.2014 um 11:45 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 1.375, Mitglied seit 16 Jahren |
Beitrag Nr. 1991-4
13.12.2014 11:46
|
:idea: :idea:
:idea: :idea:
:idea:
 :idea:
:idea: :idea:
:idea:
[Gäste dürfen nur lesen]
In diesem Forum dürfen nur Mitglieder schreiben. Hier kannst du dich anmelden


 Nach oben
Nach oben