|
Otto
Beiträge: 1.246, Mitglied seit 10 Jahren
|
Beitrag Nr. 2363-1
07.06.2021 08:09
|
In der klassischen Physik ist die aktuelle Distanz eine räumliche Entfernung zwischen zwei Punkten, die konstant oder zeitlich veränderlich ist und die nach einem definierten Normalmaß, einem Talon, bemessen wird.
Für die Zeitdauer ist die s.g. Atomuhr als Normalmaß vereinbart. Die Maßeinheit der Zeit ist als Vielfaches einer Periode einer elektromagnetischen Wellenresonanz des Cäsium-Atoms definiert. Die Periode ist die Zahl der Wellenzüge des Überganges eines Elektrons von einem Energiezustand auf einen anderen.
Längendilationen, Raumkrümmung und Zeitdilationen sind aus der ART und SRT bekannt.
Die räumliche Volumendilatation (dx = dy = dz) ist durch die Rotverschiebung nachweisbar.
Roger Penrose schlug vor, die räumliche Expansion des Alls mittels veränderlichen Maßstabes mathematisch zu beschreiben. Er nennt dies "mitbewegte Entfernung" (commoving distance) und versteht darunter einen Maßstab, der mit dem Universum wächst. Es ist ein Maßstab, dessen Abstände sich zwischen den Markierungen dehnen, die Zahlen der Abstandsmarken sich jedoch nicht ändern (wie auf ein Gummi-Lineal). Die "mitbewegte Entfernung" ist eine dimensionslose prozentuale Größe, die sich mit der Zeitdauer ändert. (1)
Weiterhin unterscheidet Roger Penrose (Nobelpreisträger 2020) zwischen der üblichen normalen Zeit (time) und der s.g. "konformen Zeit" (conformal time), eine veränderliche Zeit, deren Maßstab sich in gleicher Weise ändert wie die mitbewegte Entfernung (dx = dy = dz =dt). In einem Koordinatensystem mit der mitbewegten Entfernung auf der X-Achse und der konformen Zeit auf der Y-Achse, wird dann die Weltlinie eines Lichtstrahls zu einer Geraden Y = X (das heißt eines um 45° "winkeltreu" geneigten Strahls).
Im Folgenden wird analysiert, ob sich diese Gendanken von Roger Penrose, den er für das expandierende Universum applizierte, ganz allgemein auf Geschwindigkeiten anwenden lässt.
Die Idee der mitbewegten Entfernung von Penrose wird auf die "Laufzeit-Entfernung" angewendet und analysiert.
Gruß, Otto
(1) Die Länge einer Strecke nimmt im Vakuum gegenwärtig um 0,00000000757% pro Jahr zu.
Für die Zeitdauer ist die s.g. Atomuhr als Normalmaß vereinbart. Die Maßeinheit der Zeit ist als Vielfaches einer Periode einer elektromagnetischen Wellenresonanz des Cäsium-Atoms definiert. Die Periode ist die Zahl der Wellenzüge des Überganges eines Elektrons von einem Energiezustand auf einen anderen.
Längendilationen, Raumkrümmung und Zeitdilationen sind aus der ART und SRT bekannt.
Die räumliche Volumendilatation (dx = dy = dz) ist durch die Rotverschiebung nachweisbar.
Roger Penrose schlug vor, die räumliche Expansion des Alls mittels veränderlichen Maßstabes mathematisch zu beschreiben. Er nennt dies "mitbewegte Entfernung" (commoving distance) und versteht darunter einen Maßstab, der mit dem Universum wächst. Es ist ein Maßstab, dessen Abstände sich zwischen den Markierungen dehnen, die Zahlen der Abstandsmarken sich jedoch nicht ändern (wie auf ein Gummi-Lineal). Die "mitbewegte Entfernung" ist eine dimensionslose prozentuale Größe, die sich mit der Zeitdauer ändert. (1)
Weiterhin unterscheidet Roger Penrose (Nobelpreisträger 2020) zwischen der üblichen normalen Zeit (time) und der s.g. "konformen Zeit" (conformal time), eine veränderliche Zeit, deren Maßstab sich in gleicher Weise ändert wie die mitbewegte Entfernung (dx = dy = dz =dt). In einem Koordinatensystem mit der mitbewegten Entfernung auf der X-Achse und der konformen Zeit auf der Y-Achse, wird dann die Weltlinie eines Lichtstrahls zu einer Geraden Y = X (das heißt eines um 45° "winkeltreu" geneigten Strahls).
Im Folgenden wird analysiert, ob sich diese Gendanken von Roger Penrose, den er für das expandierende Universum applizierte, ganz allgemein auf Geschwindigkeiten anwenden lässt.
Die Idee der mitbewegten Entfernung von Penrose wird auf die "Laufzeit-Entfernung" angewendet und analysiert.
Gruß, Otto
(1) Die Länge einer Strecke nimmt im Vakuum gegenwärtig um 0,00000000757% pro Jahr zu.
Beitrag zuletzt bearbeitet von Otto am 07.06.2021 um 08:34 Uhr.
[Gäste dürfen nur lesen]
|
Otto
Beiträge: 1.246, Mitglied seit 10 Jahren
|
Beitrag Nr. 2363-2
07.06.2021 08:23
|
Otto schrieb in Beitrag Nr. 2363-1:Die Idee der mitbewegten Entfernung von Penrose wird auf die "Laufzeit-Entfernung" angewendet und analysiert.
Zusammenfassung - Maßstabsänderung von Raum und Zeit für die Laufzeitentfernung
Die Ergebnisse sind überraschend.
1. Der Zeitfluss ist nicht konstant, sondern eine veränderliche Größe. Über die Zeitdauer verändert sich der Zeitablauf.
Der Maßstab der Zeit folgt dem Logarithmus naturalis.
Die Zeit verläuft kurz nach einem Ereignis anfangs schneller, später langsamer.
2. Die Definition eines Einheitswertes 1 als Maßzahl für die Zeit und der Maßzahl 1 für die räumliche Entfernung lässt sich rein mathematisch begründen (völlig unabhängig von den willkürlich festgelegten Maßstäben wie Urmeter und Atomuhr).
3. Die Raumzeit ist bei jeder Relativbewegung gekrümmt, verursacht durch Energie und Impuls der physikalischen Krümmung.
Merkmal von Licht ist, dass die Krümmungen von Zeit und von räumlicher Dimension gleich sind.
4. Die Krümmungen, als Maß der Änderung, von Zeitdauer und der Distanz gehen mit zunehmender Zeit gegen Null (konstanter Zeitfluss).
Zeitdauer und räumliche Entfernung wachsen gegen Unendlich. Dies gilt allerdings nur für eine 1-dimensionale räumliche Beziehung zwischen Beobachter und Objekt. Für den dreidimensionalen Raum streben Zeit/Entfernung gegen einen endlichen Grenzwert (π).
5. Die Veränderung des Maßstabes, d.h. die Änderung der Skalierung, ist im Grunde nur eine Koordinatentransformation.
Der γ-Faktor der SRT lässt sich als Verhältnis verschiedener Maßstäbe beschreiben.
Es ist γ² = 1/[1 – (Yc/Yv)²] mit den unterschiedlichen Zeitmaßstäben Y für Licht und für eine Relativgeschwindigkeit v bzw. γ² = 1/[1 – (Xv/Xc)²] mit den unterschiedlichen Zeitmaßstäben X der räumlichen Dimension.
6. Die Änderung des Entfernungsmaßstabes und die Änderung des Zeitmaßstabes sind durch eine Hyperbelgleichung miteinander verknüpft.
Der Wert des Krümmungsradius im Scheitelpunkt der Hyperbel ist identisch mit dem Radius bis zum Scheitelpunkt - wie vom Schwarzschildradius her bekannt - hier durch das Energieniveau der physikalischen Wirkung verursacht. Die Krümmung der Zeit, (als Maß der Steigungsänderung der Hyperbel) tritt auch beim Aussenden von masselosen Photonen auf.
Dieser Kreisradius beschreibt in diesem Falle keine Grenze für Information und kausale Zusammenhänge, sondern ist der Spiegel von Zeitdauer und Distanz.
Die Spiegelung erfolgt am Kreisumfang, die das Äußere des Kreises auf das Innere des Kreises abbildet. So werden Zeit und Raum zueinander Spiegelungen ein und desselben.
Zeit und Raum sind zueinander austauschbar.
Die Kreislinie markiert den Ist-Zustand, den Augenblick.
Den Raum erleben wir. Er ist unsere Erlebniswelt.
Zeit erleben wir nicht; Zeit können wir mit keinem unserer Sinnesorgane wahrnehmen. Die Daten einer Zustandsänderung, der Zeit, existiert nur als gespeicherte Information in unserem Gedächtnis.
Signale sind das Ergebnis der Zeit-Veränderung.
7. Die mathematisch-geometrische Spiegelung von Raum und Zeit am Kreis lässt sich auch prosaisch formulieren:
Der Raum ist der "Schatten" der Zeit. Dieser Schatten ist unsere Erlebniswelt.
Diese Interpretation beantwortet die Frage nach einer (möglichen) Ursache von Raum bzw. einer räumlichen Dimension.
Einstein hat in Bezug auf die Raumzeit formuliert: "Zeit und Raum sind nur Methoden, anhand deren wir denken, und keine Bedingung, in der wir leben."
8. Wenn die Zeit Ausdruck einer Zustandsänderung ist, dann gibt es ohne Zustandsänderung keine Zeit.
Die Relativgeschwindigkeit ist eine Zustandsänderung. So, wie sich eine Entfernung ändert, ändert sich bei einer konstanten Geschwindigkeit im gleichen Maße auch die Zeitdauer. Das gilt für jede Relativgeschwindigkeit, einschließlich der Lichtgeschwindigkeit.
Merkmal der Lichtgeschwindigkeit sind identische Maßstäbe für Raum und für Zeit.
Eine Relativgeschwindigkeit v unterscheidet sich von der Lichtgeschwindigkeit c nur durch unterschiedliche Maßstäbe für Raum und für Zeit.
Die Lichtgeschwindigkeit lässt sich als "Normalzustand" unserer Welt verstehen.
Die Relativbewegung ist nur eine Abweichung von diesem Normalzustand.
Roger Penrose ist der Auffassung, dass die Lichtgeschwindigkeit deshalb ihren Sinn als Naturkonstante verliert.
9. Die Zustandsänderung der Distanz bzw. des Raumes ist Ausdruck von Zeit und gleichbedeutend mit der Zeit.
Folglich kann infolge der Symmetrie von Zeitdauer und Distanz die Relativgeschwindigkeit zwischen zwei Objekten als die Wirkung unterschiedlicher Eigenzeiten zweier Punkte (2) interpretiert werden.
Der Zeitmaßstab definiert die Eigenzeiten.
Das Resultat sind unterschiedliche Zeitdauern für einen Beobachter und einem dazu relativ bewegten Objekt.
Für das bewegte Objekt ändert sich also eigentlich nicht die Entfernung.
Wir erleben es nur so und definieren die Differenz der unterschiedlichen Eigenzeiten als Relativgeschwindigkeit.
Wir erleben nur die Zeit, interpretieren sie aber als Raum.
10. Zeitdauer und Distanz als Integral dieser Änderungen lassen sich zweckmäßig in einem doppelt-logarithmischen Koordinatensystem darstellen. Zur graphischen Darstellung von Zeitdauer und Distanz bietet sich ein ln-ln-Plot mit einer Teilung n auf Basis en und der Eulerzahl e = 2.72… als Basis an.
Durch diese Darstellung wird eine Hyperbel im logarithmischen Koordinatensystem zu einer Geraden (3) Die Gerade gilt für jede beliebige Relativgeschwindigkeit, nicht nur für die Lichtgeschwindigkeit.
Für den speziellen Fall der Lichtgeschwindigkeit wird diese Gerade zum bekannten Lichthorizont bzw. Ereignishorizont.
11. Der veränderliche Maßstab der Zeit ist durch unsere logarithmische Erlebniswelt verdeckt.
Unsere Welt ist eigentlich eine logarithmische Welt.
Erst die geometrische Darstellung mittels eines ln-ln-Plots führt zu den bekannten linearen Zusammenhängen von Raum und Zeit (für konstante Relativgeschwindigkeiten), wie wir sie erleben und messen.
12. Der Urknall ist ursächlich eine spontane Änderung der Zeit, die wir als Quelle von Photonen erleben.
Die Rotverschiebung ist Ausdruck der Änderung der Zeit seit dem Urknall. Wir messen die heutige Frequenzverschiebung des Photonen-Impulses und interpretieren sie als Expansion des Raumes.
Die Rotverschiebung wird nicht durch die Expansion des Raumes verursacht, sondern durch die "Alterung" der Zeit.
Gruß, Otto
(2) Die Relation eines Punktepaares lässt sich als Eigenschaft eines einzelnen Punktes interpretieren. Denn jedes einzelne Ding kann nach der Mengenlehre zu sich selbst in Relation stehen, als s.g. reflexive Beziehung. Die Relation des Punktepaares ist der Einzelpunkt selbst.
Die Relation ist das Verhältnis der beiden Maßstäbe der Zeit und der Raumdimension.
Das ganze Universum bestünde dann nur aus sich ständig verändernden Relationen eines einzigen Punktes.
Siehe https://de.wikipedia.org/wiki/Relation_(Mathematik) und Beitrag Nr. 2358-24 und Beitrag Nr. 2358-36.
(3) Die Gerade ist ein geometrisches Objekt ohne innere Eigenschaften. Von Bedeutung sind nur die Beziehungen zwischen Punkten.
Die kürzeste Verbindung zwischen zwei Punkten ist eine Strecke (Distanz, Entfernung).
Am 7-SEP-2021 redaktionell überarbeitet und ergänzt.
Beitrag zuletzt bearbeitet von Otto am 07.09.2021 um 05:51 Uhr.
[Gäste dürfen nur lesen]
|
Otto
Beiträge: 1.246, Mitglied seit 10 Jahren
|
Beitrag Nr. 2363-3
07.06.2021 16:10
|
Otto schrieb in Beitrag Nr. 2363-2:1. Der Zeitfluss ist nicht konstant, sondern eine veränderliche Größe. Über die Zeitdauer verändert sich der Zeitablauf.
Änderung des Zeit-Maßstabes und Änderung des Weg-Maßstabes
In der klassischen Physik ist der Betrag der durchschnittlichen Geschwindigkeit das Verhältnis von Distanz zu Zeitdauer. Die Momentangeschwindigkeit ist der Grenzwert dieses Verhältnisses, wenn das Zeitintervall gegen Null strebt.
Diese Auffassung geht von einem kontinuierlichen Zeitfluss aus, dessen Maßstab stets konstant ist.
Die folgenden Ausführungen gehen von dem Gedankenspiel aus, dass sich nicht nur der Weg, sondern auch die Zeit ändern kann.
Das Maß der Zustandsänderung (vs) des Weges s ist zu einem Zeitpunkt t0.
ds meint die differentielle Änderung der Distanz.
Das Maß der Zustandsänderung (vt) der Zeit t ist an einem Ort s0
Beide Zustandsänderungen, die des Weges und die der Zeit, sind dann identisch, wenn vs = vt ist.
Daraus ergibt sich die Gleichung einer Hyperbel mit den Variablen ds und dt.
dt ist die differentielle Änderung des Zeitvergehens.
Beide Zustandsänderungen, die des Weges und die der Zeit, sind dann identisch, wenn vs = vt ist.
Daraus ergibt sich die Gleichung einer Hyperbel mit den Variablen ds und dt.
S0 ist die sogenannte "physikalische Wirkung" in [J∙s].
F0 ist die Wirkung eines Potentials als Kraft [N].
Geometrisch stellte das Produkt ds∙dt eine Hyperbel mit den Variablen ds und dt dar. Der Krümmungsradius rs im Scheitelpunkt der Hyperbel hat den Wert rs² = 2(s0∙t0) = 2S0/F0.
Physikalisch lässt sich die Beziehung "Wegänderung mal Zeitänderung" mit der Einheit [m∙s] als Wirkung [J∙s] pro Krafteinheit F0 = 1 [N] interpretieren.
- Die Kraft F0 bedeutet hier den Effekt eines Potentials. (Die Krafteinheit von 1 [N] ist als s.g. Gewichtskraft definiert, die auf einen Körper mit einer Masse m = 102 g auf der Erde in Meereshöhe wirkt.)
- Die physikalische Wirkung S0 ist das Produkt aus Energie und Zeit mit der Einheit [J∙s]. Die Wirkung ist das Merkmal von Bewegungsgleichungen, die dem Prinzip der kleinsten Wirkung folgen (Hamiltonsches Prinzip).
Die Beziehung (ds∙dt) bedeutet demzufolge physikalisch, dass der Weg zwischen zwei festen Punkten so erfolgt, dass dafür ein Minimum an Energie erforderlich ist, und dass sich diese Bewegung in einem Potentialfeld vollzieht.
Diese energetische Optimierung der Bewegung im Raum (Maßeinheit [m]) erfolgt durch die Änderung der Geschwindigkeitsrichtung des Körpers oder durch die Änderung des Geschwindigkeitsbetrages (des Impulsvektors m∙v).Die Beziehung (ds∙dt) bedeutet demzufolge physikalisch, dass der Weg zwischen zwei festen Punkten so erfolgt, dass dafür ein Minimum an Energie erforderlich ist, und dass sich diese Bewegung in einem Potentialfeld vollzieht.
Diese energetische Optimierung der Bewegung im Raum (Maßeinheit [m]) erfolgt durch die Änderung der Geschwindigkeitsrichtung des Körpers oder durch die Änderung des Geschwindigkeitsbetrages (des Impulsvektors m∙v).
In der geometrischen Darstellung repräsentiert der Radius des Krümmungskreises im Scheitelpunkt der Hyperbel die Energie [J] eines Körpers, der sich in einem Gravitationsfeld bewegt.
Der Krümmungsradius rs im Scheitelpunkt der Hyperbel beträgt rs² = 2S0/F0.
Der Abstand des Scheitelpunktes vom Koordinatenursprung ist identisch mit dem Krümmungsradius rs im Scheitelpunkt.
So spiegelt der Wert der Wirkung S0 die Lage des Hyperbelscheitelpunktes im Koordinatensystem wider.
Die beschriebenen Beziehungen lassen sich formal durch die Herleitung mittels Gleichungen begründen.
dt ist die benötigte Zeit, um den Impuls p zu verändern und damit die Geschwindigkeit v eines Körpers zu variieren.
p ist der Impulsvektor mit Betrag und Richtung.
F ist der Kraftvektor, der nötig ist, um Betrag und Richtung der Geschwindigkeit eines Körpers zu verändern.
S ist die physikalische Wirkung = (ds∙p) = "Länge mal Impuls"
Unter mathematischen Gesichtspunkten ist die Wirkung eine Operation eines aktiven Teiles einer Menge auf eine andere passive Teilmenge.
Meines Erachtens ist die Zeitdauer der aktive Teil einer Menge und die Entfernung (die räumliche Dimension) der passive Teil einer anderen zweiten Menge.
So wird die (räumliche) Dimension eine Folge der Hintereinanderausführung der Zeit (siehe https://de.wikipedia.org/wiki/Gruppenoperation ).
Beide Mengen, Zeit und Dimension, existieren nur gleichzeitig, sind bijektiv und komplementär.
Die vorgestellte enge Verbindung zwischen Zeitdauer und Entfernung benötigt keine Annahme der Lokalität, sondern beschreibt die Entfernung unserer Erlebniswelt als Objekte mit verschiedenen Eigenzeiten.
Zeit und Dimension stellen einen gemeinsamen Zustand dar, der durch Verschränkungen von Elektronen / Photonen bekannt ist.
Zur Erinnerung: Zeit und Dimension sind Gradienten von Zeitdauer und Entfernung. Zeitdauer und Entfernung sind Summen (Integrale) von aufeinanderfolgenden Ist-Zuständen.
Wird vereinfachend S0/F0 = 1 gesetzt, dann ist die Änderung des Wegmaßstabes der Änderung des Zeitmaßstabes umgekehrt proportional (Längendilatation = 1/Zeitdilatation).
Auf Wirkungen S0 ungleich 1 wird später weiter unten eingegangen.
Daraus ergibt sich die folgende graphische Darstellung:
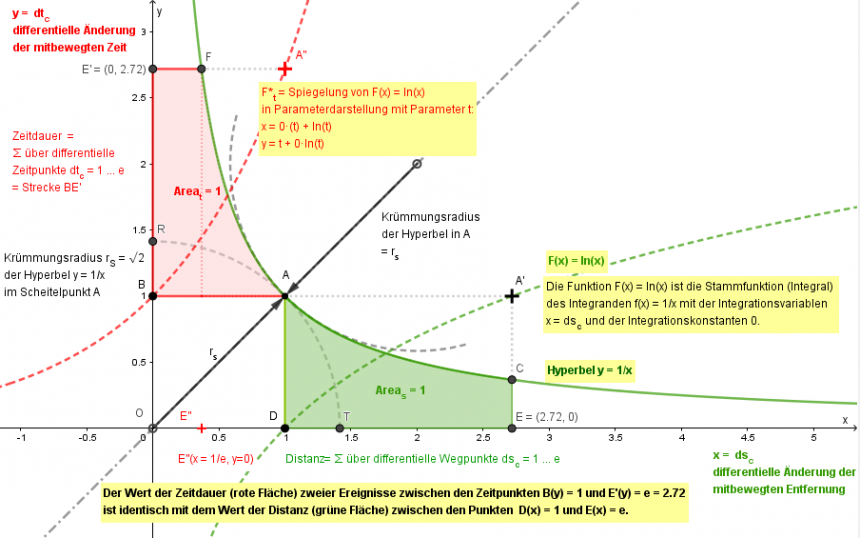
Bild: Relativbewegung als differentielle mitbewegte Entfernung und differentielle mitbewegte (konforme) Zeit in einem dezimalen x-y-Koordinatensystem
Im Diagramm sind auf der Abszisse x die Entfernung-Maßstabsänderung und auf der Ordinate y die Zeit-Maßstabsänderung aufgetragen. Beide Maßstäbe sind durch die Hyperbelgleichung y = 1/x miteinander verknüpft.
Weiter unten in diesen Ausführungen wird gezeigt, dass die Hyperbel den Lichthorizont (Nachkegel) präsentiert. In einem logarithmischen X-Y-Diagramm mit Zeitdauer und Distanz wird die Hyperbel zur Geraden des Lichthorizonts.
Der Krümmungsradius im Scheitelpunkt A der Hyperbel y = 1/x ist identisch mit dem Kreisradius rS um den Koordinatenursprung L(0,0).
Diese Beziehung ist aus der ART als Schwarzschildradius bekannt, wird hier jedoch nicht durch eine Masse verursacht, sondern ganz allgemein von einem Energiepotential. Das Energiepotential ist durch Impuls (m∙v) und ein Schwerefeld in Form einer Kraft F (oder Trägheit einer Masse) bestimmt.
Auf eine physikalische Interpretation dieser geometrischen Zusammenhänge wird später weiter unten noch näher eingegangen.
Diese Stammfunktion F(x) = ln(x) stellt das Integral der Hyperfunktion y = 1/x dar. Für x = e nimmt die Stammfunktion F(x) den Wert 1 an. Anders ausgedrückt, die Fläche unter der Hyperbelkurve hat im Bereich x = 0 … e den Wert 1.
So ist es möglich, einen Einheitswert 1 für die Zeitdauer und für die räumliche Entfernung als rein mathematische Größe in Verbindung mit der Eulerzahl e zu begründen.
Euler hat übrigens genau auf diese Weise die Zahl e hergeleitet, allerdings seinerzeit durch Annäherungen mittels veränderlichen breiten Balkens und deren Höhen y = 1/x.
Es bedarf experimenteller Messungen, um diese mathematischen Einheitswerte mit Werten des internationalen Einheitensystems von physikalischen Größen bzw. Naturkonstanten zu ermitteln.
Die im Diagramm dargestellte Funktion F* stellt die Spiegelung der Funktion F an der Geraden y = x dar. Die Funktion F* = F*(x(t), y(t)), in Parameterdarstellung mit dem Parameter t (t ist hier nicht die Zeit!), lässt sich auch in folgernder Form schreiben:
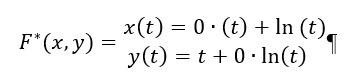
Die Zeitdauer F*, bezogen auf die y-Achse, wächst genauso wie die Entfernung, anfangs schnell und später nur schwach progressiv.
Die Darstellung der ln-Funktion F* mittels eines Parameters t ist interessant.
Sie zeigt den engen Zusammenhang zwischen der ursprünglichen Funktion F = ln(x), überlagert von der linearen Funktion des Parameters t bezogen auf die r y-Achse.
Der "Zeit-Fluss" ist nicht linear, sondern folgt dem Logarithmus naturalis mit der Eulerzahl e = 2,718281828… als Basis.
Das hat keinen Einfluss auf eine gemessene Relativgeschwindigkeit, da sich nicht nur die Zeit, sondern auch die Distanz in gleicher Weise nach einer ln()-Funktion entwickelt.
Für die Geburt unseres Universums, dem Urknall, sind die Verhältnisse etwas anders.
Siehe hierzu die separten Ausführungen in den folgenden Beiträgen.
Die Änderung der Distanz ergibt sich aus der 2. Ableitung der der Stammfunktion F(x) = ln(x), bzw. der 1. Ableitung der Hyperbel y = 1/x.
Die Krümmung F'' beschreibt die Abweichung von einer Geraden. Sie ist negativ, weil die Hyperbel y = 1/x für x > 1 eine fallende Kurve ist.
Der Betrag der Änderung der Funktion F(x) ist für x = 1 am größten.
Für große Distanzen (und Zeitdauern) wird die progressive Änderung immer kleiner und nähert sich einem nahezu konstanten "Zeitfluss" immer mehr an.
Interessant wäre eine analoge Analyse von Zustandsänderungen, die sich nicht unmittelbar auf einen Weg beziehen. Dazu gehören zum Beispiel radioaktive Zerfallsprozesse bzw. die Masse-Energie-Äquivalenz (mit und ohne Abgabe von Masse) eines quantenphysikalischen Zerfallkanals.
Solche Prozesse ließen sich durch die Änderung des Krümmungsradius des Hyperbelscheitelpunktes beschreiben.
Wachstumsprozesse folgen in der Natur jedoch ohnehin einer e-Funktion, deren Zustandsänderung vom aktuellen Ist-Wert bestimmt wird.
Die im Bild an der Geraden y = x dargestellte Spiegelung von Zeitdauer und Distanz im x-y-Diagramm bedarf einer genaueren Verifizierung:
Die Fläche eines Rechtecks mit der Kantenlänge x und y zum Punkt (x,y) auf der Kurve ist stets konstant und hat die Fläche x∙y = a². Die Funktion y = a²/x stellt eine Hyperbel (4) mit dem Scheitelpunkt A(a,a) = A(1,1) dar. Der Krümmungsradius rs im Scheitelpunkt der Hyperbel ist rs² = a² + a² = 2a²..
Im folgenden Bild wird der spezielle Fall a = 1 und x = e graphisch dargestellt.
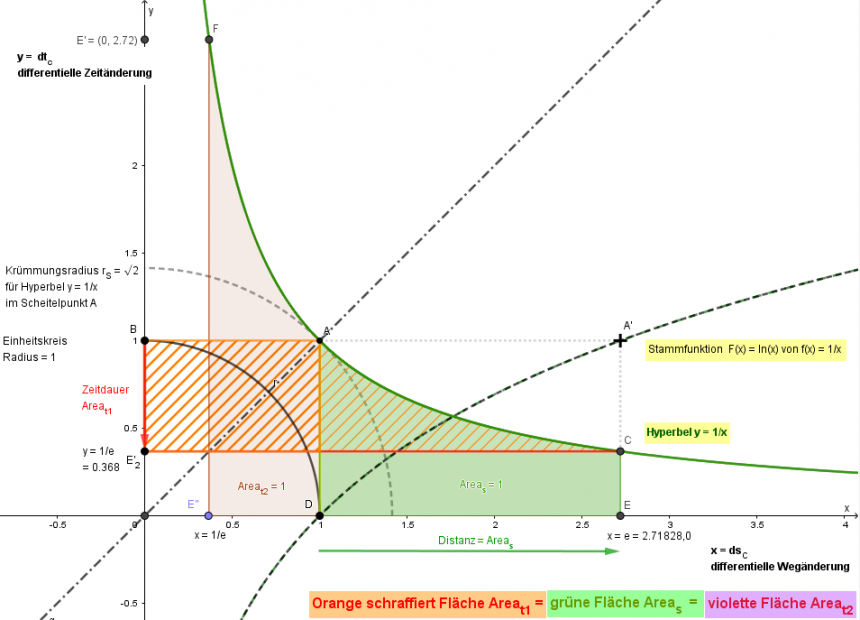
Bild: Äquivalenz der Flächen für Zeitdauer und Distanz
Der Punkt C auf der Hyperbelkurve y = 1/x hat die Koordinaten (x,y) = (e,1/e).
Der Augenblick E'2 und der aktuelle Ort E sind geometrisch über den Kehrwert verknüpft.
Die orangefarben schraffierte Fläche stellt die Zeitdauer dar, die grüne Fläche die Distanz.
Mit fortschreitender Zeit werden auf der Hyperbel, beginnend mit Punkt A (x = 1) und endend mit Punkt C (x = e), gleichzeitig zwei Flächen aufgespannt, die grüne Fläche und die orange schraffierte Fläche. Die grüne Fläche Areas und die orange schraffierte Fläche Areat1 haben den gleichen Zahlenwert.
Auch die violette Fläche Areat2 hat den gleichen Wert wie die grüne Fläche Areas.
Das lässt sich durch die folgenden Gleichungen begründen.
Die Distanz ist für einen (beliebigen) Parameterwert t
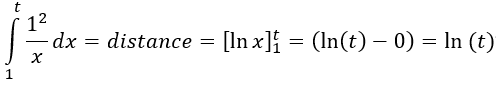
Die Zeitdauer ist
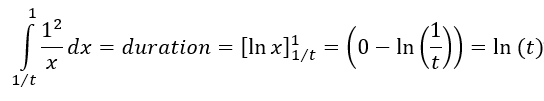
Die Integrale verdeutlichen, dass Zeitdauer und Distanz in der geometrischen Darstellung einen gemeinsamen Ursprung im Scheitelpunkt der Hyperbel haben, markiert durch die Integrationsgrenze mit dem Wert 1.
Der Scheitelpunkt A ist eine Art gemeinsamer "Quelle" von Zeit und Raum.
Die Integrationsgrenze 1 ist bei beiden Integralen einmal als untere, im anderen Fall als obere Integrationsgrenze eingesetzt. So wird erreicht, dass beide Werte positiv bleiben.
Die zweite Integrationsgrenze ist der Parameter t bzw. der Kehrwert 1/t.
Die Integrationsgrenzen t und 1/t sind Spiegelungen am Einheitskreis.
Damit wird das Integral (bildlich dargestellt als Fläche) zwischen 1 und einem beliebigen Punkt t >1 außerhalb des Kreises zu einer Spiegelung des Integrals zwischen 1 und einem Punkt 1/t <1 im Inneren des Kreises.
Die beiden Gleichungen führen zum gleichen Ergebnis ln(x).
Die Flächen für Zeitdauer und Distanz ergeben den gleichen Wert, wenn die Integrationsgrenzen Spiegelwerte sind.
So werden Zeitdauer (duration) und Distanz (distance) zueinander spezielle konforme Transformation mittels reziproker Radien.
Raum und Zeit sind mathematisch nur Spiegelbilder zueinander.
Raum und Zeit existieren nur zusammen als ein mathematisches Objekt. (5)
Deshalb lässt sich aus den geometrischen Darstellungen nicht die Frage beantworten, ob während des s.g. Urknalls nur die Zeit oder nur der Raum existierte.
Was wir mit unseren Sinnen erleben ist nur der Raum.
Zeit erleben wir nicht mit unseren Sinnen. Zeit als geschichtliche Ereignisse registrieren wir nur Dank unseres Gedächtnisses.
Die mathematisch-geometrische Spiegelung von Raum und Zeit am Kreis lässt sich auch etwas prosaisch formulieren:
Der Raum ist der "Schatten" der Zeit. Dieser Schatten ist unsere Erlebniswelt.
Diese Interpretation beantwortet die Frage nach einer (möglichen) Ursache von Raum bzw. einer räumlichen Dimension.
Die Änderung der Zeit ist umgekehrt proportional zur Änderung der räumlichen Distanz, dt ∼ 1/ds.
Ist die differentielle Änderung der Zeit dt sehr groß, dann ist die differentielle Änderung der räumlichen Dimension ds sehr klein. Kurz nach dem Urknall verläuft deshalb die Zeit sehr schnell bei geringer Expansion.
Ist die differentielle Änderung der Zeit dt sehr klein, dann ist die differentielle Änderung der räumlichen Dimension ds sehr groß. Gegen Ende der Existenz des Universums expandiert es räumlich immer schneller, wobei die Zeit immer langsamer verläuft.
Groß, Otto
(4) Die Gleichung der Hyperbel y = a²/x mit a = 1, wie im x-y-Diagramm dargestellt, lässt sich auch allgemeiner als Gleichung x² - y² = a² = 1 (in einem um 45° gedrehten Koordinatensystem) umstellen.
Genau diese mathematische Form entspricht der Ausgangsgleichung der ART von Einstein.
(5) Eine Analogie ist bei Wellenfunktionen zu finden; Wellenfunktionen haben sowohl Eigenschaften von Teilchen als auch von Wellen gleichzeitig. Licht ist weder Welle noch Teilchen allein.
Anmerkungen: Am 15-JUN-2021 das Hamiltonsche Prinzip (Wirkung) eingeführt und die Gleichung ds∙dt = s0∙t0 entsprechend korrigiert.
Am 21-JUN-2021 die Gleichungen zur Herleitung der physikalischen Wirkung S ergänzt.
Am 7-SEP-2021 redaktionell überarbeitet und ergänzt.
Beitrag zuletzt bearbeitet von Otto am 07.09.2021 um 05:50 Uhr.
[Gäste dürfen nur lesen]
|
Otto
Beiträge: 1.246, Mitglied seit 10 Jahren
|
Beitrag Nr. 2363-4
08.06.2021 00:25
|
Otto schrieb in Beitrag Nr. 2363-2:4. Die Krümmungen der Zeitdauer und der Distanz gehen mit zunehmender Zeit/Entfernung gegen Null (konstanter Zeitfluss).
Zeitdauer und räumliche Entfernung wachsen gegen Unendlich. Dies gilt allerdings nur für eine 1-dimensionale räumliche Beziehung zwischen Beobachter und Objekt. Für den dreidimensionalen Raum streben Zeit/Entfernung gegen einen endlichen Grenzwert (π).
Unendliche Entfernung und unendliche Zeitdauer
Im Folgenden werden die Grenzwerte für verschiedene Fälle analysiert, wenn die Werte gegen Unendlich gehen.
(a) Entfernung und die Zeitdauer →∞
Die Fläche unter der Hyperbelkurve 1/x ist.
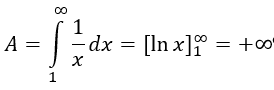
Sowohl die Entfernung als auch die Zeitdauer werden jeweils im Integrationsbereich x = 1…∞ bzw. y = 1…∞ unendlich groß.
(b) Differentielle Zeitänderung→∞
Die differentielle Zeitänderung y = dtc geht mit wachsender differentieller Wegänderung x = dsc gegen Null.
(c) Differentielle Wegänderung →∞
Ebenso geht die differentielle Wegänderung x = dsc mit wachsender differentieller Zeitänderung y = dtc gegen Null.
(d) Endliches Volumen eines Rotationskörpers mit einer unendlichen Oberfläche für eine Rotation um die x-Achse und x →∞
Analysiert wird der Rotationskörper, der durch eine rotierende Fläche zwischen der Hyperbel y = 1/x und x-Achse gebildet wird und um die x-Achse rotiert.
Der Rotationskörper erstreckt sich über eine Länge von x = 1 bis x = ∞.
Der Umfang dieses Rotationskörpers an einer Stelle x ist y(x) = 2π∙1/x.
Dann ist die Oberfläche O des Rotationskörpers
Die Querschnittsfläche des rotierenden Körpers an der Stelle x ist eine Kreisfläche y(x) = π∙(1/x)².
Dann ist das Volumen V des Rotationskörpers
Der Vergleich der beiden Werte zeigt, dass das Volumen des Rotationskörpers den endlichen Wert π hat, während die Oberfläche unendlich groß ist.
In diesem Zusammenhang einen Hinweis: Das Integral über die Krümmung F''(x) = f'(x) = -1/x² im Integrationsbereich x = 1…∞ ergibt den endlichen Wert V*=-1.
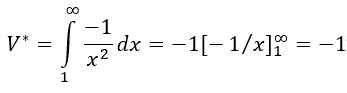
V* ist negativ, weil die Kurve f(x) = 1/x mit zunehmendem x fällt.
Während das Integral der Kurve 1/x² (für den Bereich x = 1…∞) den endlichen Betrag |V*| = 1 aufweist, ergibt das Integral der Kurve 1/x für den gleichen Bereich den unendlich großen Wert A = ∞.
Der Vergleich zwischen der "Fläche" A (unter der Hyperbel y = 1/x) und dem Betrag |V*| erinnert daran, dass das Volumen dieses um die x-Achse (mit x → ∞) rotierenden Segments A den Wert π annimmt.
Die Schnittfläche des Rotationskörpers an der Stelle x hat die Größe einer Kreisfläche πy² = π(1/x)² (6). Das Rotationsvolumen der unendlich großen Fläche A im Bereich x = 1 … ∞ ist
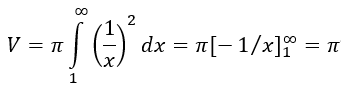
Physikalisch betrachtet, wandelt die Einführung eines neuen Freiheitsgrades, der Rotation, den Wert Unendlich zu einem endlichen Wert.
"Rotation" bedeutet in diesem Falle zwei neue zusätzlichen Dimensionen quer zur x-Achse.
Das gleiche gilt natürlich auch aus Gründen der Symmetrie für eine Fläche zwischen Hyperbelast und y-Achse, welche um die y-Achse rotiert.
Die Krümmung F'' ist ein Maß dafür, wie stark sich die Tangente an einem Kurvenpunkt ändert. Die Hyperbelkurve wird mit wachsendem x immer flacher.(6a)
Mit fortschreitender Zeitdauer wird die Änderung der Zeit immer geringerer und so zu einem kontinuierlichen Zeitfluss. Zeitdauer und Distanz wachsen kontinuierlich ohne Grenze gegen Unendlich.
Dies gilt jedoch nur für eine 1-dimensionale Betrachtung.
Für einen 3-dimensionalen (räumlichen) Raum dagegen haben Zeitdauer und Distanz einen endlichen Grenzwert, den Wert π.
Dieser Wert entspricht der Länge eines Kreisumfangs für einen Kreisdurchmesser 1.
Die physikalische Deutung dieses mathematischen Zusammenhangs für π als Grenzwert bleibt im Moment noch offen und bedarf der weiteren Diskussion.
So entdeckte Hawking, dass die Menge der Informationen nicht von einem Volumen abhängt, sondern von der Oberfläche, die den Raum umgibt. Das würde für unseren Fall bedeuten, dass in einer unendlichen Zeit und einem unendlichen dreidimensionalen Raum die Informationsmenge gegen unendlich wachsen würde, obwohl das Bezugsvolumen der Information endlich bliebe.
Das könnte von Bedeutung sein, wenn das physikalische Universum als reine Information interpretiert würde.
Gruß, Otto
(6) Das Rotationsvolumen des Hyperbelsegments mit der Schnittfläche 1 ist
Das Volumen beträgt in diesem Falle ca. das Doppelte des Zahlenwertes der Fläche.
(6a) Der Kehrwert der Krümmung wird als Krümmungsradius bezeichnet. Der Krümmungsradius steht immer senkrecht auf der Kurve. Für eine Gerade ist die Krümmung Null.
Für die Krümmung ist die Krümmung im Scheitelpunkt am größten und damit der Krümmungsradius am kleinsten.
Redaktionelle Änderung am 7-SEP-2021
Beitrag zuletzt bearbeitet von Otto am 07.09.2021 um 06:37 Uhr.
[Gäste dürfen nur lesen]
|
Otto
Beiträge: 1.246, Mitglied seit 10 Jahren
|
Beitrag Nr. 2363-5
08.06.2021 07:35
|
Otto schrieb in Beitrag Nr. 2363-2:10. Zeitdauer und Distanz als Integral dieser Änderungen lassen sich zweckmäßig in einem doppelt-logarithmischen Koordinatensystem darstellen. Zur graphischen Darstellung von Zeitdauer und Distanz bietet sich ein ln-ln-Plot mit einer Teilung n auf Basis en und der Eulerzahl e = 2.72… als Basis an.
Durch diese Darstellung wird eine Hyperbel im logarithmischen Koordinatensystem zu einer Geraden (3) Die Gerade gilt für jede beliebige Relativgeschwindigkeit, auch für die Lichtgeschwindigkeit.
Doppelt-logarithmische Darstellung
Im Folgenden wird das obige dekadische x-y-Diagramm in ein doppelt-logarithmisches Koordinatensystem überführt.
Anstelle des meist verwendeten dekadischen Logarithmus y = lg(x) wird der natürliche Logarithmus y = ln(x) verwendet. (7)
Die Punkte B und D des x-y-Koordinatensystems werden in dem doppelt-logarithmischen X-Y-Koordinatensystem zu einem gemeinsamen Koordinatenursprung 0(0,0) zusammengeführt.

Bild: Relativbewegung als Maßstabsänderungen von Distanz und Zeitdauer in einem ln-ln-Plot mit der Abszisse X und der Ordinate Y
Das Diagramm im X-Y-Koordinatensystem gilt sowohl für alle Relativgeschwindigkeiten von Objekten mit einem Impuls (Masse mal Geschwindigkeit), als auch für die Lichtgeschwindigkeit c für Photonen ohne Masse, aber verschiedenen Frequenzen.
Auf der Ordinate Y ist die Zeitdauer dargestellt, auf der Abszisse X die (räumliche) Distanz.
Die Geraden im Diagramm beschreiben die Zusammenhänge zwischen Distanz und Zeitdauer, sowohl für eine Unterlichtgeschwindigkeit v als auch für eine theoretisch mögliche Überlichtgeschwindigkeit.
Für eine Lichtgeschwindigkeit mit dem Wert c = 1 stellt die Gerade Y = 1 – X den aktuellen Licht-Vorkegel (der absoluten Vergangenheit) zum Zeitpunkt Y = 1 dar. Die Gerade Y = 2 – X präsentiert den Ereignishorizont zu dem zukünftigen Zeitpunkt Y = 2 und die Gerade Y = 1 + X stellt den zukünftigen Lichthorizont (Nachkegel der absoluten Zukunft) dar . (8)
Zum Zeitpunkt Y des Urknalls wird der Licht-Nachkegel zum Teilchenhorizont. Der Teilchenhorizont ist der kosmische Lichthorizont, der die maximale Entfernung des beobachtbaren Universums begrenzt.
Die Kurve des Lichtkegels resultiert aus der logarithmischen X-Y-Darstellung der Hyperbel y = 1/x im x-y-Diagramm.
Diese Hyperbel wird im X-Y-Diagramm zu
und für den gegenwärtigen Zeitpunkt (now) Y = 1 die blau dargestellte Gerade
Diese Gerade im logarithmischen X-Y-Diagramm interpretiert die Hyperbel des dekadischen x-y-Diagramms als aktuellen Lichthorizont (Vorkegel).
Die rot dargestellte Gerade Y = 1 + X, der zukünftige Lichtkegel (Nachkegel der absoluten Zukunft), ist die Spiegelung des (blauen) Lichthorizonts Y = 1 – X an der Gegenwart Y = 1.
Diese Spiegelung erfolgt an der Gegenwart (now), also am Ist-Zustand!
Die Zukunft wird allein durch den Ist-Zustand (mit seiner Geschichte) bestimmt.
Bisher wurde vereinfachend S0/F0 = 1 gesetzt.
Für andere Werte S0/F0 ≠1 ändern sich nur die Maßstäbe X und Y. Die Kurven selbst ändern sich dabei nicht.
Die physikalische Wirkung S0 [Js] ist definiert als das Produkt von Energie mal Zeit bzw. Länge mal Impuls. Die energetische Optimierung der Bewegung eines Punktes auf der Weltenlinie erfolgt durch die Änderung der Geschwindigkeitsrichtung oder des Betrages der Geschwindigkeit. Es ändert sich also der Impulsvektor.
Für eine konstante Masse m (oder m = 1) ist demzufolge die physikalische Wirkung S0 proportional der Geschwindigkeit v des Massepunktes.
Für ein masseloses Photon, bestimmt durch die Werte von Energie und Impuls, ist die physikalische Wirkung S0 proportional zur Frequenz ω.
Wird der Maßstab der Ordinate zum Beispiel durch die alternative Skalierung Y' = 2Y ersetzt, dann werden die Skalenpunkte 1, 2, 3, … zu Y'-Punkten 2, 4, 6, … .
Infolge dieser Maßstabsänderung der Skala auf Y' wird doppelt so viel Zeit zum Zurücklegen der (konstanten) Strecke benötigt. Die ursprüngliche Geschwindigkeit wird auf den Wert v/2 halbiert.
Natürlich kann auch der Maßstab der Abszisse verändert werden.
Wird zum Beispiel der Maßstab der Abszisse auf X' = 2X verändert, dann wird in der gleichen Zeitdauer die doppelte Wegstrecke zurückgelegt. Durch diese Maßstabänderung wird die ursprüngliche Geschwindigkeit v auf 2v verdoppelt.
Die Geschwindigkeit, als das Verhältnis von Weg zu Zeit, wird so zu einem Verhältnis zweier Maßstäbe.
Die Veränderung des Maßstabes, das heißt der Skalierung, ist nichts anderes als eine Koordinatentransformation.
Die Beziehung zwischen v und c nach der SRT findet hier in dieser Darstellung keine Berücksichtigung, da sowohl im x-y-Diagramm als auch im X-Y-Diagramm nur die Beziehungen zwischen Zeit und Weg bzw. Distanz und Zeitdauer dargestellt sind und nicht die Beziehungen zwischen zwei verschiedenen Geschwindigkeiten.
Das Verhältnis der Maßstäbe von zwei Geschwindigkeiten v1 und v2 ist
Legen zwei Objekte mit verschiedenen Geschwindigkeiten v1 und v2 die gleiche Entfernung X1 =X2 zurück, dann ist das Verhältnis der Zeitmaßstäbe
Diese Beziehungen zwischen unterschiedlichen Zeitmaßstäben für zwei unterschiedliche Abweichungen v1 und v2 von der Lichtgeschwindigkeit c haben die gleiche Eigenschaft wie die bekannte Eigenzeiten τ eines bewegten Objektes und der Eigenzeit t des "ruhenden" Beobachters.
Für das bewegte Objekt hat sich der Zeitmaßstab mit der fortlaufenden Zeit anders logarithmisch als der Zeitmaßstab des Beobachters verändert.
Es ändert sich also eigentlich mathematisch nicht die Entfernung.
Wir erleben es nur so und beschreiben die Differenz der unterschiedlichen Eigenzeiten als Geschwindigkeit.
Für den Zustand der Ruhe v1 = v2 haben Beobachte und beobachtetes Objekt die gleiche Eigenzeit.
Abweichungen von der Lichtgeschwindigkeit lassen sich mit den Gleichungen wie folgt schreiben:
Ist v1 = c und v2 = v eine Relativgeschwindigkeit kleiner als die Lichtgeschwindigkeit c, dann ist
Die Zeitdauer Yc , die das Licht braucht, um eine feste Strecke zurück zu legen, ist nach der SRT immer kürzer als die Zeitdauer, die für eine Geschwindigkeit v < c benötigt wird.
Deshalb ist Yc/Yv immer kleiner als 1.
Der Zustand der Lichtgeschwindigkeit c ist in diesem Sinne ein "Normal-Zustand"..
Erst die Abweichung von c ist dann eine Bewegung, verbunden mit einer räumlichen Dimension.
Roger Penrose beschreibt diesen Normal-Zustand so, dass die Lichtgeschwindigkeit c deshalb als Naturkonstante ihren physikalischen Sinn verliert.
Die Abweichung vom Normalzustand (v/c) = 1 lässt sich mathematisch auch durch den Ausdruck [1 – (v/c)] beschreiben.
Die Abweichung [1 – (v/c)] ist minimal für v → 0, gleichbedeutend mit Yv → ∞. Die Zeitskala dehnt sich so, als würde die Zeit bei der Lichtgeschwindigkeit stehen bleiben.
Da in unserer erlebten Realität alles einer Zustandsänderung unterliegt, gibt es keine 100-prozentige Abweichung von der Lichtgeschwindigkeit.
Das entspricht dem Verständnis, dass die Lichtgeschwindigkeit in der Praxis nicht erreichbar ist.
Eine alternative mathematische Formulierung für die Abweichung von v = c wäre natürlich auch der Ausdruck [1 – (v/c)²], wie von der SRT her bekannt und geschrieben als (1/ γ)² = 1 – (v/c)².
Der γ-Faktor der SRT lässt sich demzufolge auch als Verhältnis verschiedener Zeit-Maßstäbe formulieren.
Es ist noch der alternative Fall zu beschreiben, dass sich der Entfernungsmaßstab ändert, während der Maßstab für die Zeitdauer konstant ist.
Legen zwei Objekte mit verschiedenen Geschwindigkeiten in der gleichen Zeit Y1 =Y2 unterschiedliche Strecken zurück dann ist das Verhältnis der Entfernungsmaßstäbe
und
und somit
Xv ist kleiner als die durch die Lichtgeschwindigkeit zurückgelegte Strecke Xc.
Deshalb ist auch hier für v < c das Verhältnis der zurückgelegten Strecken Xv/Xc < 1.
Ändern sich die beiden Maßstäbe für Zeit und Raum im gleichen Maße, dann hat das auf die Relativgeschwindigkeit v = X/Y keinen Einfluss. Einen Raum, der expandiert oder komprimiert oder pulsiert würde man nicht bemerken.
Gruss, Otto
(7) Auf Grund der Wahl des natürlichen Logarithmus anstelle des üblichen dekadischen Logarithmus weist dieses spezielle X-Y-Koordinatensystem einige Besonderheiten auf:
- Im lg-Koordinatensystem ist der Koordinatenursprung (0,0) nicht definiert, weil der Wert lg(0) nicht existiert.
- Im ln-Koordinatensystem ist dagegen der Koordinatenursprung (0,0) mit x(D) und y(B) wohl definiert. Die Bereiche x = 0…<1 und y = 0…<1 werden ausgeblendet.
- Bei der lg-Skalierung bilden die Potenzen n der Potenzfunktion 10n die Zahlen der Skalierung. Der Abstand zwischen den Werten von n beträgt 10n (10, 100, 1000, …)
- Bei einer ln-Skalierung bilden die Potenzen n der Potenzfunktion en die Zahlen der Skalierung. Der Abstand zwischen den Werten von n beträgt en (e1, e2, e3, …)
(8) Ein ähnliches Diagramm ist bei "ScienceBlogs" mit dem Titel "Das zyklische Universum des Sir Roger Penrose" zu finden. In dem dort gezeigten Diagramm "Commoving Distance" / "Conformal Time" für die Expansion des Universums ist die Ordinate die Zeit (auf der rechten Seit des Bildes) mit einem logarithmischen Skalenfaktor dargestellt, die Entfernung auf der Abszisse ist dekadisch skaliert.
Siehe die Publikation von Aldemarin vom 9-Sep-2019:
https://scienceblogs.de/alpha-cephei/2019/09/09/ccc...
Redaktionelle Änderung am 7-SEP-2021
Beitrag zuletzt bearbeitet von Otto am 07.09.2021 um 06:45 Uhr.
[Gäste dürfen nur lesen]
|
Okotombrok
Beiträge: 1.477, Mitglied seit 16 Jahren
|
Beitrag Nr. 2363-6
09.06.2021 22:28
|
Hallo Otto,
anspruchsvolles Thema anspruchsvoll aufgearbeitet.
Ich habe alles einmal überflogen und bin sehr interessiert.
Da ich ab morgen für eine Woche endlich wieder einmal Urlaub machen werde und ich nicht weiß,
ob ich in der Zeit Zugriff auf das Internet habe, kann eine intensivere Beschäftigung mit deinem Beitrag noch ein paar Tage dauern.
Als Einstieg in das Thema mag nachstehendes Video hilfreich sein.
Es behandelt keine neuen Ideen, sondern stellt die Problematik der Entfernungsmessung im Universum und deren Interpretation bzw. deren Bedeutung dar.
Es werden unterschiedliche Methoden der Entfernungsmessungen weit entfernter Galaxien beschrieben und festgestellt,
dass bei relativ kurzen Entfernungen, z.B. innerhalb unseres Galaxienhaufens, identische Ergebnisse ermittelt werden,
bei größeren Entfernungen sich aber signifikannte Unterschiede ergeben.
Auch die "mitbewegte Entfernung" wird angesprochen und festgestellt, dass sie im Gegensatz zu Messungen,
die auf Lichtlaufzeiten, Leuchtichteverluste, Zeitdilatationen und Rotverschiebungen fußen, nicht die Entfernung,
wie sie vor mehreren Milliarden Jahren bestanden haben, sondern die heutige aktuelle Entfernung beschreibt.
Andreas Müller - Entfernungen
bis bald
okotombrok"Der Kopf ist rund, damit die Gedanken die Richtung wechseln können"
(Francis Picabia)
anspruchsvolles Thema anspruchsvoll aufgearbeitet.
Ich habe alles einmal überflogen und bin sehr interessiert.
Da ich ab morgen für eine Woche endlich wieder einmal Urlaub machen werde und ich nicht weiß,
ob ich in der Zeit Zugriff auf das Internet habe, kann eine intensivere Beschäftigung mit deinem Beitrag noch ein paar Tage dauern.
Als Einstieg in das Thema mag nachstehendes Video hilfreich sein.
Es behandelt keine neuen Ideen, sondern stellt die Problematik der Entfernungsmessung im Universum und deren Interpretation bzw. deren Bedeutung dar.
Es werden unterschiedliche Methoden der Entfernungsmessungen weit entfernter Galaxien beschrieben und festgestellt,
dass bei relativ kurzen Entfernungen, z.B. innerhalb unseres Galaxienhaufens, identische Ergebnisse ermittelt werden,
bei größeren Entfernungen sich aber signifikannte Unterschiede ergeben.
Auch die "mitbewegte Entfernung" wird angesprochen und festgestellt, dass sie im Gegensatz zu Messungen,
die auf Lichtlaufzeiten, Leuchtichteverluste, Zeitdilatationen und Rotverschiebungen fußen, nicht die Entfernung,
wie sie vor mehreren Milliarden Jahren bestanden haben, sondern die heutige aktuelle Entfernung beschreibt.
Andreas Müller - Entfernungen
bis bald
okotombrok
Signatur:
(Francis Picabia)
[Gäste dürfen nur lesen]
|
Otto
Beiträge: 1.246, Mitglied seit 10 Jahren
|
Beitrag Nr. 2363-7
10.06.2021 04:57
|
Okotombrok schrieb in Beitrag Nr. 2363-6:Auch die "mitbewegte Entfernung" wird angesprochen und festgestellt, dass sie im Gegensatz zu Messungen,
die auf Lichtlaufzeiten, Leuchtichteverluste, Zeitdilatationen und Rotverschiebungen fußen, nicht die Entfernung,
wie sie vor mehreren Milliarden Jahren bestanden haben, sondern die heutige aktuelle Entfernung beschreibt.
Andreas Müller - Entfernungen
Hallo Okotombrok,
Vielen Dank für Deinen interessanten Link.
Dieses Video geht auf die verschiedenen Arten der Entfernungsmessungen im Kosmos ein, die für in der Nähe befindlichen Objekte fast identische Entfernungsmaße ergeben, aber für weiter entfernte Objekte große Unterschiede, je nach Messmethode, aufweisen wie
- der mitbewegte Entfernung,
- der Leuchtkraft-Entfernung,
- der Winkel-Entfernung,
- der Lichtlauf-Entfernung.
Ein schöner Vergleich der Messmethoden-Ergebnisse wird in der Minute 25 des Videos gezeigt.
Mein Beitrag geht auf diese kosmologischen Messmethoden nicht ein.
Ich habe mir nur eine ganz einfache Frage gestellt:
Ist die Laufzeitentfernung das Resultat einer Entfernungs-Änderung oder ist sie das Resultat einer Zeit-Änderung?
Dazu kommt die zweite Frage:
Wann führen die beide (theoretisch möglichen) Ursachen zum gleichen Ergebnis?
Die Antwort führt zu der simplen Gleichung ds∙dt = 1
Die Änderung der Entfernung ds ist gleich dem Kehrwert der Änderung der Zeit dt.
Die Hyperbel ds∙dt = 1 beschreibt die enge Verbindung zwischen Zeit und Raum und lässt eine mögliche Erklärung der Ursache einer räumlichen Dimension zu.
Der Ausdruck dt meint hier eine Veränderung der Zeit selbst und nicht die differentielle Änderung eines Zustandes mit der Zeit (wie sonst üblich v = s' = ds/dt).
Die Zeit wird im Sprachgebrauch als Folge von Augenblicken verstanden, wobei der Abstand zwischen den Augenblicken konstant angenommen wird (konstanter Zeitfluss).
Ich analysiere dagegen den Fall, wenn sich nur der Abstand zwischen den zeitlichen Augenblicken ändert und nicht die Entfernung.
Die Variable "Zeit" weist mit dieser Annahme einen Gradienten auf.
Unter diesem Betrachtungswinkel werden Entfernung und Entfernungsänderung zu einer Art "optischen Täuschung" unserer Erlebniswelt.
Gruß, Otto
Beitrag zuletzt bearbeitet von Otto am 10.06.2021 um 13:21 Uhr.
[Gäste dürfen nur lesen]
|
Harti
Beiträge: 1.644, Mitglied seit 16 Jahren
|
Beitrag Nr. 2363-8
11.06.2021 10:25
|
Hallo Otto,
ich habe deine Ausführungen mit Interesse gelesen und mir auch den Vortrag von Andreas Müller angesehen.
Meine mathematischen Kenntnisse sind allerdings nicht ausreichend, um alles zu verstehen.
Ich habe deshalb eine wesentliche einfachere Vorstellung wie man zu einem Wert 1 der Lichtgeschwindigkeit in der SRT kommt.
Geschwindigkeit ist als Beziehung zwischen Strecke (Raum) und Zeit definiert. Eine solche Beziehung hat immer dann den Wert 1, wenn, als Quotient betrachtet, Zähler und Nenner gleichwertig angenommen werden. Die Einheiten für die Betrachtung von Bewegungen kann man beliebig wählen. Gleichwertigkeit für Strecke und Zeit erhält man, indem man als Längenmaß eine Einheit wählt, die das Licht genau in der Einheit der Zeit zurücklegt, also z.B. Jahr und Lichtjahr. In einem kartesischen Koordinatensystem ergibt sich dann für die Geschwindigkeit des Lichts eine Gerade, die in einem 45°-Winkel verläuft.
Werte unter 1, der Zeitraum ist größer als die Strecke, bedeuten Unterlichtgeschwindigkeit, Werte über 1, die Strecke ist größer als der Zeitraum, bedeuten Überlichtgeschwindigkeit. Die Lichtgeschwindigkeit (der Elektromagnetismus) ist auch bei dieser Darstellung eine naturgegebene Grenze unserer Bewegungs- und Wahrnehmungsmöglichkeiten.
Diese geometrische Darstellung entspricht m.E. der SRT am besten, weil die Lichtgeschwindigkeit (der Elektromagnetismus) die einzige naturgegeben Grundlage der Theorie ist und als absolut vorgestellt wird. Raum und Zeit werden im Gegensatz zu Newton`s Annahmen nicht mehr absolut vorgestellt.
Masse/Energie und daraus folgend Gravitation bleiben in der SRT unberücksichtigt.
Das Relativitätsprinzip, das ebenfalls als Grundlage der SRT genannt wird, ist eine Vorstellung, also keine Naturerscheinung, die eine konkrete Betrachtung des Naturgeschehens von einem Standpunkt (Bezugssystem) aus vermeidet und damit allein Beziehungen in den Blick nimmt. Messungen sind z.B. auf der Grundlage des Relativitätsprinzips nicht möglich, dazu muss ich immer ein Bezugssystem festlegen.
MfG
HartiWichtig ist, dass man nicht aufhört zu fragen. A.E.
ich habe deine Ausführungen mit Interesse gelesen und mir auch den Vortrag von Andreas Müller angesehen.
Meine mathematischen Kenntnisse sind allerdings nicht ausreichend, um alles zu verstehen.
Ich habe deshalb eine wesentliche einfachere Vorstellung wie man zu einem Wert 1 der Lichtgeschwindigkeit in der SRT kommt.
Geschwindigkeit ist als Beziehung zwischen Strecke (Raum) und Zeit definiert. Eine solche Beziehung hat immer dann den Wert 1, wenn, als Quotient betrachtet, Zähler und Nenner gleichwertig angenommen werden. Die Einheiten für die Betrachtung von Bewegungen kann man beliebig wählen. Gleichwertigkeit für Strecke und Zeit erhält man, indem man als Längenmaß eine Einheit wählt, die das Licht genau in der Einheit der Zeit zurücklegt, also z.B. Jahr und Lichtjahr. In einem kartesischen Koordinatensystem ergibt sich dann für die Geschwindigkeit des Lichts eine Gerade, die in einem 45°-Winkel verläuft.
Werte unter 1, der Zeitraum ist größer als die Strecke, bedeuten Unterlichtgeschwindigkeit, Werte über 1, die Strecke ist größer als der Zeitraum, bedeuten Überlichtgeschwindigkeit. Die Lichtgeschwindigkeit (der Elektromagnetismus) ist auch bei dieser Darstellung eine naturgegebene Grenze unserer Bewegungs- und Wahrnehmungsmöglichkeiten.
Diese geometrische Darstellung entspricht m.E. der SRT am besten, weil die Lichtgeschwindigkeit (der Elektromagnetismus) die einzige naturgegeben Grundlage der Theorie ist und als absolut vorgestellt wird. Raum und Zeit werden im Gegensatz zu Newton`s Annahmen nicht mehr absolut vorgestellt.
Masse/Energie und daraus folgend Gravitation bleiben in der SRT unberücksichtigt.
Das Relativitätsprinzip, das ebenfalls als Grundlage der SRT genannt wird, ist eine Vorstellung, also keine Naturerscheinung, die eine konkrete Betrachtung des Naturgeschehens von einem Standpunkt (Bezugssystem) aus vermeidet und damit allein Beziehungen in den Blick nimmt. Messungen sind z.B. auf der Grundlage des Relativitätsprinzips nicht möglich, dazu muss ich immer ein Bezugssystem festlegen.
MfG
Harti
Signatur:
Beitrag zuletzt bearbeitet von Harti am 12.06.2021 um 11:18 Uhr.
[Gäste dürfen nur lesen]
|
Otto
Beiträge: 1.246, Mitglied seit 10 Jahren
|
Beitrag Nr. 2363-9
12.06.2021 22:53
|
Hallo Harti,
Darauf bin ich jedoch in diesem Thread nicht weiter eingegangen.
Ergänzung:
Ich habe mich in diesem Thread mit der Frage beschäftigt, ob die Zeit eine variable Größe ist und einen Gradienten aufweist.
Allgemeiner formuliert:
Liegt die Raumzeit nur im Auge von uns als Betrachter?
Ist unsere Erlebniswelt die objektive Realität und Wahrheit?
Gruß, Otto
Ja, das ist eine übliche und zweckmäßige Annahme, die ich auch benutzt habe.Harti schrieb in Beitrag Nr. 2363-8:Eine solche Beziehung hat immer dann den Wert 1, wenn, als Quotient betrachtet, Zähler und Nenner gleichwertig angenommen werden.
undOtto schrieb in Beitrag Nr. 2363-5:Bisher wurde vereinfachend v = 1 bzw. c = 1 gesetzt.
Otto schrieb in Beitrag Nr. 2363-3:Wird vereinfachend v0 = 1 gesetzt (analog Lichtgeschwindigkeit c = 1), dann ist die Änderung des Wegmaßstabes der Änderung des Zeitmaßstabes umgekehrt proportional (Längendilatation = 1/Zeitdilatation).
Ich halte die LG durchaus für eine variable Größe (wie Max von Laue).Harti schrieb in Beitrag Nr. 2363-8:Diese geometrische Darstellung entspricht m.E. der SRT am besten, weil die Lichtgeschwindigkeit (der Elektromagnetismus) die einzige naturgegeben Grundlage der Theorie ist und als absolut vorgestellt wird.
Darauf bin ich jedoch in diesem Thread nicht weiter eingegangen.
Ergänzung:
Ich habe mich in diesem Thread mit der Frage beschäftigt, ob die Zeit eine variable Größe ist und einen Gradienten aufweist.
Allgemeiner formuliert:
Liegt die Raumzeit nur im Auge von uns als Betrachter?
Ist unsere Erlebniswelt die objektive Realität und Wahrheit?
Gruß, Otto
Beitrag zuletzt bearbeitet von Otto am 12.06.2021 um 23:03 Uhr.
[Gäste dürfen nur lesen]
|
Otto
Beiträge: 1.246, Mitglied seit 10 Jahren
|
Beitrag Nr. 2363-10
07.09.2021 07:34
|
Tipp:
Ich habe meine Beiträge Beitrag Nr. 2363-2 bis Beitrag bis Beitrag Nr. 2363-5 redaktionell überarbeitet.
Hinweise von Claus habe habe ich berücksichtigt.
In Vorbereitung sind neue Kommentare zu den Themen:
- Maßstabsänderung und Entstehung des Universums,
- Rotverschiebung infolge Maßstabsänderung,
- Elektromagnetische Strahlung und Maßstabsänderung,
- Wirkungsquantum der Relativgeschwindigkeit (im Unterschied zum planckschen Wirkungsquantum ℎ = Emin∙T für elektromagnetische Wellen),
- Energiepaket der Relativgeschwindigkeit,
- Wellen (Licht, Strahlungen) - als Funktion einer veränderlichen Zeit ("conformal time") und einer veränderlichen Längendimension ("commoving distance").
Gruß, Otto
Ich habe meine Beiträge Beitrag Nr. 2363-2 bis Beitrag bis Beitrag Nr. 2363-5 redaktionell überarbeitet.
Hinweise von Claus habe habe ich berücksichtigt.
In Vorbereitung sind neue Kommentare zu den Themen:
- Maßstabsänderung und Entstehung des Universums,
- Rotverschiebung infolge Maßstabsänderung,
- Elektromagnetische Strahlung und Maßstabsänderung,
- Wirkungsquantum der Relativgeschwindigkeit (im Unterschied zum planckschen Wirkungsquantum ℎ = Emin∙T für elektromagnetische Wellen),
- Energiepaket der Relativgeschwindigkeit,
- Wellen (Licht, Strahlungen) - als Funktion einer veränderlichen Zeit ("conformal time") und einer veränderlichen Längendimension ("commoving distance").
Gruß, Otto
[Gäste dürfen nur lesen]
|
Harti
Beiträge: 1.644, Mitglied seit 16 Jahren
|
Beitrag Nr. 2363-11
15.09.2021 09:47
|
Hallo Otto,
Man kann die Darstellung der Bewegung von Photonen (Lichtgeschwindigkeit) in einem Weg-/Zeitdiagramm oder Raumzeitdiagramm in der Weise durch Festlegung der Einheiten wählen, dass für die Lichtgeschwindigkeit der Wert 1 entsteht bzw. die Weltlinie eines Lichtstrahls in einem 45°-Winkel verläuft.
Dazu ist lediglich die Lichtgeschwindigkeit (der Elektromagnetismus) als entscheidende Grundlage für die Konstruktion des Koordinatensystems anzunehmen.
In einem kartesischen Koordinatensystem entspricht dann einer Zeiteinheit auf der Zeitachse die Strecke auf der Raumachse, die das das Licht in dieser Zeiteinheit zurücklegt,
z.B. einem Jahr ein Lichtjahr.
Man sollte sich allerdings bewusst sein, dass in Raumzeitdiagrammen der Begriff Geschwindigkeit im Sinne von Strecke pro Zeit, also auch der Begriff Lichtgeschwindigkeit, nicht passt, weil Geschwindigkeit ein Beziehung zwischen Zeit und Raum beinhaltet, also eine Trennung von beiden, während eine raumzeitliche Darstellung auf einer Vereinheitlichung von Zeit und Raum beruht.
MfG
HartiWichtig ist, dass man nicht aufhört zu fragen. A.E.
Otto schrieb in Beitrag Nr. 2363-1:In einem Koordinatensystem mit der mitbewegten Entfernung auf der X-Achse und der konformen Zeit auf der Y-Achse, wird dann die Weltlinie eines Lichtstrahls zu einer Geraden Y = X (das heißt eines um 45° "winkeltreu" geneigten Strahls).
Man kann die Darstellung der Bewegung von Photonen (Lichtgeschwindigkeit) in einem Weg-/Zeitdiagramm oder Raumzeitdiagramm in der Weise durch Festlegung der Einheiten wählen, dass für die Lichtgeschwindigkeit der Wert 1 entsteht bzw. die Weltlinie eines Lichtstrahls in einem 45°-Winkel verläuft.
Dazu ist lediglich die Lichtgeschwindigkeit (der Elektromagnetismus) als entscheidende Grundlage für die Konstruktion des Koordinatensystems anzunehmen.
In einem kartesischen Koordinatensystem entspricht dann einer Zeiteinheit auf der Zeitachse die Strecke auf der Raumachse, die das das Licht in dieser Zeiteinheit zurücklegt,
z.B. einem Jahr ein Lichtjahr.
Man sollte sich allerdings bewusst sein, dass in Raumzeitdiagrammen der Begriff Geschwindigkeit im Sinne von Strecke pro Zeit, also auch der Begriff Lichtgeschwindigkeit, nicht passt, weil Geschwindigkeit ein Beziehung zwischen Zeit und Raum beinhaltet, also eine Trennung von beiden, während eine raumzeitliche Darstellung auf einer Vereinheitlichung von Zeit und Raum beruht.
MfG
Harti
Signatur:
[Gäste dürfen nur lesen]
|
Otto
Beiträge: 1.246, Mitglied seit 10 Jahren
|
Beitrag Nr. 2363-12
25.09.2021 04:45
|
Hallo Harti,
Das ist richtig.
Das Überraschende ist, dass die Betrachtung des Verhältnisses von Weg zu Zeit als Verhältnis zweier Maßstäbe beschrieben werden kann, was letztendlich zu einer Hyperbel führt.
Eine Hyperbel beschreibt auch den Kern der ART, hier allerdings verursacht durch die Wirkung einer Masse.
Die interessante Frage ist, ob die (eindimensionale) Relativgeschwindigkeit ein Spezialfall der ART mit Mꞌ = G∙M/c² = 0 ist.
Siehe hierzu auch die ursprüngliche Gleichung der ART im Beitrag Nr. 2345-91.
Für die SRT ist die Anwendung eines veränderlichen Maßstabes für Zeit und Dimension sehr einfach.
Der veränderliche Maßstab hat überhaupt keine Bedeutung für die Gleichungen der SRT.
Siehe hierzu die Bilder im Beitrag Nr. 2264-641 und Beitrag Nr. 2323-32 .
Durch Multiplikation mit einem Faktor der Längen der Dreiecke ändern sich nicht die Beziehungen für Streckenabschnitte, Längen und die Eigenzeit.
Durch die Maßstab-Faktoren werden nur die Größe der Dreiecke vergrößert/verkleinert.
Gruß, Otto
Harti schrieb in Beitrag Nr. 2363-11:Man sollte sich allerdings bewusst sein, dass in Raumzeitdiagrammen der Begriff Geschwindigkeit im Sinne von Strecke pro Zeit, also auch der Begriff Lichtgeschwindigkeit, nicht passt, weil Geschwindigkeit ein Beziehung zwischen Zeit und Raum beinhaltet, also eine Trennung von beiden, während eine raumzeitliche Darstellung auf einer Vereinheitlichung von Zeit und Raum beruht.
Das ist richtig.
Das Überraschende ist, dass die Betrachtung des Verhältnisses von Weg zu Zeit als Verhältnis zweier Maßstäbe beschrieben werden kann, was letztendlich zu einer Hyperbel führt.
Otto schrieb in Beitrag Nr. 2363-5:Die Geschwindigkeit, als das Verhältnis von Weg zu Zeit, wird so zu einem Verhältnis zweier Maßstäbe.
v = X/Y
Die Veränderung des Maßstabes, das heißt der Skalierung, ist nichts anderes als eine Koordinatentransformation.
Eine Hyperbel beschreibt auch den Kern der ART, hier allerdings verursacht durch die Wirkung einer Masse.
Die interessante Frage ist, ob die (eindimensionale) Relativgeschwindigkeit ein Spezialfall der ART mit Mꞌ = G∙M/c² = 0 ist.
Siehe hierzu auch die ursprüngliche Gleichung der ART im Beitrag Nr. 2345-91.
Für die SRT ist die Anwendung eines veränderlichen Maßstabes für Zeit und Dimension sehr einfach.
Der veränderliche Maßstab hat überhaupt keine Bedeutung für die Gleichungen der SRT.
Siehe hierzu die Bilder im Beitrag Nr. 2264-641 und Beitrag Nr. 2323-32 .
Durch Multiplikation mit einem Faktor der Längen der Dreiecke ändern sich nicht die Beziehungen für Streckenabschnitte, Längen und die Eigenzeit.
Durch die Maßstab-Faktoren werden nur die Größe der Dreiecke vergrößert/verkleinert.
Gruß, Otto
Beitrag zuletzt bearbeitet von Otto am 25.09.2021 um 05:01 Uhr.
[Gäste dürfen nur lesen]
|
Berny
Beiträge: 15, Mitglied seit 17 Jahren
|
Beitrag Nr. 2363-13
11.04.2024 18:51
|
Hallo Otto, habe erst heute deine interessante Zusammenfassung gelesen und bin sicher nicht der Einzige in Manus Zeitforum hier, der Dir dafür höchsten Respekt zollt.
Sehe ich ähnlich so und würde in meiner "Modell-Fehler-Methode" eher von einer Natur-Konsens-Tante in zufälligem wie abfälligen Wortverwandtschaftsgraden sprechen.
Allerdings vertrete ich anfangs die einfache Umkehrthese in meinen (über-) und (unter-)organischen Doppelfehlermodellen, dass die kürzeste Verbindung zwischen zwei Punkten "wenigstens zwei Halbkreise" beträgt, denn ansonsten würde ich ja keinen Fehler begehen, der mich besonders interessiert, solange er nicht gegen 0 (=NULL) tendiert.
Ein ganz besonders delikates 'Posthumulat'
kommt mir dabei in den sokratischen Sinn " so Grat ":
Eine jede Erhaltungsgrüße ist Generator als Vervielfältiger GENE-RA-TOR besonderer Symmetrie-GRUPPEN
von (nahezu musterhaft) idealen auto-logisch sich stetig selbst "GUT" verbessender Kategorienfehler-TRUPPEN.
Schöne Grüße an alle.Die Zeit ist die Erinnerungskonstante eines pulsierenden Universums im JETZT.
Otto schrieb in Beitrag Nr. 2363-2:Otto schrieb in Beitrag Nr. 2363-1:Die Idee der mitbewegten Entfernung von Penrose wird auf die "Laufzeit-Entfernung" angewendet und analysiert.
Zusammenfassung - Maßstabsänderung von Raum und Zeit für die Laufzeitentfernung
Die Ergebnisse sind überraschend.
1. Der Zeitfluss ist nicht konstant, sondern eine veränderliche Größe. Über die Zeitdauer verändert sich der Zeitablauf.
Der Maßstab der Zeit folgt dem Logarithmus naturalis.
Die Zeit verläuft kurz nach einem Ereignis anfangs schneller, später langsamer.
2. Die Definition eines Einheitswertes 1 als Maßzahl für die Zeit und der Maßzahl 1 für die räumliche Entfernung lässt sich rein mathematisch begründen (völlig unabhängig von den willkürlich festgelegten Maßstäben wie Urmeter und Atomuhr).
3. Die Raumzeit ist bei jeder Relativbewegung gekrümmt, verursacht durch Energie und Impuls der physikalischen Krümmung.
Merkmal von Licht ist, dass die Krümmungen von Zeit und von räumlicher Dimension gleich sind.
4. Die Krümmungen, als Maß der Änderung, von Zeitdauer und der Distanz gehen mit zunehmender Zeit gegen Null (konstanter Zeitfluss).
Zeitdauer und räumliche Entfernung wachsen gegen Unendlich. Dies gilt allerdings nur für eine 1-dimensionale räumliche Beziehung zwischen Beobachter und Objekt. Für den dreidimensionalen Raum streben Zeit/Entfernung gegen einen endlichen Grenzwert (π).
5. Die Veränderung des Maßstabes, d.h. die Änderung der Skalierung, ist im Grunde nur eine Koordinatentransformation.
Der γ-Faktor der SRT lässt sich als Verhältnis verschiedener Maßstäbe beschreiben.
Es ist γ² = 1/[1 – (Yc/Yv)²] mit den unterschiedlichen Zeitmaßstäben Y für Licht und für eine Relativgeschwindigkeit v bzw. γ² = 1/[1 – (Xv/Xc)²] mit den unterschiedlichen Zeitmaßstäben X der räumlichen Dimension.
6. Die Änderung des Entfernungsmaßstabes und die Änderung des Zeitmaßstabes sind durch eine Hyperbelgleichung miteinander verknüpft.
Der Wert des Krümmungsradius im Scheitelpunkt der Hyperbel ist identisch mit dem Radius bis zum Scheitelpunkt - wie vom Schwarzschildradius her bekannt - hier durch das Energieniveau der physikalischen Wirkung verursacht. Die Krümmung der Zeit, (als Maß der Steigungsänderung der Hyperbel) tritt auch beim Aussenden von masselosen Photonen auf.
Dieser Kreisradius beschreibt in diesem Falle keine Grenze für Information und kausale Zusammenhänge, sondern ist der Spiegel von Zeitdauer und Distanz.
Die Spiegelung erfolgt am Kreisumfang, die das Äußere des Kreises auf das Innere des Kreises abbildet. So werden Zeit und Raum zueinander Spiegelungen ein und desselben.
Zeit und Raum sind zueinander austauschbar.
Die Kreislinie markiert den Ist-Zustand, den Augenblick.
Den Raum erleben wir. Er ist unsere Erlebniswelt.
Zeit erleben wir nicht; Zeit können wir mit keinem unserer Sinnesorgane wahrnehmen. Die Daten einer Zustandsänderung, der Zeit, existiert nur als gespeicherte Information in unserem Gedächtnis.
Signale sind das Ergebnis der Zeit-Veränderung.
7. Die mathematisch-geometrische Spiegelung von Raum und Zeit am Kreis lässt sich auch prosaisch formulieren:
Der Raum ist der "Schatten" der Zeit. Dieser Schatten ist unsere Erlebniswelt.
Diese Interpretation beantwortet die Frage nach einer (möglichen) Ursache von Raum bzw. einer räumlichen Dimension.
Einstein hat in Bezug auf die Raumzeit formuliert: "Zeit und Raum sind nur Methoden, anhand deren wir denken, und keine Bedingung, in der wir leben."
8. Wenn die Zeit Ausdruck einer Zustandsänderung ist, dann gibt es ohne Zustandsänderung keine Zeit.
Die Relativgeschwindigkeit ist eine Zustandsänderung. So, wie sich eine Entfernung ändert, ändert sich bei einer konstanten Geschwindigkeit im gleichen Maße auch die Zeitdauer. Das gilt für jede Relativgeschwindigkeit, einschließlich der Lichtgeschwindigkeit.
Merkmal der Lichtgeschwindigkeit sind identische Maßstäbe für Raum und für Zeit.
Eine Relativgeschwindigkeit v unterscheidet sich von der Lichtgeschwindigkeit c nur durch unterschiedliche Maßstäbe für Raum und für Zeit.
Die Lichtgeschwindigkeit lässt sich als "Normalzustand" unserer Welt verstehen.
Die Relativbewegung ist nur eine Abweichung von diesem Normalzustand.
Roger Penrose ist der Auffassung, dass die Lichtgeschwindigkeit deshalb ihren Sinn als Naturkonstante verliert.
Sehe ich ähnlich so und würde in meiner "Modell-Fehler-Methode" eher von einer Natur-Konsens-Tante in zufälligem wie abfälligen Wortverwandtschaftsgraden sprechen.
Otto schrieb in Beitrag Nr. 2363-2:Die Zustandsänderung der Distanz bzw. des Raumes ist Ausdruck von Zeit und gleichbedeutend mit der Zeit.
Folglich kann infolge der Symmetrie von Zeitdauer und Distanz die Relativgeschwindigkeit zwischen zwei Objekten als die Wirkung unterschiedlicher Eigenzeiten zweier Punkte (2) interpretiert werden.
Der Zeitmaßstab definiert die Eigenzeiten.
Das Resultat sind unterschiedliche Zeitdauern für einen Beobachter und einem dazu relativ bewegten Objekt.
Für das bewegte Objekt ändert sich also eigentlich nicht die Entfernung.
Wir erleben es nur so und definieren die Differenz der unterschiedlichen Eigenzeiten als Relativgeschwindigkeit.
Wir erleben nur die Zeit, interpretieren sie aber als Raum.
10. Zeitdauer und Distanz als Integral dieser Änderungen lassen sich zweckmäßig in einem doppelt-logarithmischen Koordinatensystem darstellen. Zur graphischen Darstellung von Zeitdauer und Distanz bietet sich ein ln-ln-Plot mit einer Teilung n auf Basis en und der Eulerzahl e = 2.72… als Basis an.
Durch diese Darstellung wird eine Hyperbel im logarithmischen Koordinatensystem zu einer Geraden (3)
Die Gerade gilt für jede beliebige Relativgeschwindigkeit, nicht nur für die Lichtgeschwindigkeit.
Für den speziellen Fall der Lichtgeschwindigkeit wird diese Gerade zum bekannten Lichthorizont bzw. Ereignishorizont.
11. Der veränderliche Maßstab der Zeit ist durch unsere logarithmische Erlebniswelt verdeckt.
Unsere Welt ist eigentlich eine logarithmische Welt.
Erst die geometrische Darstellung mittels eines ln-ln-Plots führt zu den bekannten linearen Zusammenhängen von Raum und Zeit (für konstante Relativgeschwindigkeiten), wie wir sie erleben und messen.
12. Der Urknall ist ursächlich eine spontane Änderung der Zeit, die wir als Quelle von Photonen erleben.
Die Rotverschiebung ist Ausdruck der Änderung der Zeit seit dem Urknall. Wir messen die heutige Frequenzverschiebung des Photonen-Impulses und interpretieren sie als Expansion des Raumes.
Die Rotverschiebung wird nicht durch die Expansion des Raumes verursacht, sondern durch die "Alterung" der Zeit.
Gruß, Otto
Am 7-SEP-2021 redaktionell überarbeitet und ergänzt.
Allerdings vertrete ich anfangs die einfache Umkehrthese in meinen (über-) und (unter-)organischen Doppelfehlermodellen, dass die kürzeste Verbindung zwischen zwei Punkten "wenigstens zwei Halbkreise" beträgt, denn ansonsten würde ich ja keinen Fehler begehen, der mich besonders interessiert, solange er nicht gegen 0 (=NULL) tendiert.
Ein ganz besonders delikates 'Posthumulat'
kommt mir dabei in den sokratischen Sinn " so Grat ":
Eine jede Erhaltungsgrüße ist Generator als Vervielfältiger GENE-RA-TOR besonderer Symmetrie-GRUPPEN
von (nahezu musterhaft) idealen auto-logisch sich stetig selbst "GUT" verbessender Kategorienfehler-TRUPPEN.
Schöne Grüße an alle.
Signatur:
Beitrag zuletzt bearbeitet von Berny am 11.04.2024 um 18:52 Uhr.
[Gäste dürfen nur lesen]
In diesem Forum dürfen nur Mitglieder schreiben. Hier kannst du dich anmelden
