Mathematik auf Leben und Tod
Thema erstellt von Suza
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2341-21
19.03.2020 06:20
|
Suza schrieb in Beitrag Nr. 2341-20:Das ist also ein schrittweises Herantasten. Ich hatte mich schon gefragt, wie man alleine durch Zirkelschlag zu dem Punkt bei 1,23 gelangen kann.
Die gleiche Frage hatte sich Otto ja auch gestellt.
Die Gleichung (5) von Claus, Beitrag Nr. 2341-6,
h(x) = 1/sqrt(2² - x²) + 1/sqrt(3² - x²) = 1
ergibt leider keine Parabel, wie das Bild des Rechenergebnisses via "Wolfram Alpha" nahelegt.
Die Kurve ist dagegen U-förmig wie die folgenden geometrischen Darstellungen zeigen.
Beide Summanden von h(x) = f(x) + g(x)
f(x) = 1/sqrt(2² - x²)
g(x) = 1/sqrt(3² - x²)
ergeben ebenfalls U-förmige Kurven.
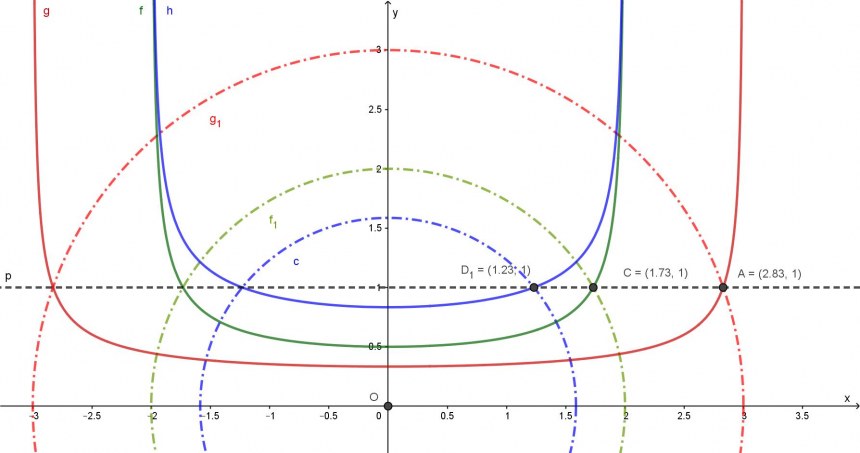
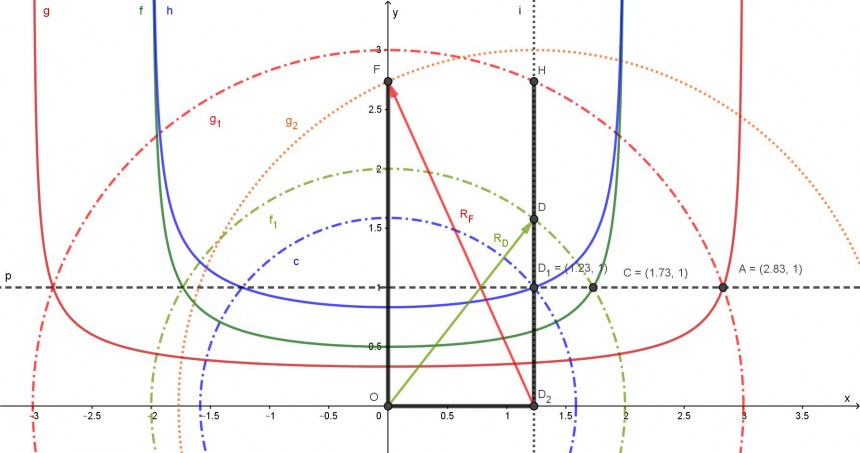
Der Nenner der Gleichungen f(x) und g(x) repräsentiert den Radius von Kreisen.
f1²(x) = 1/f²(x) = 1/(2² - x²) → f1² + x² = 2² → ein Kreis mit dem Radis 2.
g1²(x) = 1/g²(x) = 1/(3² - x²) → g1² + x² = 3² → ein Kreis mit dem Radis 3.
Die Punkte A und C sind die Schnittpunkte der Kurven f(x) und g(x) mit der Geraden y = 1.
Diese beiden Punkte lassen sich mit "Lineal und Zirkel" ermitteln, also jede der Komponenten f(x) und g(x) von h(x) = Gleichung (5).
Das gilt leider nicht für die Gleichung h(x)!
Der Schnittpunkt D1(1.23,1) läßt sich m.E. nicht mit "Lineal und Zirkel" konstruieren! Zumindest habe ich keine Idee.
D1(x = 1.23) = D (x = 1.23) = D2(x = 1.23) = H(x = 1.23) ist die gesuchte Breite des Tanks.
Gruß, Otto
Beitrag zuletzt bearbeitet von Otto am 19.03.2020 um 10:55 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 1.734, Mitglied seit 16 Jahren |
Beitrag Nr. 2341-22
21.03.2020 20:32
|
Otto schrieb in Beitrag Nr. 2341-21:Das gilt leider nicht für die Gleichung h(x)!
Der Schnittpunkt D1(1.23,1) läßt sich m.E. nicht mit "Lineal und Zirkel" konstruieren! Zumindest habe ich keine Idee.
Hallo Otto,
sehr schöne Darstellung!
Bewiesen habe ich es nicht, aber meine analytische Lösung ist ein Polynom 3. Grades und die sind allgemein verwandt mit
dem Winkel-Dreiteilungs-Problem, welches nicht konstruierbar ist. Der Beweis des letzteren wird damit geführt,
dass das entsprechende Polynom 3. Grades im allgemeinen keine Nullstellen in Zahlenkörper hat, der sich
aus der Einheitslänge konstruieren läßt.
Bei dem Konstuktionsansatz von Harald hatte ich gehofft, dass die Hüllkurve der Schar der 3er-Strecken eine Hyperbel sei, ist aber
von höherem Grad und wahrscheinlich auch nicht direkt konstruierbar.
LG
Thomas
Signatur:
[Gäste dürfen nur lesen]
| Beiträge: 936, Mitglied seit 13 Jahren |
Beitrag Nr. 2341-23
21.03.2020 20:58
|
Zitat von Otto:Der Schnittpunkt D1(1.23,1) läßt sich m.E. nicht mit "Lineal und Zirkel" konstruieren! Zumindest habe ich keine Idee.
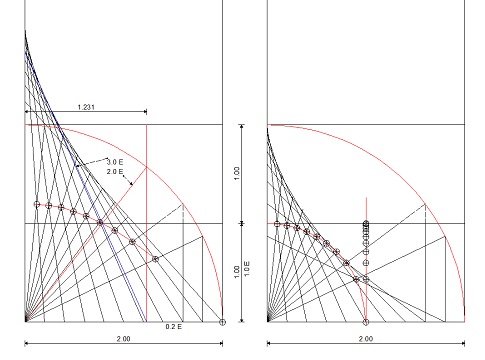
Lösungsversuch: Harald
Meine graphische Lösung ergibt aber die 1.23,1 recht gut. Klar ist, dass man nicht direkt die Lösung mit den Stäben 2E + 3E + 1E Wassertiefe aufreißen kann.
Man darf aber schon bei Fragestellungen die Lösungsmenge als Teil der Lösung die zum Ziel führen kann berücksichtigen.
Dies ist auch graphisch mit Bleistift und Zirkel sowie Lineal möglich.
Liegt der 3er Stab horizontal im Brunnen ist kein Schnittpunkt und keine Wassertiefe messbar. Erst wenn der 2er Stab aus der Horizontalen an der Wand nach oben startet ist mit Schnittpunkten und mit Wassertiefen bei Schnittpunkten 2er x 3er zu rechnen. Ist die Breite des Brunnens etwa Null, kann man nicht mehr von einem Brunnen sprechen und der Schnittpunkt ist ebenfalls nicht mehr zu finden.
Wenn man möchte, kann man den Zwischenbereich – wo die Schnittpunkte die 1er Höhe überspringen noch horizontal aufblasen und so an einer Verfeinerung der Lösungsbreite arbeiten.
SUZA
KURZ – Bereiche in Österreich.
Mit Wolfgang Schüssel saß ich mal geneinsam an einem Tisch und da konnte man gut einsehen,
wie Milliarden an Steuergeldern an die Freunde weitergereicht werden.
Es ist leider nicht möglich – in Österreich als unabhängiger Bauingenieur im Bereich des Bauwesens tätig zu werden.
Baumeister sollte man sein – Heimat bist Du (G)rosser (s)öhne.
An einer Österreichischen Ingenieurschule konnte ich mal eine Rechenaufgabe – es ging ebenfalls um Dreiecke – exakt richtig berechnen. Leider war der Professor anderer Ansicht und meinte: Seine Lösungswege wären die einzig richtigen. Die nachfolgende Mathe - Stunde verwendete er, um zu demonstrieren, dass 1 + 1 eben nicht zwei wären. In Mathe bekam ich dann halt eine Fünf. Nach AUSTRIA – Modus nicht gerade gut. Nach Schweizer Modus schaffte ich dann, ebenfalls an einer Ingenieurschule eine glatte Sechs, sah deutlich, dass die gesamte Bandbreite (auch von Schulnoten) erforderlich ist um Lösungen sicher zu finden.
Mathematik auf Leben und Tod
Harald
Signatur:
ist die Antwort der Gegenwart auf die Einwirkung vergangener Wichtigkeiten.
Beitrag zuletzt bearbeitet von Harald Denifle am 22.03.2020 um 11:00 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2341-24
21.03.2020 21:53
|
Harald Denifle schrieb in Beitrag Nr. 2341-23:Dies ist auch graphisch mit Bleistift und Zirkel sowie Lineal möglich.
Hallo Harald,
Deinen Lösungsvorschlag verstehe ich als Iterartionsprozess, nicht als Konstruktion mittels Geometrie.
Gruß, Otto
[Gäste dürfen nur lesen]
| Beiträge: 936, Mitglied seit 13 Jahren |
Beitrag Nr. 2341-25
22.03.2020 10:47
|
Hallo Otto
Immer wenn wir an der Natur herumrechnen, kommt das Iterative ins Spiel. Es spielt dabei keine Rolle, ob die Lösungen mit Zahlen oder mit graphischen Methoden gesucht werden. Die Variationen aller natürlichen Kennwerte erfordert unser Verständnis für die Variabilität und vor allem für die Gültigkeitsbereiche der Parameter einer sinnvollen Berechnung.
Heute Morgen - noch vor dem Frühstück, konnte man - on TV - sehr interessante Informationen über Leibniz und sein Wirken, auch in mathematischer Hinsicht, erhalten.
Am LRZ – dem Leibniz-Rechenzentrum, wird etwa auch an der globalen Erddynamik rumgerechnet. Da geht vieles nur iterativ und basiert weitestgehend auf Annahmen, weil dann doch recht vieles nicht genau erfassbar ist. Das wussten wir auch schon als die Lösung des Problems mit den HÜGELI im und um den Bodensee gesucht wurde. Darf ich an dieser Stelle aber kaum/nicht erwähnen, da es wohl artgerecht in den Bereich – Hügeli im Bodensee – entsorgt werden müsste. Aber klar ist doch, dass Berechnungen mit unseren Naturbausteinen, stets nur ein iterativer Prozess sein kann.
Mit iterativ meine ich hier die gesamte Bandbreite, welche erfasst und gesehen werden muss.
An der Wasserscheide von Europa stehe ich zusammen mit dem Bauherrn eines Hotelneubaus. Der Neubau muss zur Gänze abgerissen werden, weil die Statik und die Dynamik des Objektes falsch oder genauer gesagt wohl gar nicht berechnet wurde. Der finanzielle Schaden, für diese Familie, beträgt mehr als 5 Millionen Euro und ist durch nichts gedeckt.
Mathematik auf Leben und Tod.
Passt schon zum Thema, da IBIZA und besonders das gesamteuropäische IBIZA
durch ein neues Medienthema in Grund und Boden verschoben werden muss und
politisch gewünscht auch kann.
BAUMEISTER:
Ein gut bekannter Baumeister meinte und teilte es mir persönlich mit:
Er werde innert kürzester Zeit der (g)rösste Baumeister unserer Region sein.
Sein Schwiegervater, ein CEO einer (g)rossen Bank im nahen Ausland würde schon dafür sorgen.
Eingekaufte Politik, reichlich Rechtsanwälte, mindestens ein integrierter Architekt/Ingenieur, eigene Gerüstbauer, alles aus einem Guss und selbst der Fuhrpark – die LOGISTIK wird mit angeschlossener Werkstatt stets auf Hochglanz gehalten. Managergerecht erfolgt die Baukontrolle, welche eigentlich stets unabhängig für fachgerechtes und faires Bauen gegenüber den öffentlichen und den privaten Bauherrschaften sorgen sollte, natürlich über Strohmänner und Strohfrauen geleistet, welche mit normgerechtem, universitärem Fußabdruck, die (G)rössten Controlling - Institute leiten.
Eine Integration in solch einen Baukartell - habe ich gerne abgelehnt.
Trotzdem ist die Lösung mittels konstruktiver Geometrie durchaus lösbar und in den Grenzen der natürlichen Variabilität auch stimmig.
lg HaraldEs gibt nur eine Zeit - die aktive und die passive Gegenwart - und Gravitation
ist die Antwort der Gegenwart auf die Einwirkung vergangener Wichtigkeiten.
Immer wenn wir an der Natur herumrechnen, kommt das Iterative ins Spiel. Es spielt dabei keine Rolle, ob die Lösungen mit Zahlen oder mit graphischen Methoden gesucht werden. Die Variationen aller natürlichen Kennwerte erfordert unser Verständnis für die Variabilität und vor allem für die Gültigkeitsbereiche der Parameter einer sinnvollen Berechnung.
Heute Morgen - noch vor dem Frühstück, konnte man - on TV - sehr interessante Informationen über Leibniz und sein Wirken, auch in mathematischer Hinsicht, erhalten.
Am LRZ – dem Leibniz-Rechenzentrum, wird etwa auch an der globalen Erddynamik rumgerechnet. Da geht vieles nur iterativ und basiert weitestgehend auf Annahmen, weil dann doch recht vieles nicht genau erfassbar ist. Das wussten wir auch schon als die Lösung des Problems mit den HÜGELI im und um den Bodensee gesucht wurde. Darf ich an dieser Stelle aber kaum/nicht erwähnen, da es wohl artgerecht in den Bereich – Hügeli im Bodensee – entsorgt werden müsste. Aber klar ist doch, dass Berechnungen mit unseren Naturbausteinen, stets nur ein iterativer Prozess sein kann.
Mit iterativ meine ich hier die gesamte Bandbreite, welche erfasst und gesehen werden muss.
An der Wasserscheide von Europa stehe ich zusammen mit dem Bauherrn eines Hotelneubaus. Der Neubau muss zur Gänze abgerissen werden, weil die Statik und die Dynamik des Objektes falsch oder genauer gesagt wohl gar nicht berechnet wurde. Der finanzielle Schaden, für diese Familie, beträgt mehr als 5 Millionen Euro und ist durch nichts gedeckt.
Mathematik auf Leben und Tod.
Passt schon zum Thema, da IBIZA und besonders das gesamteuropäische IBIZA
durch ein neues Medienthema in Grund und Boden verschoben werden muss und
politisch gewünscht auch kann.
BAUMEISTER:
Ein gut bekannter Baumeister meinte und teilte es mir persönlich mit:
Er werde innert kürzester Zeit der (g)rösste Baumeister unserer Region sein.
Sein Schwiegervater, ein CEO einer (g)rossen Bank im nahen Ausland würde schon dafür sorgen.
Eingekaufte Politik, reichlich Rechtsanwälte, mindestens ein integrierter Architekt/Ingenieur, eigene Gerüstbauer, alles aus einem Guss und selbst der Fuhrpark – die LOGISTIK wird mit angeschlossener Werkstatt stets auf Hochglanz gehalten. Managergerecht erfolgt die Baukontrolle, welche eigentlich stets unabhängig für fachgerechtes und faires Bauen gegenüber den öffentlichen und den privaten Bauherrschaften sorgen sollte, natürlich über Strohmänner und Strohfrauen geleistet, welche mit normgerechtem, universitärem Fußabdruck, die (G)rössten Controlling - Institute leiten.
Eine Integration in solch einen Baukartell - habe ich gerne abgelehnt.
Zitat von Otto:Deinen Lösungsvorschlag verstehe ich als Iterartionsprozess, nicht als Konstruktion mittels Geometrie.
Trotzdem ist die Lösung mittels konstruktiver Geometrie durchaus lösbar und in den Grenzen der natürlichen Variabilität auch stimmig.
lg Harald
Signatur:
ist die Antwort der Gegenwart auf die Einwirkung vergangener Wichtigkeiten.
Beitrag zuletzt bearbeitet von Harald Denifle am 22.03.2020 um 10:50 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 1.734, Mitglied seit 16 Jahren |
Beitrag Nr. 2341-26
22.03.2020 11:55
|
Harald Denifle schrieb in Beitrag Nr. 2341-25:Zitat von Otto:Deinen Lösungsvorschlag verstehe ich als Iterartionsprozess, nicht als Konstruktion mittels Geometrie.
Trotzdem ist die Lösung mittels konstruktiver Geometrie durchaus lösbar und in den Grenzen der natürlichen Variabilität auch stimmig.
lg Harald
Hallo Harald,
Otto benutzt "konstruierbar" im Sinn der mathematischen Geometrie, der meint, dass man in einer eukidischen Ebene mit exakten Zirkel und Lineal in endlich vielen Schritten exakt zum Ziel kommt.
Signatur:
[Gäste dürfen nur lesen]
| Beiträge: 936, Mitglied seit 13 Jahren |
Beitrag Nr. 2341-27
22.03.2020 14:02
|
Hoi Thomas
Otto und ich gehören schon zur älteren Generation von Ingenieuren. Klar ist, wir wissen schon Beide, von was wir sprechen und es geht nicht um ein RechthaberEi. - im Gegenteil. Wir haben noch gelernt mit Zirkel und Bleistift an gewagte Konstruktionen ranzugehen und schaffen einen rechten Winkel auch ohne GEO – Dreieck in die Landschaft oder auch auf Papier zu setzen.
Wenn SUZA von einem realen Brunnen spricht, dann kann meine Lösung durchaus Berechtigung finden. Klar hat Otto im Sinne einer theoretischen, euklidischen Ebene und vermutlich nur dort ist so eine gedanklich perfekte Ebene zu finden – recht. Für diesen Bereich gibt es aber keine Zirkel und keine Lineale welche diesem hohen Anspruch – variationsfrei zu sein – entsprechen könnten.
lg HaraldEs gibt nur eine Zeit - die aktive und die passive Gegenwart - und Gravitation
ist die Antwort der Gegenwart auf die Einwirkung vergangener Wichtigkeiten.
Otto und ich gehören schon zur älteren Generation von Ingenieuren. Klar ist, wir wissen schon Beide, von was wir sprechen und es geht nicht um ein RechthaberEi. - im Gegenteil. Wir haben noch gelernt mit Zirkel und Bleistift an gewagte Konstruktionen ranzugehen und schaffen einen rechten Winkel auch ohne GEO – Dreieck in die Landschaft oder auch auf Papier zu setzen.
Wenn SUZA von einem realen Brunnen spricht, dann kann meine Lösung durchaus Berechtigung finden. Klar hat Otto im Sinne einer theoretischen, euklidischen Ebene und vermutlich nur dort ist so eine gedanklich perfekte Ebene zu finden – recht. Für diesen Bereich gibt es aber keine Zirkel und keine Lineale welche diesem hohen Anspruch – variationsfrei zu sein – entsprechen könnten.
lg Harald
Signatur:
ist die Antwort der Gegenwart auf die Einwirkung vergangener Wichtigkeiten.
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2341-28
22.03.2020 19:09
|
Harald Denifle schrieb in Beitrag Nr. 2341-25:Trotzdem ist die Lösung mittels konstruktiver Geometrie durchaus lösbar und in den Grenzen der natürlichen Variabilität auch stimmig.
Hallo Harald,
natürlich weiß ich, daß in der Natur fast nur iterative Zustandsänderungen existieren.
All unsere mathematischen Beschreibungen sind nur Näherungen, mit denen wir in der Praxis gut zurecht kommen.
Suza hat aber eine "einfache" Aufgabe der ebenen Geometrie gestellt.
Die Gleichung (5), die Claus aus der Aufgabenstellung abgeleitet hat, benutzt nur Sätze der Geometrie.
Deshalb liegt die Frage nahe, wie eine Konstruktion mit "Lineal und Zirkel" erfolgen könnte.
Das hat nichts mit Iterationen zu tun.
Gruß, Otto
[Gäste dürfen nur lesen]
| Beiträge: 399, Mitglied seit 10 Jahren |
Beitrag Nr. 2341-29
22.03.2020 20:04
|
Otto schrieb in Beitrag Nr. 2341-28:Deshalb liegt die Frage nahe, wie eine Konstruktion mit "Lineal und Zirkel" erfolgen könnte.
Das hat nichts mit Iterationen zu tun.
Wie du hier selber schon gesagt hast: eine echte Konstruktion mit Lineal und Zirkel, bei der durch Zirkelschlag Schnittpunkte auf 1,231 entstehen, wird es nicht geben. Ich schließe mich da voll deiner Auffassung an.
Signatur:
Teilt man aber sein Wissen, hat man hinterher noch genau so viel, der andere aber etwas mehr als vorher.
[Gäste dürfen nur lesen]
| Beiträge: 2, Mitglied seit 4 Jahren |
Beitrag Nr. 2341-30
23.03.2020 22:03
|
Ehrlich gesagt bin ich kein Mathe Fan, aber man kann immer eine Nachhilfe beantragen.Kriechen ist die unwürdigste Art sich fortzubewegen, besonders, wenn man zu Kreuze kriecht.
Signatur:
[Gäste dürfen nur lesen]
| Beiträge: 936, Mitglied seit 13 Jahren |
Beitrag Nr. 2341-31
24.03.2020 19:32
|
Hmmmm – es gibt ja auch diese Zahlenwerte,
welche keine genauen Wertlösungen anzubieten scheinen,
fast leicht lebendig, vorwärtstaumelnd nach der richtigen Lösung suchend
– Schritt für Schritt – ein Cremona Plan für das
Wissen dann doch meist leicht verstaubt?
Harald
H:cool: πEs gibt nur eine Zeit - die aktive und die passive Gegenwart - und Gravitation
πEs gibt nur eine Zeit - die aktive und die passive Gegenwart - und Gravitation
ist die Antwort der Gegenwart auf die Einwirkung vergangener Wichtigkeiten.
welche keine genauen Wertlösungen anzubieten scheinen,
fast leicht lebendig, vorwärtstaumelnd nach der richtigen Lösung suchend
– Schritt für Schritt – ein Cremona Plan für das
Wissen dann doch meist leicht verstaubt?
Harald
H:cool:
 π
πSignatur:
ist die Antwort der Gegenwart auf die Einwirkung vergangener Wichtigkeiten.
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2341-32
03.05.2020 22:25
|
Otto schrieb in Beitrag Nr. 2341-11:Hast Du mal versucht, das Bild von Suza mit "Lineal und Zirkel" nachzuvollziehen?
Wenn Ja, in welchen Schritten (ohne zusätzliche Annahmen, nur mit Daten für A, B und C)?
Siehe neu eröffnetes Thema "Interpretation der Drehung einer Strecke als eine Schwingung/Welle", Beitrag Nr. 2345-1.
Gruß, Otto
[Gäste dürfen nur lesen]
| Beiträge: 5, Mitglied seit 3 Jahren |
Beitrag Nr. 2341-33
02.05.2021 15:14
|
Suza schrieb in Beitrag Nr. 2341-3:Thomas der Große schrieb in Beitrag Nr. 2341-2:Es gibt eine geschlossene Darstellung der Lösung. Also mag es Menschen gegeben haben, die sie fanden.
Wirklich brilliant geschlussfolgert! :smiley8:
Da ich gern verstehen möchte, wie man zu dieser Lösung auf mathematischem Weg gelangen kann, wäre ich an ein paar Details zum Rechenweg sehr interessiert.
Ja defintiv, finde ich auch :-)

[Gäste dürfen nur lesen]
| Beiträge: 1.734, Mitglied seit 16 Jahren |
Beitrag Nr. 2341-34
27.12.2022 20:25
|
Bealeate schrieb in Beitrag Nr. 2341-33:Suza schrieb in Beitrag Nr. 2341-3:Wirklich brilliant geschlussfolgert! :smiley8:
Da ich gern verstehen möchte, wie man zu dieser Lösung auf mathematischem Weg gelangen kann, wäre ich an ein paar Details zum Rechenweg sehr interessiert.
Ja defintiv, finde ich auch :-)
Moin Bealeate!
Die zu lösende Gleichung in einer Variablen hat Claus hergeleitet in Beitrag Nr. 2341-6 .
Die läßt sich in eine Polynom-Gleichung vierten Grades überführen. Der Mathematiker weiss an der Stelle,
dass so eine Gleichung eine geschlossene Lösung hat (im allgemeinen 4 komplexe Lösungen).
Relevant sind die positiv reellen Lösungen; davon gibt es genau eine und die kann man sich bei
Wolfram Alpha ausgeben lassen mit Knopf Exact Form.
Signatur:
Beitrag zuletzt bearbeitet von Thomas der Große am 27.12.2022 um 20:28 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 254, Mitglied seit 10 Jahren |
Beitrag Nr. 2341-35
29.12.2022 09:58
|
In diesem Forum dürfen nur Mitglieder schreiben. Hier kannst du dich anmelden



 Nach oben
Nach oben