Du befindest dich hier: Manus Zeitforum
 Raum und Zeit
Raum und Zeit
 Interpretation der Drehung einer Strecke als eine Schwingung/Welle (Seite 7)
Interpretation der Drehung einer Strecke als eine Schwingung/Welle (Seite 7)
 Raum und Zeit
Raum und Zeit
 Interpretation der Drehung einer Strecke als eine Schwingung/Welle (Seite 7)
Interpretation der Drehung einer Strecke als eine Schwingung/Welle (Seite 7)
Interpretation der Drehung einer Strecke als eine Schwingung/Welle
Thema erstellt von Otto
| Beiträge: 952, Mitglied seit 9 Jahren |
Beitrag Nr. 2345-121
03.06.2020 07:12
|
Hallo, Claus, Otto!
So weit ich informiert bin, hängt die „Lebensdauer“ eines SL von seiner Masse ab - je weniger Masse, desto kürzer die „Lebensdauer“, Für spekulierte SL in Elementarteilchen wäre diese Zeit erstens unmessbar kurz, und zweitens bedeutet das, dass sie nicht existieren können - sie zerfallen quasi instantan.
Gruß Henry
PS: Übrigens würde der Mond nicht wegen der Krümmung der Raumzeit durch die Mondmasse auf die Erde fallen, sondern durch die Krümmung der Erdmasse. SIE zwingt den Mond um seine Umlaufbahn. ::cool: Das Leben ist zu ernst, um es nur ernst zu nehmen.
Das Leben ist zu ernst, um es nur ernst zu nehmen.
So weit ich informiert bin, hängt die „Lebensdauer“ eines SL von seiner Masse ab - je weniger Masse, desto kürzer die „Lebensdauer“, Für spekulierte SL in Elementarteilchen wäre diese Zeit erstens unmessbar kurz, und zweitens bedeutet das, dass sie nicht existieren können - sie zerfallen quasi instantan.
Gruß Henry
PS: Übrigens würde der Mond nicht wegen der Krümmung der Raumzeit durch die Mondmasse auf die Erde fallen, sondern durch die Krümmung der Erdmasse. SIE zwingt den Mond um seine Umlaufbahn. ::cool:

Signatur:
Beitrag zuletzt bearbeitet von Henry-Dochwieder am 03.06.2020 um 07:16 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 1.477, Mitglied seit 16 Jahren |
Beitrag Nr. 2345-122
03.06.2020 07:56
|
Henry-Dochwieder schrieb in Beitrag Nr. 2345-121:Übrigens würde der Mond nicht wegen der Krümmung der Raumzeit durch die Mondmasse auf die Erde fallen, sondern durch die Krümmung der Erdmasse. SIE zwingt den Mond um seine Umlaufbahn
Der Mond wird nicht gezwungen, er fällt einfach nur.:cool:

Signatur:
(Francis Picabia)
[Gäste dürfen nur lesen]
| Beiträge: 952, Mitglied seit 9 Jahren |
Beitrag Nr. 2345-123
03.06.2020 09:05
|
Okotombrok schrieb in Beitrag Nr. 2345-122:Henry-Dochwieder schrieb in Beitrag Nr. 2345-121:Übrigens würde der Mond nicht wegen der Krümmung der Raumzeit durch die Mondmasse auf die Erde fallen, sondern durch die Krümmung der Erdmasse. SIE zwingt den Mond um seine Umlaufbahn
Der Mond wird nicht gezwungen, er fällt einfach nur.:cool:
Nöö, er folgt den Geodäten, hervorgerufen durch die Masse der Erde!
Signatur:
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 2345-124
03.06.2020 09:51
|
Vielleicht würden die Geodäten ihn zu fallen zwingen, wenn er nicht freiwillig folgen würde? :smiley4: Man weiß es nicht.
Man weiß es nicht.
 Man weiß es nicht.
Man weiß es nicht.
[Gäste dürfen nur lesen]
| Beiträge: 952, Mitglied seit 9 Jahren |
Beitrag Nr. 2345-125
03.06.2020 10:29
|
jClaus schrieb in Beitrag Nr. 2345-124:Vielleicht würden die Geodäten ihn zu fallen zwingen, wenn er nicht freiwillig folgen würde? :smiley4:Man weiß es nicht.
Ja, man müsste ihn fragen!
Aber äquivalent ist nicht "das Selbe".
Aber, um es nicht so kryptisch zu lassen - man kann feststellen, ob man sich im Gravitationsfeld oder weit ab von jeder Masse befindet, es ist nicht das Selbe.
Signatur:
Beitrag zuletzt bearbeitet von Henry-Dochwieder am 03.06.2020 um 11:21 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 905, Mitglied seit 7 Jahren |
Beitrag Nr. 2345-126
03.06.2020 12:06
|
Hallo Henry, Claus, Okotombrok und Otto,
hast du, Otto, nicht vielleicht den einen Punkt getroffen, der sich auch zwischen den Gravitationsfeldern von Erde und Mond befinden wird? Es ist nicht ausgeschlossen, dass man diesen Punkt, und nur diesen einen und ebensolchen einen in anderen Fällen, als in Raumzeitgedanken einzig ausgestattet mit der Größe von jeweils Null in Zeit- und Raumeinheiten ansehen kann. Dort heben sich die Gravitationsfelder auf, es herrscht ein Gleichgewicht unter diesen weit wirkenden und von anderen Wirkungen befreiten Kräften und nur dort kann im Universum alles auf Null gesetzt sein.
Zumindest wäre dies meine einzige Idee, Ottos Feststellungen zu interpretieren.
Mathematik und Physik, gerade auch Differential- und Integralrechnung, waren einst meine Leidenschaften, Otto, die mir gründlich vergällt wurden, nachdem ich in meinem im Grunde nur altsprachlich ausgerichteten Gymnasium für Jungs vom eher schon dort verachteten neusprachlichen Zug auf den gerade neu eingerichteten naturwissenschaftlichen Zug wechselte, der sich dann aber mit nur 11 Personen aus 1-3 Jahre älteren Sitzenbleibern auch aus dem Mädchengymnasium meines Wohnortes rekrutierte. Ich habe es danach vorgezogen, mich studienmäßig anders zu orientieren und es nicht bereut. Denken an diese Zeit mag ich allerdings nicht und ebenso wenig erinnert. So sind fast 60 ohne Mathematik an mir vorbeigegangen und ich habe einfach keine Lust, da wieder einzusteigen, weil es mir keine Freude bereiten wird. Soweit dieses Thema! Keine Ahnung, ob mir meine Gedanken kommen würden, wenn ich im Elfenbeinturm der Physik gefangen säße. So bin ich frei, wie ich freier nicht sein kann! Die ART ist jedenfalls nicht das A und O, da irrt auch Smolin, den ich selber schätze, weil er der Zeit den Raum gibt, der ihr gebührt. Und der geht über SRT und ART hinaus.
KirscheDie Vergangenheit ist über die Gegenwart verbrauchte Zukunft.
hast du, Otto, nicht vielleicht den einen Punkt getroffen, der sich auch zwischen den Gravitationsfeldern von Erde und Mond befinden wird? Es ist nicht ausgeschlossen, dass man diesen Punkt, und nur diesen einen und ebensolchen einen in anderen Fällen, als in Raumzeitgedanken einzig ausgestattet mit der Größe von jeweils Null in Zeit- und Raumeinheiten ansehen kann. Dort heben sich die Gravitationsfelder auf, es herrscht ein Gleichgewicht unter diesen weit wirkenden und von anderen Wirkungen befreiten Kräften und nur dort kann im Universum alles auf Null gesetzt sein.
Zumindest wäre dies meine einzige Idee, Ottos Feststellungen zu interpretieren.
Mathematik und Physik, gerade auch Differential- und Integralrechnung, waren einst meine Leidenschaften, Otto, die mir gründlich vergällt wurden, nachdem ich in meinem im Grunde nur altsprachlich ausgerichteten Gymnasium für Jungs vom eher schon dort verachteten neusprachlichen Zug auf den gerade neu eingerichteten naturwissenschaftlichen Zug wechselte, der sich dann aber mit nur 11 Personen aus 1-3 Jahre älteren Sitzenbleibern auch aus dem Mädchengymnasium meines Wohnortes rekrutierte. Ich habe es danach vorgezogen, mich studienmäßig anders zu orientieren und es nicht bereut. Denken an diese Zeit mag ich allerdings nicht und ebenso wenig erinnert. So sind fast 60 ohne Mathematik an mir vorbeigegangen und ich habe einfach keine Lust, da wieder einzusteigen, weil es mir keine Freude bereiten wird. Soweit dieses Thema! Keine Ahnung, ob mir meine Gedanken kommen würden, wenn ich im Elfenbeinturm der Physik gefangen säße. So bin ich frei, wie ich freier nicht sein kann! Die ART ist jedenfalls nicht das A und O, da irrt auch Smolin, den ich selber schätze, weil er der Zeit den Raum gibt, der ihr gebührt. Und der geht über SRT und ART hinaus.
Kirsche
Signatur:
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2345-127
03.06.2020 21:14
|
Hallo Kirsche,
Danke für die Hintergrund-Info.
Sicher wäre mein Interesse an Technik auch ganz anders verlaufen, wenn ich, wie Du, unter den von Dir geschilderten Umständen aufgewachsen wäre.
Das versäumte kann man leider nie wieder aufholen.
Mir fiel Mathe zum Glück immer leicht und die Gedankenakrobatik hat mir Spaß gemacht.
Ich hatte außerdem gute Lehrer. Einer meiner Professoren an der Uni kam aus dem Umfeld von Wernher von Braun.
Ich bin ihm bis heute für die ausgezeichnete Bildung und Lehre, die ich genossen habe, dankbar.
Gruß, Otto
Kirsche schrieb in Beitrag Nr. 2345-126:Mathematik und Physik, gerade auch Differential- und Integralrechnung, waren einst meine Leidenschaften, Otto, die mir gründlich vergällt wurden,
Danke für die Hintergrund-Info.
Sicher wäre mein Interesse an Technik auch ganz anders verlaufen, wenn ich, wie Du, unter den von Dir geschilderten Umständen aufgewachsen wäre.
Das versäumte kann man leider nie wieder aufholen.
Mir fiel Mathe zum Glück immer leicht und die Gedankenakrobatik hat mir Spaß gemacht.
Ich hatte außerdem gute Lehrer. Einer meiner Professoren an der Uni kam aus dem Umfeld von Wernher von Braun.
Ich bin ihm bis heute für die ausgezeichnete Bildung und Lehre, die ich genossen habe, dankbar.
Gruß, Otto
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2345-128
03.06.2020 21:32
|
Hallo Kirsche,
Genau diesen Gedanken bin ich nachgegangen und habe eine mögliche Analogie geprüft.
Cassinischen Kurven ähneln auf den ersten Blick den bekannten Potentiallinien zweier gravitativen Punktmassen.
Sie folgen aber unterschiedlichen Gesetzen.
Es geht um die Verknüpfung zwar zweier völlig gleicher mathematischen Terme, jedoch in einem Fall durch Addition, im anderen Fall durch Multiplikation.
Beide Gleichungen sind implizite Gleichungen, Typ F(x,y) = 0, auch Niveaulinien genannt.
Deshalb können Cassinischen Kurven als Potentiallinien interpretiert werden, ebenso deren Spiegelungen am Kreis.
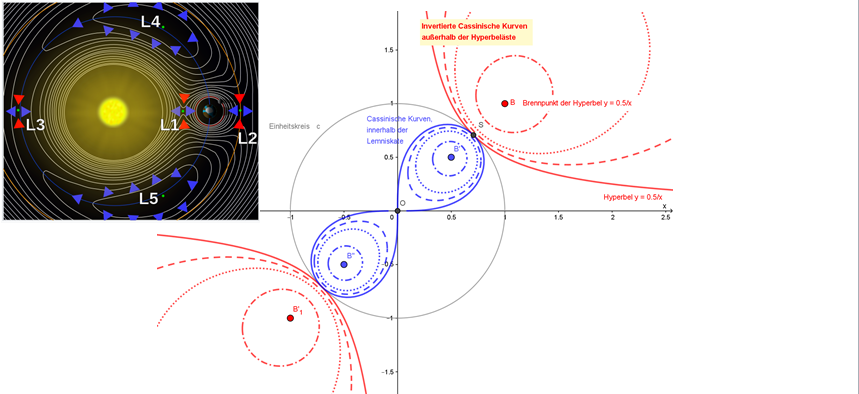
Bild: "Cassinische Kurven innerhalb der Lemniskate & ihre Inversionen"
- In Anlehnung an Gravitationspotentiale würden Cassinischen Kurven und ihrer Inversionen Massekonzentration in den Brennpunkten B, B', B'' und B'1 bedeuten.
- Die Änderungen der Raum- und der Zeitkomponente sind gleich.
- S (und seine Spiegelung) entsprächen den Lagrange-Punkten L1/L3.
- Auf dem Kreis c wäre eine Testmasse kräftefrei, labil in Richtung Achse B-B'.
- Punkt S auf dem Schwarzschildradius verliert die Eigenschaft "Lokalität".
Gruß, Otto
Kirsche schrieb in Beitrag Nr. 2345-126:hast du, Otto, nicht vielleicht den einen Punkt getroffen, der sich auch zwischen den Gravitationsfeldern von Erde und Mond befinden wird? Es ist nicht ausgeschlossen, dass man diesen Punkt, und nur diesen einen und ebensolchen einen in anderen Fällen, als in Raumzeitgedanken einzig ausgestattet mit der Größe von jeweils Null in Zeit- und Raumeinheiten ansehen kann. Dort heben sich die Gravitationsfelder auf, es herrscht ein Gleichgewicht unter diesen weit wirkenden und von anderen Wirkungen befreiten Kräften und nur dort kann im Universum alles auf Null gesetzt sein.
Genau diesen Gedanken bin ich nachgegangen und habe eine mögliche Analogie geprüft.
Cassinischen Kurven ähneln auf den ersten Blick den bekannten Potentiallinien zweier gravitativen Punktmassen.
Sie folgen aber unterschiedlichen Gesetzen.
Es geht um die Verknüpfung zwar zweier völlig gleicher mathematischen Terme, jedoch in einem Fall durch Addition, im anderen Fall durch Multiplikation.
Beide Gleichungen sind implizite Gleichungen, Typ F(x,y) = 0, auch Niveaulinien genannt.
Deshalb können Cassinischen Kurven als Potentiallinien interpretiert werden, ebenso deren Spiegelungen am Kreis.

Bild: "Cassinische Kurven innerhalb der Lemniskate & ihre Inversionen"
- In Anlehnung an Gravitationspotentiale würden Cassinischen Kurven und ihrer Inversionen Massekonzentration in den Brennpunkten B, B', B'' und B'1 bedeuten.
- Die Änderungen der Raum- und der Zeitkomponente sind gleich.
- S (und seine Spiegelung) entsprächen den Lagrange-Punkten L1/L3.
- Auf dem Kreis c wäre eine Testmasse kräftefrei, labil in Richtung Achse B-B'.
- Punkt S auf dem Schwarzschildradius verliert die Eigenschaft "Lokalität".
Gruß, Otto
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 2345-129
03.06.2020 21:56
|
Hallo Otto,
Jetzt erst, nachdem du das kleine Bild mit den Lagrange-Punkten eingebracht hast, verstehe ich, was du mit obiger Aussage meinst.
Das gilt sicher für die Langrange-Punkte zwischen zwei Massen mit Gravitationspotenzialen. Aber ich denke, für einen Punkt auf dem Schwarzschildradius (z.B. Punkt S) gilt das so nicht. Wie sollte ein Objekt in S sich bspw. in Richtung B bewegen können? Wo es doch dem Ereignishorizont nicht mehr in Richtung >1 entkommen kann.
Otto schrieb in Beitrag Nr. 2345-128:- Auf dem Kreis c wäre eine Testmasse kräftefrei, labil in Richtung Achse B-B'.
Jetzt erst, nachdem du das kleine Bild mit den Lagrange-Punkten eingebracht hast, verstehe ich, was du mit obiger Aussage meinst.
Das gilt sicher für die Langrange-Punkte zwischen zwei Massen mit Gravitationspotenzialen. Aber ich denke, für einen Punkt auf dem Schwarzschildradius (z.B. Punkt S) gilt das so nicht. Wie sollte ein Objekt in S sich bspw. in Richtung B bewegen können? Wo es doch dem Ereignishorizont nicht mehr in Richtung >1 entkommen kann.
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2345-130
03.06.2020 22:49
|
Hallo Claus,
Ich weiß es auch nicht.
Deshalb hatte ich das Wort "Anlehnung" markiert.
Für mich ist es ein offenes Problem.
Entweder ist die Analogie zu den Cassinischen Kurven ein Irrweg oder wir haben bisher ein völlig falsches Verständnis von SL.
Spannende Frage, finde ich.
Gruß, Otto
Claus schrieb in Beitrag Nr. 2345-129:Wie sollte ein Objekt in S sich bspw. in Richtung B bewegen können? Wo es doch dem Ereignishorizont nicht mehr in Richtung >1 entkommen kann.
Ich weiß es auch nicht.
Deshalb hatte ich das Wort "Anlehnung" markiert.
Für mich ist es ein offenes Problem.
Entweder ist die Analogie zu den Cassinischen Kurven ein Irrweg oder wir haben bisher ein völlig falsches Verständnis von SL.
Spannende Frage, finde ich.
Gruß, Otto
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2345-131
04.06.2020 03:50
|
Hallo Claus,
Die Cassinischen Kurven, die Hyperbelschar und der Einheitskreis (Schwarzschildradius) gelten nur für die Wirkung einer Punktmasse.
Masseanziehung spielt hier keine Rolle. Der Schwarzschildradius ist deshalb erst einmal kein Ereignishorizont.
Die Lagrange-Punkte im Gravitationsfeld sind dagegen das Resultat zweier Massen.
Analogien zwischen beiden Darstellungen sind deshalb mit Vorsicht zu betrachten und den Unterschied darf man nicht aus dem Auge verlieren.
Wichtig ist insbesondere, dass sowohl die Cassiischen Kurven als auch ihre Konversionen als Hyperbeln beides Potentialfelder darstellen!
Gruß, Otto
Noch eine wichtige Ergänzung:Claus schrieb in Beitrag Nr. 2345-129:Das gilt sicher für die Langrange-Punkte zwischen zwei Massen mit Gravitationspotenzialen.
Die Cassinischen Kurven, die Hyperbelschar und der Einheitskreis (Schwarzschildradius) gelten nur für die Wirkung einer Punktmasse.
Masseanziehung spielt hier keine Rolle. Der Schwarzschildradius ist deshalb erst einmal kein Ereignishorizont.
Die Lagrange-Punkte im Gravitationsfeld sind dagegen das Resultat zweier Massen.
Analogien zwischen beiden Darstellungen sind deshalb mit Vorsicht zu betrachten und den Unterschied darf man nicht aus dem Auge verlieren.
Wichtig ist insbesondere, dass sowohl die Cassiischen Kurven als auch ihre Konversionen als Hyperbeln beides Potentialfelder darstellen!
Gruß, Otto
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 2345-132
04.06.2020 05:37
|
Hallo Otto,
Ja. Hierin liegt ein wesentlicher Unterschied zwischen den Lagrange-Punkten und den "Schwerpunkten" der Cassinischen Kurven:
Bei den Cassinischen Kurven wird die Krümmung an diesen Punkten maximal. Die Kurve ist stets geschlossen.
In der Nähe der Lagrange-Punkte öffnet sich die Äquipotenzialkurve dagegen in Richtung zur zweiten Masse, denn die beiden Massen krümmen in entgegengesetzte Richtungen. Dadurch wird die (Gesamt)-Krümmung am Lagrange-Punkt null.
Eben dies macht im Falle Lagrange die Labilität des Punktes aus und das gilt m.E. nicht für die Wendepunkte/ Schwerpunkte der Cassini-Kurven.
Otto schrieb in Beitrag Nr. 2345-131:Die Lagrange-Punkte im Gravitationsfeld sind dagegen das Resultat zweier Massen.
Ja. Hierin liegt ein wesentlicher Unterschied zwischen den Lagrange-Punkten und den "Schwerpunkten" der Cassinischen Kurven:
Bei den Cassinischen Kurven wird die Krümmung an diesen Punkten maximal. Die Kurve ist stets geschlossen.
In der Nähe der Lagrange-Punkte öffnet sich die Äquipotenzialkurve dagegen in Richtung zur zweiten Masse, denn die beiden Massen krümmen in entgegengesetzte Richtungen. Dadurch wird die (Gesamt)-Krümmung am Lagrange-Punkt null.
Eben dies macht im Falle Lagrange die Labilität des Punktes aus und das gilt m.E. nicht für die Wendepunkte/ Schwerpunkte der Cassini-Kurven.
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2345-133
04.06.2020 07:45
|
Moin Claus,
auf die Schnelle:
Sie verhalten sich wie der Sattelpunkt einer Sattelfläche.
Die Rate der Krümmungen stehen senkrecht zueinander im umgekehrte Verhältnis.
Sie verhalten sich wie eine Oberfläche z² = x² - y² (oder um -45° gedreht die Komponenten y = 1/x) mit dem Raumanteil x und den Zeitanteil y.
Gruß, Otto
auf die Schnelle:
Die Lagrange-Punkte l1, L2. L3 und L4 sind in eine Richtung stabil (rot) und in die andere Richtung labil (blau).Claus schrieb in Beitrag Nr. 2345-132:In der Nähe der Lagrange-Punkte öffnet sich die Äquipotenzialkurve dagegen in Richtung zur zweiten Masse, denn die beiden Massen krümmen in entgegengesetzte Richtungen. Dadurch wird die (Gesamt)-Krümmung am Lagrange-Punkt null.
Sie verhalten sich wie der Sattelpunkt einer Sattelfläche.
Die Rate der Krümmungen stehen senkrecht zueinander im umgekehrte Verhältnis.
Sie verhalten sich wie eine Oberfläche z² = x² - y² (oder um -45° gedreht die Komponenten y = 1/x) mit dem Raumanteil x und den Zeitanteil y.
Gruß, Otto
[Gäste dürfen nur lesen]
| Beiträge: 905, Mitglied seit 7 Jahren |
Beitrag Nr. 2345-134
04.06.2020 16:52
|
Hallo Otto, (hallo Forum),
die von dir grafisch dargestellten Punkte nennen sich also Lagrange-Punkte. Als Beispiele dienten die Gravitationswirkungen von z.B. Erde und Mond, deren, ich drücke es bewusst so aus, unterschiedliche Massen durch die Rotationsbewegung des Mondes um die Sonne ausgeglichen werden. Ob die ART eine bessere Erklärung liefert, muss hier wahrscheinlich nicht geklärt werden und kann wohl für meine Fragen offen bleiben:
1. Obwohl dem Gefundenen also offenbar doch nicht wirklich etwas Neues zu Grunde liegt, lohnt es sich aus meiner Sicht, über die Grafik weiter nachzudenken, zumal sie in ihrer Mitte nicht einen sondern m.E. zwei dieser Lagrangepunkte aufweist bzw. einen, der je nach Vor- oder Rücklauf in deinen „Hasenohren“ an raumzeitlich unterschiedlichen Stellen auftaucht. Wie kannst du das erklären, Otto?
2. Zeigen 2 stabil auf Abstand gehaltene Wasserstoffatome ebenfalls einen stabilen Lagrangepunkt, auch dann, wenn sie nicht umeinander kreisen?
3. Jedenfalls müsste es solchen Punkt auch zwischen 2 Galaxien bzw. Gruppen von Galaxien geben, die sich voneinander entfernen. Dabei weist Gravitation ins Unendliche. Wahrscheinlich ist dieser Punkt dennoch lange keinerlei Veränderungen unterworfen, er bleibt dimensionslos, vergrößert sich also lange Zeit bis wohl zu dieser Unendlichkeit nicht. Was passiert aber, wenn die durch die Dunkle Energie oder was auch immer gesteuerte Ausdehnung des Raumes soweit fortgeschritten ist, dass die Gravitation an diesem Punkt den Wert von Null unterschreiten müsste? Würde das nicht zuvor schon bremsend wirken und die Unterschreitung verhindern müssen? Würde sich ggf. aber anders als sonst üblich, also ein negatives SL bilden?
4. Müsste eine derartige Bremswirkung nicht schon den Zusammenprall von 2 Wasserstoffatomen gleicher Gravitationswirkung verhindern, die übrigen Kräfte ohnehin vernachlässigend?
Die Frage, die ich mir stelle ist, also nicht die eines üblichen, positiven und deshalb ggf. verdampfenden SL, welches auch schon diverse Fragen offen lässt, sondern insbesondere die, was unter der Gravitation eines einzelnen Wasserstoffatoms zu verstehen ist. Gedanken dazu hatte ich hier in diesem Thread geäußert. Ferner die Frage, ob und inwieweit negative SL denkbar sind. Wenn positive SL verdampfen, müssten negative dann vielleicht doch aus dem Nichts anwachsen? Wenn so der Urknall zu erklären wäre, könnte ich mir wiederum Multiversen vorstellen, die aber nicht mit dem unseren verbunden sein könnten. (Ich bevorzuge weiter den Urprall).
KirscheDie Vergangenheit ist über die Gegenwart verbrauchte Zukunft.
die von dir grafisch dargestellten Punkte nennen sich also Lagrange-Punkte. Als Beispiele dienten die Gravitationswirkungen von z.B. Erde und Mond, deren, ich drücke es bewusst so aus, unterschiedliche Massen durch die Rotationsbewegung des Mondes um die Sonne ausgeglichen werden. Ob die ART eine bessere Erklärung liefert, muss hier wahrscheinlich nicht geklärt werden und kann wohl für meine Fragen offen bleiben:
1. Obwohl dem Gefundenen also offenbar doch nicht wirklich etwas Neues zu Grunde liegt, lohnt es sich aus meiner Sicht, über die Grafik weiter nachzudenken, zumal sie in ihrer Mitte nicht einen sondern m.E. zwei dieser Lagrangepunkte aufweist bzw. einen, der je nach Vor- oder Rücklauf in deinen „Hasenohren“ an raumzeitlich unterschiedlichen Stellen auftaucht. Wie kannst du das erklären, Otto?
2. Zeigen 2 stabil auf Abstand gehaltene Wasserstoffatome ebenfalls einen stabilen Lagrangepunkt, auch dann, wenn sie nicht umeinander kreisen?
3. Jedenfalls müsste es solchen Punkt auch zwischen 2 Galaxien bzw. Gruppen von Galaxien geben, die sich voneinander entfernen. Dabei weist Gravitation ins Unendliche. Wahrscheinlich ist dieser Punkt dennoch lange keinerlei Veränderungen unterworfen, er bleibt dimensionslos, vergrößert sich also lange Zeit bis wohl zu dieser Unendlichkeit nicht. Was passiert aber, wenn die durch die Dunkle Energie oder was auch immer gesteuerte Ausdehnung des Raumes soweit fortgeschritten ist, dass die Gravitation an diesem Punkt den Wert von Null unterschreiten müsste? Würde das nicht zuvor schon bremsend wirken und die Unterschreitung verhindern müssen? Würde sich ggf. aber anders als sonst üblich, also ein negatives SL bilden?
4. Müsste eine derartige Bremswirkung nicht schon den Zusammenprall von 2 Wasserstoffatomen gleicher Gravitationswirkung verhindern, die übrigen Kräfte ohnehin vernachlässigend?
Die Frage, die ich mir stelle ist, also nicht die eines üblichen, positiven und deshalb ggf. verdampfenden SL, welches auch schon diverse Fragen offen lässt, sondern insbesondere die, was unter der Gravitation eines einzelnen Wasserstoffatoms zu verstehen ist. Gedanken dazu hatte ich hier in diesem Thread geäußert. Ferner die Frage, ob und inwieweit negative SL denkbar sind. Wenn positive SL verdampfen, müssten negative dann vielleicht doch aus dem Nichts anwachsen? Wenn so der Urknall zu erklären wäre, könnte ich mir wiederum Multiversen vorstellen, die aber nicht mit dem unseren verbunden sein könnten. (Ich bevorzuge weiter den Urprall).
Kirsche
Signatur:
Beitrag zuletzt bearbeitet von Kirsche am 04.06.2020 um 16:56 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 1.644, Mitglied seit 16 Jahren |
Beitrag Nr. 2345-135
05.06.2020 08:43
|
Hallo Otto,
ohne die von Dir angestellten mathematischen Überlegungen zu verstehen fällt mir auf, dass mit dieser Formel auch ein Raumzeitintervall (Weltlinie)l in einem zweidimensionalen (räumlich eindimensionalen) Raumzeitkoordinatensystem berechnet wird:
Raumzeitintervall2=Zeitintervall2 -Raumintervall2
MfG
HartiWichtig ist, dass man nicht aufhört zu fragen. A.E.
Otto schrieb in Beitrag Nr. 2345-133:Sie verhalten sich wie eine Oberfläche z² = x² - y² (oder um -45° gedreht die Komponenten y = 1/x) mit dem Raumanteil x und den Zeitanteil y.
ohne die von Dir angestellten mathematischen Überlegungen zu verstehen fällt mir auf, dass mit dieser Formel auch ein Raumzeitintervall (Weltlinie)l in einem zweidimensionalen (räumlich eindimensionalen) Raumzeitkoordinatensystem berechnet wird:
Raumzeitintervall2=Zeitintervall2 -Raumintervall2
MfG
Harti
Signatur:
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 2345-136
05.06.2020 22:43
|
Hallo Otto und Harti,
Erinnere mich an eine Diskussion mit Bauhof (siehe Beitrag-Nr. 1164-33).
Ist es so, dass der Raum konvex, die Zeit dagegen konkav gekrümmt wird?
Otto schrieb in Beitrag Nr. 2345-133:Die Lagrange-Punkte l1, L2. L3 und L4 sind in eine Richtung stabil (rot) und in die andere Richtung labil (blau).
Sie verhalten sich wie der Sattelpunkt einer Sattelfläche.
Die Rate der Krümmungen stehen senkrecht zueinander im umgekehrte Verhältnis.
Sie verhalten sich wie eine Oberfläche z² = x² - y²
Harti schrieb in Beitrag Nr. 2345-135:... fällt mir auf, dass mit dieser Formel auch ein Raumzeitintervall (Weltlinie)l in einem zweidimensionalen (räumlich eindimensionalen) Raumzeitkoordinatensystem berechnet wird:
Raumzeitintervall2=Zeitintervall2 -Raumintervall2
Erinnere mich an eine Diskussion mit Bauhof (siehe Beitrag-Nr. 1164-33).
Ist es so, dass der Raum konvex, die Zeit dagegen konkav gekrümmt wird?
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2345-137
06.06.2020 01:32
|
Hallo Claus und Harti,
Die räumliche Darstellung von Oberflächen erleichtert das Verstehen von Funktionen (Potentiallinien) mit zwei Variablen.
Die Änderungsrate als Tangente an die Oberfläche (oder auch die Änderungsrate der Krümmung) lassen sich so gut veranschaulichen.
Die Hyperbel y = 1/x ist nach einfacher Umstellung gleichwertig mit x = 1/y.
Während die Änderungsrate x zunimmt, wird y kleiner - und umgekehrt.
Wenn (infolge Masse) die Änderung des Zeitanteils "dy" der Raumzeit "ds" konvex gekrümmt ist, ist die Änderung des Raumanteils "dx" konkav gekrümmt und umgekehrt.
Gruß, Otto
Genauso war mein Kommentar gemeint.Claus schrieb in Beitrag Nr. 2345-136:Ist es so, dass der Raum konvex, die Zeit dagegen konkav gekrümmt wird?
Die räumliche Darstellung von Oberflächen erleichtert das Verstehen von Funktionen (Potentiallinien) mit zwei Variablen.
Die Änderungsrate als Tangente an die Oberfläche (oder auch die Änderungsrate der Krümmung) lassen sich so gut veranschaulichen.
Die Hyperbel y = 1/x ist nach einfacher Umstellung gleichwertig mit x = 1/y.
Während die Änderungsrate x zunimmt, wird y kleiner - und umgekehrt.
Wenn (infolge Masse) die Änderung des Zeitanteils "dy" der Raumzeit "ds" konvex gekrümmt ist, ist die Änderung des Raumanteils "dx" konkav gekrümmt und umgekehrt.
Gruß, Otto
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2345-138
06.06.2020 01:57
|
Hallo Kirsche,
Meines Erachtens lassen sich so dynamische Veränderungen der Raumzeit darstellen, die wir als Schwingungen kennen.
Ich habe dafür eine dynamische Graphik vorbereitet und Manu gebeten, diese im Forum hochlauten zu dürfen.
Manu hat im Moment jedoch ganz andere Probleme mit dem Umzug des Forums auf einen anderen Surver.
Das ist einer der Punkte, über die man dann nachdenken muß.
Wenn es um die Wirkung nicht nur einer Einzelmasse, sondern die Überlagerung mehrere Massen (wie auch bei Galaxien) geht, wird es mathematische sehr schwierig.
Eine mögliche Lösung vermute ich im Baryzentrum des Zweikörperproblems.
Gruß, Otto
Ich erfinde nichts Neues, sondern stelle nur die prinzipiellen Wirkungen von Masse nach der ART, graphisch dar.Kirsche schrieb in Beitrag Nr. 2345-134:Ob die ART eine bessere Erklärung liefert, muss hier wahrscheinlich nicht geklärt werden und kann wohl für meine Fragen offen bleiben:
... Obwohl dem Gefundenen also offenbar doch nicht wirklich etwas Neues zu Grunde liegt,
Darauf möchte ich später genauer eingehen.Kirsche schrieb in Beitrag Nr. 2345-134:zumal sie in ihrer Mitte nicht einen sondern m.E. zwei dieser Lagrangepunkte aufweist bzw. einen, der je nach Vor- oder Rücklauf in deinen „Hasenohren“ an raumzeitlich unterschiedlichen Stellen auftaucht. Wie kannst du das erklären, Otto?
Meines Erachtens lassen sich so dynamische Veränderungen der Raumzeit darstellen, die wir als Schwingungen kennen.
Ich habe dafür eine dynamische Graphik vorbereitet und Manu gebeten, diese im Forum hochlauten zu dürfen.
Manu hat im Moment jedoch ganz andere Probleme mit dem Umzug des Forums auf einen anderen Surver.
Möglich, aber ich vermute nicht.Kirsche schrieb in Beitrag Nr. 2345-134:Zeigen 2 stabil auf Abstand gehaltene Wasserstoffatome ebenfalls einen stabilen Lagrangepunkt, auch dann, wenn sie nicht umeinander kreisen?
Das ist einer der Punkte, über die man dann nachdenken muß.
Wenn es um die Wirkung nicht nur einer Einzelmasse, sondern die Überlagerung mehrere Massen (wie auch bei Galaxien) geht, wird es mathematische sehr schwierig.
Eine mögliche Lösung vermute ich im Baryzentrum des Zweikörperproblems.
Gruß, Otto
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2345-139
06.06.2020 02:17
|
Hallo Claus,
- Die Änderungsrate ist nicht zu verwechseln mit dem Wert/Betrag des Zustandes.
Der Betrag des Zustandes erreicht dort ein Maximum (wie zum Beispiel der Kurve sin(+-90°)) wo die Änderungsrate (sin'() = cos()) Null ist.
Gruß, Otto
- Die Brennpunkte der Cassinsichen Kurven und der Hyperbelschar sind Extremata eines Potentialfeldes. Sie ließen sich als Ursache von Masse erklären.Claus schrieb in Beitrag Nr. 2345-132:Eben dies macht im Falle Lagrange die Labilität des Punktes aus und das gilt m.E. nicht für die Wendepunkte/ Schwerpunkte der Cassini-Kurven.
- Die Änderungsrate ist nicht zu verwechseln mit dem Wert/Betrag des Zustandes.
Der Betrag des Zustandes erreicht dort ein Maximum (wie zum Beispiel der Kurve sin(+-90°)) wo die Änderungsrate (sin'() = cos()) Null ist.
Gruß, Otto
Beitrag zuletzt bearbeitet von Otto am 06.06.2020 um 02:18 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 1.246, Mitglied seit 10 Jahren |
Beitrag Nr. 2345-140
11.06.2020 06:22
|
Hallo, alle zusammen,
Für weitere Einzelheiten zu den Ähnlichkeiten der Potentiallinien zweier Massen mit den sogenannten Cassinische Kurven siehe neu eröffneter Thread, Beitrag Nr. 2347-2.
Otto
Für weitere Einzelheiten zu den Ähnlichkeiten der Potentiallinien zweier Massen mit den sogenannten Cassinische Kurven siehe neu eröffneter Thread, Beitrag Nr. 2347-2.
Otto
[Gäste dürfen nur lesen]
In diesem Forum dürfen nur Mitglieder schreiben. Hier kannst du dich anmelden



 Nach oben
Nach oben