Unendlichkeit in der Mathematik
Thema erstellt von Okotombrok
| Beiträge: 1.375, Mitglied seit 16 Jahren |
Beitrag Nr. 2045-44
19.06.2013 16:12
|
Irena schrieb in Beitrag Nr. 2045-41:Sie (die Zahl) ist aber unendlich, oder?! Wie dann bezeichnet man eine Zahl, die nach Komma in Unendlichkeit geht?Irena schrieb in Beitrag Nr. 2045-38:Ist nicht eine unendliche Zahl (Wurzel aus 2) kleiner als unendliche Zahl Pi?
Hallo Irena,
nein, die Zahl selbst ist nicht unendlich! Nur die Anzahl der Stellen hinter dem Komma ist unendlich groß. Nicht nur die Wurzel aus 2, sondern auch z.B. der Bruch 1/3 hat unendlich viele Dezimalstellen hinter dem Komma.
Nur weil 1/3 unendlich viele Dezimalstellen hinter dem Komma hat, ist deswegen diese Zahl nicht unendlich groß.
M.f.G. Eugen Bauhof
Signatur:
der Normale aus seinen Erfahrungen,
und der Dumme weiß alles besser.
Sokrates.
[Gäste dürfen nur lesen]
| Beiträge: 1.375, Mitglied seit 16 Jahren |
Beitrag Nr. 2045-45
19.06.2013 16:23
|
Irena schrieb in Beitrag Nr. 2045-38:Wenn man über Mengen spricht, dann eine Ungleichheit der Unendlichen Mengen ist anschaulich durch Vergleich der unendliche Menge der rationalen Zahlen und unendliche Menge der irrationalen Zahlen, die kleiner als die erste ist.
Hallo Irena,
leider falsch.
Die rationalen Zahlen lassen sich als Brüche von ganzen Zahlen darstellen. Zum Beispiel ist der Bruch 1/3 eine rationale Zahl.
Die irrationalen Zahlen lassen sich nicht als Brüche von ganzen Zahlen darstellen. Zum Beispiel ist die Wurzel aus 2 eine irrationale Zahl.
Die Menge der irrationalen Zahlen ist mächtiger als die Menge der rationalen Zahlen. Überlege mal, warum das so ist.
M.f.G. Eugen Bauhof
Signatur:
der Normale aus seinen Erfahrungen,
und der Dumme weiß alles besser.
Sokrates.
Beitrag zuletzt bearbeitet von Bauhof am 19.06.2013 um 16:24 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 1.503, Mitglied seit 17 Jahren |
Beitrag Nr. 2045-46
19.06.2013 18:36
|
ja, Eugen, mein Denkfehler.
Auch Beispiel, wie man mit einer Überzeugung ein Text verkehr liest. Da ich mit Irrationalen Zahlen die Pi-Zahl, Qudrat aus 2, Goldene Schnitt verbinde, dann schien mir sie seltener zu sein. Ich habe sogar Satz in meinem Buch über Mathematik verkehrt gelesen, nämlich auf der Stelle der irrationalen Menge habe ich rationale vorgestellt. Klassische Beispiel der Täuschung durch Voranstellung.
Also kann man irrationale Zahl ein Bruch nicht ganzzahlige Zahlen sehen? Wobei 4,3 teilen durch 2,15 ergibt schöne Zahl 2, die keine irrationale Zahl ist.
Auch Beispiel, wie man mit einer Überzeugung ein Text verkehr liest. Da ich mit Irrationalen Zahlen die Pi-Zahl, Qudrat aus 2, Goldene Schnitt verbinde, dann schien mir sie seltener zu sein. Ich habe sogar Satz in meinem Buch über Mathematik verkehrt gelesen, nämlich auf der Stelle der irrationalen Menge habe ich rationale vorgestellt. Klassische Beispiel der Täuschung durch Voranstellung.
Also kann man irrationale Zahl ein Bruch nicht ganzzahlige Zahlen sehen? Wobei 4,3 teilen durch 2,15 ergibt schöne Zahl 2, die keine irrationale Zahl ist.
[Gäste dürfen nur lesen]
| Beiträge: 1.375, Mitglied seit 16 Jahren |
Beitrag Nr. 2045-47
20.06.2013 10:44
|
Irena schrieb in Beitrag Nr. 2045-46:Also kann man irrationale Zahl ein Bruch nicht ganzzahlige Zahlen sehen?
Hallo Irena,
ich übersetze deine Frage in eine verständlichere Form:
Zitat:Also kann man eine irrationale Zahl nicht als einen Bruch mit zwei ganzen Zahlen sehen?
So ist es, ein Bruch mit einer ganzen Zahl im Zähler und einer ganzen Zahl im Nenner ist immer eine rationale Zahl und keine irrationale Zahl.
Irena schrieb in Beitrag Nr. 2045-46:Wobei 4,3 teilen durch 2,15 ergibt schöne Zahl 2, die keine irrationale Zahl ist.
Was willst du damit zum Ausdruck bringen?
Man kann alle Brüche, deren Zähler oder Nenner Dezimalzahlen sind, durch Erweitern auf die Form N/K bringen, wobei N und K ganze Zahlen sind. Dein Beispiel:
4,3/2,15 = (4,3•1000)/1000 / (2,15•1000)/1000
4,3/2,15 = (4300)/1000 / (2150)/1000
4,3/2,15 = 4300 / 2150 = 2
Oder ganz allgemein: Nicht nur der Quotient zweier ganzer Zahlen ist eine rationale Zahl, sondern auch der der Quotient zweier rationaler Zahlen ist eine rationale Zahl.
M.f.G. Eugen Bauhof
Signatur:
der Normale aus seinen Erfahrungen,
und der Dumme weiß alles besser.
Sokrates.
[Gäste dürfen nur lesen]
| Beiträge: 1.732, Mitglied seit 16 Jahren |
Beitrag Nr. 2045-48
25.06.2013 22:56
|
Bauhof schrieb in Beitrag Nr. 2045-47:Man kann alle Brüche, deren Zähler oder Nenner Dezimalzahlen sind, durch Erweitern auf die Form N/K bringen, wobei N und K ganze Zahlen sind.
Dezimalentwicklungen müssen nicht abbrechen. http://de.wikipedia.org/wiki/Dezimalsystem#Definition
Gemeint sind wohl Zähler und Nenner mit abbrechender Dezimalentwicklung wie im Beisipiel.
Zitat:4,3/2,15 = (4,3•1000)/1000 / (2,15•1000)/1000
...
Signatur:
Beitrag zuletzt bearbeitet von Thomas der Große am 25.06.2013 um 22:57 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 2.998, Mitglied seit 15 Jahren |
Beitrag Nr. 2045-49
26.06.2013 09:17
|
Zitat:4,3/2,15 = (4,3•1000)/1000 / (2,15•1000)/1000
...
es reicht aus, wenn Du Zähler und Nenner mit der gleichen Zahl multiplizierst:
4,3/2,15 = (4,3•1000)
entspricht 4300/2150
Die Division durch 1000 ausserhalb der Klammer kannst Du Dir sparen.
Signatur:

Der Erfahrene erkennt, dass er nicht alle Probleme lösen kann:smiley3:

Beitrag zuletzt bearbeitet von Hans-m am 26.06.2013 um 09:19 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 1.375, Mitglied seit 16 Jahren |
Beitrag Nr. 2045-50
26.06.2013 10:01
|
Hans-m schrieb in Beitrag Nr. 2045-49:Zitat:4,3/2,15 = (4,3•1000)/1000 / (2,15•1000)/1000
...
es reicht aus, wenn Du Zähler und Nenner mit der gleichen Zahl multiplizierst:
4,3/2,15 = (4,3•1000)/1000/ (2,15•1000)/1000
entspricht 4300/2150
Die Division durch 1000 ausserhalb der Klammer kannst Du Dir sparen.
Hallo Hans-m,
richtig, scharf beobachtet!
M.f.G. Eugen Bauhof
Signatur:
der Normale aus seinen Erfahrungen,
und der Dumme weiß alles besser.
Sokrates.
[Gäste dürfen nur lesen]
| Beiträge: 1.375, Mitglied seit 16 Jahren |
Beitrag Nr. 2045-51
26.06.2013 10:18
|
Thomas der Große schrieb in Beitrag Nr. 2045-48:Bauhof schrieb in Beitrag Nr. 2045-47:Man kann alle Brüche, deren Zähler oder Nenner Dezimalzahlen sind, durch Erweitern auf die Form N/K bringen, wobei N und K ganze Zahlen sind.
Dezimalentwicklungen müssen nicht abbrechen. http://de.wikipedia.org/wiki/Dezimalsystem#Definition
Gemeint sind wohl Zähler und Nenner mit abbrechender Dezimalentwicklung wie im Beisipiel.
Zitat:4,3/2,15 = (4,3•1000)/1000 / (2,15•1000)/1000
...
Hallo Thomas,
das weiß ich natürlich.
Nachdem ich bemerkte, dass Irena auf diesem Gebiet nicht so bewandert ist, wollte ich erst mal abwarten, ob sie das bisherige verstanden hat. Bei einer diesbezüglichen Nachfrage von Irena wäre ich auf das Thema “nichtabbrechende Dezimalentwicklungen“ eingegangen.
Ich vermeide es im Gegensatz zu Grtgrt, andere mit zusätzlichem Wissen zu überhäufen, wenn ich nicht sicher bin, dass das der Diskussionspartner auch verarbeiten kann. Was der Diskussionspartner verarbeiten kann, stellt sich erst nach weiterer Diskussion heraus.
Betrachte aber bitte dies jetzt nicht als eine Kritik an deinem Beitrag.
M.f.G. Eugen Bauhof
Signatur:
der Normale aus seinen Erfahrungen,
und der Dumme weiß alles besser.
Sokrates.
[Gäste dürfen nur lesen]
| Beiträge: 84, Mitglied seit 10 Jahren |
Beitrag Nr. 2045-52
01.07.2013 05:38
|
Die mathematische Unendlichkeit ist immer nur in eine Richtung unendlich.
Beispiel:
0,9 Periode 9
Die Unendlichkeit, also die Periode, setzt in diesem Fall unmittelbar mit der ersten Nachkommastelle ein.
Vor dem Komma kann dieser Wert nicht unendlich sein, sonst würde schliesslich niemals ein Komma folgen können.
Zudem gibt es unmögliche Perioden.
1 - 0,9 Periode 9 ergibt eine Unendlichkeit, bei der die 1 erst nach unendlich vielen 0 folgen kann.
0,1 Periode 1 ist keine kleinere Unendlichkeit im Verhältnis zum Wert 0,9 Periode 9.
Unendlichkeiten können nicht größer oder kleiner sein.
Unendlichkeiten unterscheiden sich qualitativ, nicht quantitativ.
Zwischen 0 und 1 gibt es unendlich viele Zahlen mit Nachkommastellen.
Innerhalb der unendlich vielen Zahlen mit Nachkommastellen gibt es unendlich viele Zahlen, die eine Periode sein können.
Zwischen den endlichen Zahlen 0 und 1 liegen unendlich viele Zahlen, von denen wiederum unendlich viele Zahlen Perioden sein können.
Rein theoretisch gibt es die Zahl 1 nicht.
Denn schon nach einer einzigen Unendlichkeit kann keine zweite Unendlichkeit folgen.
Mathematik ist in sich ein Paradoxon.
Unendlich ist kein mathematischer Wert.
Wäre er einer, so ergebe unendlich - 1 einen Wert kleiner unendlich.
Man kann sich der Unendlichkeit auch nicht annähern, es kann nichts gegen unendlich tendieren.
Könnte ich unendlich lange leben, so wäre ich an meinem 40. Geburtstag genauso weit von meinem Tod entfernt wie an meinem 1.000.000.000. Geburtstag.
Unendlichkeit ist kein Endpunkt.Man kann sich etwas nicht Vorhandenem nicht annähern.Es ist sozusagen ein Weg ohne Ziel.
Mein zunehmendes Alter würde also nur gegen meinen nächsten Geburtstag tendieren.Und das unendlich oft.
2 x 0,9 Periode 9 ergibt 1,9 Periode 9.
Eigentlich müsste nach der unendlichen 9 noch eine 8 folgen, aber ich will nicht kleinlich sein.
In der Mathematik lassen sich Unendlichkeiten vervielfachen oder sogar teilen.
Das ist nur mathematisch möglich.
Wenn ich unendlich lange leben könnte, könnte ich zu keinem Zeitpunkt sagen, daß jetzt die Hälfte meiner Lebenszeit vorbei wäre.
Meine Lebenszeit liesse sich nicht halbieren.
Sie liesse sich auch nicht durch Multiplikation oder Addition verlängern.
Ich könnte z.B. nicht zwei Mal unendlich lange leben.
Es gibt einen großen Unterschied zwischen mathematischer und physikalischer Unendlichkeit.Sie sind unterschiedlicher Natur.
Die Eigenschaften der mathematischen Unendlichkeit sind physikalischer Nonsens.
Wenn die Kreiszahl pi tatsächlich unendlich ist, so wird man unendlich lange brauchen, um diese Zahl darstellen zu können.
Und das, obwohl der zugrunde liegende Kreis in seiner Ausdehnung niemals unendlich ist.
Ein endlicher Kreis beruht auf einer unendlichen Konstante.
Die endliche Unendlichkeit - ein Paradoxon der Mathematik.Wahrheit ist frei von Vermutung.
Theorie ist immer eine formulierte Vermutung.
Beispiel:
0,9 Periode 9
Die Unendlichkeit, also die Periode, setzt in diesem Fall unmittelbar mit der ersten Nachkommastelle ein.
Vor dem Komma kann dieser Wert nicht unendlich sein, sonst würde schliesslich niemals ein Komma folgen können.
Zudem gibt es unmögliche Perioden.
1 - 0,9 Periode 9 ergibt eine Unendlichkeit, bei der die 1 erst nach unendlich vielen 0 folgen kann.
0,1 Periode 1 ist keine kleinere Unendlichkeit im Verhältnis zum Wert 0,9 Periode 9.
Unendlichkeiten können nicht größer oder kleiner sein.
Unendlichkeiten unterscheiden sich qualitativ, nicht quantitativ.
Zwischen 0 und 1 gibt es unendlich viele Zahlen mit Nachkommastellen.
Innerhalb der unendlich vielen Zahlen mit Nachkommastellen gibt es unendlich viele Zahlen, die eine Periode sein können.
Zwischen den endlichen Zahlen 0 und 1 liegen unendlich viele Zahlen, von denen wiederum unendlich viele Zahlen Perioden sein können.
Rein theoretisch gibt es die Zahl 1 nicht.
Denn schon nach einer einzigen Unendlichkeit kann keine zweite Unendlichkeit folgen.
Mathematik ist in sich ein Paradoxon.
Unendlich ist kein mathematischer Wert.
Wäre er einer, so ergebe unendlich - 1 einen Wert kleiner unendlich.
Man kann sich der Unendlichkeit auch nicht annähern, es kann nichts gegen unendlich tendieren.
Könnte ich unendlich lange leben, so wäre ich an meinem 40. Geburtstag genauso weit von meinem Tod entfernt wie an meinem 1.000.000.000. Geburtstag.
Unendlichkeit ist kein Endpunkt.Man kann sich etwas nicht Vorhandenem nicht annähern.Es ist sozusagen ein Weg ohne Ziel.
Mein zunehmendes Alter würde also nur gegen meinen nächsten Geburtstag tendieren.Und das unendlich oft.
2 x 0,9 Periode 9 ergibt 1,9 Periode 9.
Eigentlich müsste nach der unendlichen 9 noch eine 8 folgen, aber ich will nicht kleinlich sein.
In der Mathematik lassen sich Unendlichkeiten vervielfachen oder sogar teilen.
Das ist nur mathematisch möglich.
Wenn ich unendlich lange leben könnte, könnte ich zu keinem Zeitpunkt sagen, daß jetzt die Hälfte meiner Lebenszeit vorbei wäre.
Meine Lebenszeit liesse sich nicht halbieren.
Sie liesse sich auch nicht durch Multiplikation oder Addition verlängern.
Ich könnte z.B. nicht zwei Mal unendlich lange leben.
Es gibt einen großen Unterschied zwischen mathematischer und physikalischer Unendlichkeit.Sie sind unterschiedlicher Natur.
Die Eigenschaften der mathematischen Unendlichkeit sind physikalischer Nonsens.
Wenn die Kreiszahl pi tatsächlich unendlich ist, so wird man unendlich lange brauchen, um diese Zahl darstellen zu können.
Und das, obwohl der zugrunde liegende Kreis in seiner Ausdehnung niemals unendlich ist.
Ein endlicher Kreis beruht auf einer unendlichen Konstante.
Die endliche Unendlichkeit - ein Paradoxon der Mathematik.
Signatur:
Theorie ist immer eine formulierte Vermutung.
[Gäste dürfen nur lesen]
| Beiträge: 1.732, Mitglied seit 16 Jahren |
Beitrag Nr. 2045-53
02.07.2013 22:21
|
Jense schrieb in Beitrag Nr. 2045-52:1 - 0,9 Periode 9 ergibt eine Unendlichkeit, bei der die 1 erst nach unendlich vielen 0 folgen kann.
Hallo Jense,
wenn Du die Begriffe "unendliche Dezimalentwicklung" und "unendlich große Zahlen" unterscheidest,
dann kann ich Deinen Beitrag nachvollziehen und komme jeweils zu dem gleichen Ergebnis.
Z.B. die Kreiszahl pi hat eine unendliche Dezimalentwicklung, ist aber nicht viel größer als die Zahl 3.
Bei "0,9 Periode 9" stelt man sich eine Folge von Zahlen vor
0.9, 0.99, 0.999, 0.9999, 0.99999, usw.,
die immer näher an die 1 kommt und das ist etwas anderes als die konstante Folge
1, 1, 1, 1, 1, usw.
Bei Deiner Rechnung "1- 0,9 Periode 9" siehst Du also eine Folge von Differenzen
0.1, 0.01, 0.0001, 0.00001, ....
die gegen Null geht.
Genau nach dem Muster wird Gleichheit von reellen Zahlen definiert:
Zwei Folgen haben den gleichen Grenzwert, wenn ihre Differenz eine Nullfolge ist.
Für die Folgen zu 0,9 Periode 9 und 1 heißt das, dass die Grenzwerte tatsächlich die gleichen reellen Zahlen sind.
Hier meinst Du vermutlich die Eigenschaft, "unendlich - 1 = unendlich",Zitat:Unendlichkeiten unterscheiden sich qualitativ, nicht quantitativ.
wobei man dazu sagen müßte, wie das definiert sein soll und was da gerechnet wird.
Angenommen, wir spielen die Reise nach Jerusalem mit unendlich vielen Personen
"unendlich viele Personen" soll heißen, soviele wie es natürliche Zahlen gibt.
Zuerst sitzt jede der Personen (p1, p2, p3, ...) auf genau einem der Stühle (s1, s2, s3, ....) und zwar mit der Zuordnung
(p1 --> s1, p2--> s2, p3 --> s3, p4-->s4, ...)
Dann wird ein Stuhl entfernt, z.B. s1, und in der nächsten Runde kriegt jeder wieder einen Sitzplatz, z.B.
(p1 --> s2, p2--> s3, p3 --> s4, p4-->s5, p5 --> p6, ...)
Die Zahl der Elemente der Menge der natürlichen Zahlen wird aleph0 bezeichnet.
Am Anfang haben wir aleph0 Personen und aleph0 Stühle.
In der nächsten Runde haben wir aleph0 Personen und aleph0-1 Stühle.
Weil jeder Person eindeutig ein Stuhl zugeordnet ist, kann man schliessen
aleph0-1 = aleph0.
Dann machst Du noch Aussagen der "Es gibt unendlich viele periodische Zahlen ...".
Man kann, glaub ich zeigen, dass die periodischen Zahlen genau die rationalen Zahlen sind,
also die, die man als Brüche von ganzen Zahlen z/n schreiben kann.
lg
Thomas
Signatur:
Beitrag zuletzt bearbeitet von Thomas der Große am 03.07.2013 um 20:30 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 1.732, Mitglied seit 16 Jahren |
Beitrag Nr. 2045-54
02.07.2013 22:32
|
Hallo Bauhof,
bisher ist alles gerade.
Eine interessante Frage, die Du oben gestellt hattest, war die zur Kardinalität der sog. "ALLE"-Menge.
Um eine Antwort zu finden, muss man dir richtigen Begriffe wählen, bzw. erweitern.
Die Gesamtheit der Mengen ist keine Menge, wie Du oben festgestellt hast.
In der Mathematik hat man für "Gesamtheit von Objekten mit spezifischen Eigenschaften"
den allgemeineren Begriff Klasse eingeführt.
http://de.wikipedia.org/wiki/Klasse_(Mengenlehre)
Und so spricht man wohldefiniert von der Klasse der Mengen.
Die kürze ich ab jetzt ab mit KM.
Deine Frage ist dann die, ob man KM eine Kardinalität zuordnen kann.
Aus dem Wikipedia-Artikel zur Kardinalzahl
http://de.wikipedia.org/wiki/Kardinalzahl_(Mathematik)
benötige ich 2 Aussage:
(A) Die Gleichmächtigkeit von Mengen ist eine Äquivalenzrelation auf der Klasse aller Mengen.
(B) Man kann ... die Mächtigkeit von Mengen untersuchen, ohne Kardinalzahlen überhaupt zu benutzen.
Mit diesen will ich die Begriff Kardinalität für die Klasse der Mengen zu definieren.
Zum Begriff Kardinalität:
Den Begriff Kardinalität kann man sich für endliche Menge mit "Anzahl der Elemente" vorstellen.
[1] |{1, 4, 6, 20, 24}| = |{345, 2, -1, 33, 11}| = 5
Für allgemeine unendliche Mengen ist es ziemlich schwer, Zahlen zu konstruieren, die eine Anzahl von Elementen
so einer Menge repräsentieren könnte. Schon die nicht-axiomatische Konstruktion der rellen Zahlen mit
unendlichen Reihen ist ein gewaltiger algebraischer Klimmzug. Deswegen versucht man das gar nicht erst,
sondern betrachtet Klassen von Mengen gleicher Mächtigkeit und nennt jede solche Klasse Kardinalzahl.
Definition 1
Zu jeder Menge M sei |M| die Klasse der zu M gleichächtigen Mengen.
card(M):=|M| heiße Kardinalzahl von M.
Die Klasse der Mengen mit 5 Elementen
[2] |{1, 4, 6, 20, 24}| = |{345, 2, -1, 33, 11}| =: K5
ist also keine natürliche Zahl. Aber man kann die Klassen mit endlicher Elementeanzahl eindeutig zuordnen mit
S: n <-> Kn für n€IN0
[1'] |{1, 4, 6, 20, 24}| = |{345, 2, -1, 33, 11}| = K5 = S(5)
Erst mit dieser Identifizierung S kann man Gleichungen [1] oben mit "=5" schreiben.
Die Kardintlität war oben nur für Mengen defininert.
Man kann diese Definition wohldefininert auf die Kardinalität selbst fortsetzen
Definition 2
Zu jeder Menge M sei |M| die Klasse der zu M gleichächtigen Mengen.
card(|M|):=|M| heiße Kardinalzahl von |M|.
Der wesentlich Unterschied zu Definition 1 ist der, dass wir nicht eine Menge zuordnen,
sondern eine Klasse.
Wohldefininertheit in Definition 2:
Für jede Menge M' aus Klasse |M| ist card(M') = |M'| = |M|
Damit ist die Zuordnung M' -> card(M') konstant auf |M|
und deswegen card(|M|):=|M| wohldefininert.
Definition 3
Sei K eine Unterklasse von KM, die aus Kardinalzahlen besteht.
1. Es sei
card(K) := K
2. Für jede Menge M sei card(|M|)<=card(K) genau dann,
wenn es eine Obermenge M'>=M gibt, die zur Klasse K gehört.
Wohldefininertheit in Definition 3:
zu 1.) Da Gleichmächtigkeit eine Äquivalentrelation in KM ist,
zerfällt KM genauso wie die Unterklasse K in wohlunterschiedene Äquivalenzklassen, bzw. Kardinalzahlen.
Mit Definition 2 wird jeder zu K gehörigen Kardinalzahl eindeutig sie selbst zugeordnet.
card(K) ist gerade die Gesamheit dieser Kardinalzahlen-weisen Zuordnungen.
zu 2.) Hier muss man die Verträglichkeit mit der Halbordnung der Kardinalzahlen zeigen
und wesentlich die Transitivität der "<="-Relation. Das mach ich jetzt nicht, weil
mehr fieselig als schwer.
Resultat:
Aus Definition 3, 1.) folgt card(KM) = KM
Aus Definition 3, 2.) folgt für jede Menge M ist card(M) = card(|M|) < card(KM),
denn card(|M|) = card(M) < card(P(M)) <= card(KM).
Dabei ist die letzte Ungleichheit "<" eine Aussage von Georg Cantor
http://de.wikipedia.org/wiki/Satz_von_CantorIch bin begeistert!
Bauhof schrieb in Beitrag Nr. 2045-51:Betrachte aber bitte dies jetzt nicht als eine Kritik an deinem Beitrag.
bisher ist alles gerade.
Bauhof schrieb in Beitrag Nr. 2042-34:
Ich fasse alle unendlich großen Mengen zu einer neuen Menge zusammen und nenne diese neue Menge ALLE. Welche Mächtigkeit hat die Menge ALLE?
Eine interessante Frage, die Du oben gestellt hattest, war die zur Kardinalität der sog. "ALLE"-Menge.
Um eine Antwort zu finden, muss man dir richtigen Begriffe wählen, bzw. erweitern.
Die Gesamtheit der Mengen ist keine Menge, wie Du oben festgestellt hast.
In der Mathematik hat man für "Gesamtheit von Objekten mit spezifischen Eigenschaften"
den allgemeineren Begriff Klasse eingeführt.
http://de.wikipedia.org/wiki/Klasse_(Mengenlehre)
Und so spricht man wohldefiniert von der Klasse der Mengen.
Die kürze ich ab jetzt ab mit KM.
Deine Frage ist dann die, ob man KM eine Kardinalität zuordnen kann.
Aus dem Wikipedia-Artikel zur Kardinalzahl
http://de.wikipedia.org/wiki/Kardinalzahl_(Mathematik)
benötige ich 2 Aussage:
(A) Die Gleichmächtigkeit von Mengen ist eine Äquivalenzrelation auf der Klasse aller Mengen.
(B) Man kann ... die Mächtigkeit von Mengen untersuchen, ohne Kardinalzahlen überhaupt zu benutzen.
Mit diesen will ich die Begriff Kardinalität für die Klasse der Mengen zu definieren.
Zum Begriff Kardinalität:
Den Begriff Kardinalität kann man sich für endliche Menge mit "Anzahl der Elemente" vorstellen.
[1] |{1, 4, 6, 20, 24}| = |{345, 2, -1, 33, 11}| = 5
Für allgemeine unendliche Mengen ist es ziemlich schwer, Zahlen zu konstruieren, die eine Anzahl von Elementen
so einer Menge repräsentieren könnte. Schon die nicht-axiomatische Konstruktion der rellen Zahlen mit
unendlichen Reihen ist ein gewaltiger algebraischer Klimmzug. Deswegen versucht man das gar nicht erst,
sondern betrachtet Klassen von Mengen gleicher Mächtigkeit und nennt jede solche Klasse Kardinalzahl.
Definition 1
Zu jeder Menge M sei |M| die Klasse der zu M gleichächtigen Mengen.
card(M):=|M| heiße Kardinalzahl von M.
Die Klasse der Mengen mit 5 Elementen
[2] |{1, 4, 6, 20, 24}| = |{345, 2, -1, 33, 11}| =: K5
ist also keine natürliche Zahl. Aber man kann die Klassen mit endlicher Elementeanzahl eindeutig zuordnen mit
S: n <-> Kn für n€IN0
[1'] |{1, 4, 6, 20, 24}| = |{345, 2, -1, 33, 11}| = K5 = S(5)
Erst mit dieser Identifizierung S kann man Gleichungen [1] oben mit "=5" schreiben.
Die Kardintlität war oben nur für Mengen defininert.
Man kann diese Definition wohldefininert auf die Kardinalität selbst fortsetzen
Definition 2
Zu jeder Menge M sei |M| die Klasse der zu M gleichächtigen Mengen.
card(|M|):=|M| heiße Kardinalzahl von |M|.
Der wesentlich Unterschied zu Definition 1 ist der, dass wir nicht eine Menge zuordnen,
sondern eine Klasse.
Wohldefininertheit in Definition 2:
Für jede Menge M' aus Klasse |M| ist card(M') = |M'| = |M|
Damit ist die Zuordnung M' -> card(M') konstant auf |M|
und deswegen card(|M|):=|M| wohldefininert.
Definition 3
Sei K eine Unterklasse von KM, die aus Kardinalzahlen besteht.
1. Es sei
card(K) := K
2. Für jede Menge M sei card(|M|)<=card(K) genau dann,
wenn es eine Obermenge M'>=M gibt, die zur Klasse K gehört.
Wohldefininertheit in Definition 3:
zu 1.) Da Gleichmächtigkeit eine Äquivalentrelation in KM ist,
zerfällt KM genauso wie die Unterklasse K in wohlunterschiedene Äquivalenzklassen, bzw. Kardinalzahlen.
Mit Definition 2 wird jeder zu K gehörigen Kardinalzahl eindeutig sie selbst zugeordnet.
card(K) ist gerade die Gesamheit dieser Kardinalzahlen-weisen Zuordnungen.
zu 2.) Hier muss man die Verträglichkeit mit der Halbordnung der Kardinalzahlen zeigen
und wesentlich die Transitivität der "<="-Relation. Das mach ich jetzt nicht, weil
mehr fieselig als schwer.
Resultat:
Aus Definition 3, 1.) folgt card(KM) = KM
Aus Definition 3, 2.) folgt für jede Menge M ist card(M) = card(|M|) < card(KM),
denn card(|M|) = card(M) < card(P(M)) <= card(KM).
Dabei ist die letzte Ungleichheit "<" eine Aussage von Georg Cantor
http://de.wikipedia.org/wiki/Satz_von_Cantor
Signatur:
Beitrag zuletzt bearbeitet von Thomas der Große am 02.07.2013 um 22:39 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 84, Mitglied seit 10 Jahren |
Beitrag Nr. 2045-55
03.07.2013 06:41
|
Hallo Thomas,
Ich weiß, ich werfe immer alles in einen Topf.
Ein Beispiel noch.
Primzahlen sind Zahlen, die sich nicht durch Multiplikation ganzer Zahlen erreichen lassen.
Es gibt aber auch Dezimalzahlen, die sich nicht durch Division ganzer Zahlen erreichen lassen.
Dazu zählt auch 0,9 Periode 9.
Die 1 lässt sich aber durch Division gleicher ganzer Zahlen erreichen.
0,9 Periode 9 ist, wenn es um die Division ganzer Zahlen geht, eine unmögliche Periode.
10a-1a=9a
9:9=1
10 x 0,9 Periode 9 = 9,9 Periode 9.
9,9 Periode 9 - 0,9 Periode 9 = 9
9 : 9 = 1
0,9 Periode gleich 1.
Könnte ich so hinnehmen, wenn 0,9 Periode keine unmögliche Periode wäre.
Was soll also herauskommen, wenn ich eine Periode multipliziere, die nicht durch Division ganzer Zahlen erreichbar ist?
Das Ergebnis ist in diesem Rechenweg ein Annäherungswert, in diesem Fall 1.
Es gibt noch viel mehr Werte mit Nachkommastellen, die nicht durch Division ganzer Zahlen erreichbar sind.
Geht man mit diesen Werten den beschriebenen Rechenweg, so kommt immer nur ein Annäherungswert heraus.
Rechnet man mit Perioden, die durch Division ganzer Zahlen entstanden sind, so sieht die Rechnung wie im folgenden Beispiel aus:
4:3 = 1,3 Periode
10*1,3 Periode =13,3 Periode
13,3 Periode - 1,3 Periode = 12
12 : 9 = 1,3 Periode
Gleicher Rechenweg mit einer durch Divison entstandenen möglichen Periode ergibt wieder die Ursprungs-Periode.
Noch ein Beispiel für eine mögliche Periode.
10:11 = 0,9090 Periode.
Den oben beschriebenen Rechenweg halte ich jetzt nicht in seiner Gänze ein.
Die Periode zeichnet sich durch eine wiederkehrende Zahlenfolge nach dem Komma aus.Das mache ich mir zunutze.
Mit 10*0,9090 bekomme ich kein Ergebnis, bei dem der zehnte Teil passt.
Ich brauche 100 als Multiplikator.
100 * 0,9090 Periode = 90,90909090 usw.
90,90909090 - 0,90909090 = 90
An dieser Stelle erhalte ich eine ganze Zahl.
Ich musste nur dafür sorgen, daß der Multiplikator so angelegt ist, daß der zu subtrahierende Wert die Nachkommastellen entfernt.
Er muss übereinstimmen.
Die Rechnung ist aber noch nicht zu Ende.
Bis jetzt habe ich 100 * a - a
Jetzt muss ich aber noch schauen, was bei der Division passiert.
100 * a - a entspricht einem Multiplikator 99.
Nun muss ich die 90 durch 99 dividieren.
Ergebnis:0,9090909090 usw.Also Periode.
Es gibt keinen Zugewinn.
Bei dieser Rechnung gelange ich zum Ursprungswert zurück.
Warum geht das mit 0,9 Periode nicht?
Weil 0,9 Periode eine, wenn es um Division ganzer Zahlen geht, unmögliche Periode ist.
Jede Periode, die hinter dem Komma unendlich viele 9 aufweist, ist eine unmögliche Periode.
Wie z.B. 1,9 Periode, 2,9 Periode usw.
Multipliziert man die unmögliche Periode 0,9 mit 10, so erhöht man nur die unmögliche Periode.
Von der verzehnfachten unmöglichen Periode wird 1/10 ihrer Wertigkeitkeit abgezogen.
Es entsteht eine ganze Zahl.
Wenn ich 0,9 Periode nicht durch Division erreiche, komme ich auch nicht durch Multiplikation zum Ursprung zurück.
Ich kann sie nicht erreichen.
0,9 Periode ist nicht gleich 1.
Der vorliegende Rechenweg rundet die 0,9 Periode ungefragt auf.
Der unmöglichen Periode wird eine weitere unmögliche Periode hinzu addiert.
Es ist die 0,0 Periode o gefolgt von einer 1.
In diesem Fall ist es so, daß zwei unmögliche Perioden eine mögliche Zahl ergeben.
Der Rechenweg rundet in diesem Fall auf die nächst mögliche Zahl auf.
Es gibt einen Zugewinn.Wahrheit ist frei von Vermutung.
Theorie ist immer eine formulierte Vermutung.
Ich weiß, ich werfe immer alles in einen Topf.
Ein Beispiel noch.
Primzahlen sind Zahlen, die sich nicht durch Multiplikation ganzer Zahlen erreichen lassen.
Es gibt aber auch Dezimalzahlen, die sich nicht durch Division ganzer Zahlen erreichen lassen.
Dazu zählt auch 0,9 Periode 9.
Die 1 lässt sich aber durch Division gleicher ganzer Zahlen erreichen.
0,9 Periode 9 ist, wenn es um die Division ganzer Zahlen geht, eine unmögliche Periode.
10a-1a=9a
9:9=1
10 x 0,9 Periode 9 = 9,9 Periode 9.
9,9 Periode 9 - 0,9 Periode 9 = 9
9 : 9 = 1
0,9 Periode gleich 1.
Könnte ich so hinnehmen, wenn 0,9 Periode keine unmögliche Periode wäre.
Was soll also herauskommen, wenn ich eine Periode multipliziere, die nicht durch Division ganzer Zahlen erreichbar ist?
Das Ergebnis ist in diesem Rechenweg ein Annäherungswert, in diesem Fall 1.
Es gibt noch viel mehr Werte mit Nachkommastellen, die nicht durch Division ganzer Zahlen erreichbar sind.
Geht man mit diesen Werten den beschriebenen Rechenweg, so kommt immer nur ein Annäherungswert heraus.
Rechnet man mit Perioden, die durch Division ganzer Zahlen entstanden sind, so sieht die Rechnung wie im folgenden Beispiel aus:
4:3 = 1,3 Periode
10*1,3 Periode =13,3 Periode
13,3 Periode - 1,3 Periode = 12
12 : 9 = 1,3 Periode
Gleicher Rechenweg mit einer durch Divison entstandenen möglichen Periode ergibt wieder die Ursprungs-Periode.
Noch ein Beispiel für eine mögliche Periode.
10:11 = 0,9090 Periode.
Den oben beschriebenen Rechenweg halte ich jetzt nicht in seiner Gänze ein.
Die Periode zeichnet sich durch eine wiederkehrende Zahlenfolge nach dem Komma aus.Das mache ich mir zunutze.
Mit 10*0,9090 bekomme ich kein Ergebnis, bei dem der zehnte Teil passt.
Ich brauche 100 als Multiplikator.
100 * 0,9090 Periode = 90,90909090 usw.
90,90909090 - 0,90909090 = 90
An dieser Stelle erhalte ich eine ganze Zahl.
Ich musste nur dafür sorgen, daß der Multiplikator so angelegt ist, daß der zu subtrahierende Wert die Nachkommastellen entfernt.
Er muss übereinstimmen.
Die Rechnung ist aber noch nicht zu Ende.
Bis jetzt habe ich 100 * a - a
Jetzt muss ich aber noch schauen, was bei der Division passiert.
100 * a - a entspricht einem Multiplikator 99.
Nun muss ich die 90 durch 99 dividieren.
Ergebnis:0,9090909090 usw.Also Periode.
Es gibt keinen Zugewinn.
Bei dieser Rechnung gelange ich zum Ursprungswert zurück.
Warum geht das mit 0,9 Periode nicht?
Weil 0,9 Periode eine, wenn es um Division ganzer Zahlen geht, unmögliche Periode ist.
Jede Periode, die hinter dem Komma unendlich viele 9 aufweist, ist eine unmögliche Periode.
Wie z.B. 1,9 Periode, 2,9 Periode usw.
Multipliziert man die unmögliche Periode 0,9 mit 10, so erhöht man nur die unmögliche Periode.
Von der verzehnfachten unmöglichen Periode wird 1/10 ihrer Wertigkeitkeit abgezogen.
Es entsteht eine ganze Zahl.
Wenn ich 0,9 Periode nicht durch Division erreiche, komme ich auch nicht durch Multiplikation zum Ursprung zurück.
Ich kann sie nicht erreichen.
0,9 Periode ist nicht gleich 1.
Der vorliegende Rechenweg rundet die 0,9 Periode ungefragt auf.
Der unmöglichen Periode wird eine weitere unmögliche Periode hinzu addiert.
Es ist die 0,0 Periode o gefolgt von einer 1.
In diesem Fall ist es so, daß zwei unmögliche Perioden eine mögliche Zahl ergeben.
Der Rechenweg rundet in diesem Fall auf die nächst mögliche Zahl auf.
Es gibt einen Zugewinn.
Signatur:
Theorie ist immer eine formulierte Vermutung.
Beitrag zuletzt bearbeitet von Jense am 03.07.2013 um 09:22 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 1.375, Mitglied seit 16 Jahren |
Beitrag Nr. 2045-56
03.07.2013 10:15
|
Thomas der Große schrieb in Beitrag Nr. 2045-54:Definition 2
Zu jeder Menge M sei |M| die Klasse der zu M gleichächtigen Mengen.
card(|M|):=|M| heiße Kardinalzahl von |M|.
Der wesentlich Unterschied zu Definition 1 ist der, dass wir nicht eine Menge zuordnen,
sondern eine Klasse.
Wohldefininertheit in Definition 2:
Für jede Menge M' aus Klasse |M| ist card(M') = |M'| = |M|
Damit ist die Zuordnung M' -> card(M') konstant auf |M|
und deswegen card(|M|):=|M| wohldefininert.
Hallo Thomas,
danke für diese ausführliche Darstellung. Ich denke, ich habe jetzt den Unterschied zwischen Menge und Klasse begriffen. Vermutlich hast du im Gegensatz zu mir Mathematik als Hauptfach studiert. Denn ein Laie kann dieses schwierige Thema nicht so gut darstellen wie du es hier getan hast.
M.f.G. Eugen Bauhof
Signatur:
der Normale aus seinen Erfahrungen,
und der Dumme weiß alles besser.
Sokrates.
[Gäste dürfen nur lesen]
| Beiträge: 1.375, Mitglied seit 16 Jahren |
Beitrag Nr. 2045-57
03.07.2013 11:17
|
Jense schrieb in Beitrag Nr. 2045-55:Multipliziert man die unmögliche Periode 0,9 mit 10, so erhöht man nur die unmögliche Periode.
Hallo Jense,
woher hast du den Ausdruck unmögliche Periode? Ist das ein Standardausdruck in der Mathematik?
M.f.G. Eugen Bauhof
Signatur:
der Normale aus seinen Erfahrungen,
und der Dumme weiß alles besser.
Sokrates.
[Gäste dürfen nur lesen]
| Beiträge: 84, Mitglied seit 10 Jahren |
Beitrag Nr. 2045-58
03.07.2013 14:41
|
Hallo Eugen,
es ist kein Standardausdruck.
Ich habe sie so genannt, weil es ihre Eigenschaft ist.
Die Eigenschaft trifft nur unter der genannten Bedingung zu.
Eine Primzahl ist ja auch an Bedingungen geknüpft.
Eine Primzahl lässt sich nicht durch Multiplikation ganzer Zahlen, von der keine selbst schon die Primzahl darstellt, erreichen.
Sie ist größer als 1, ist nur durch 1 und durch sich selbst teilbar.
Die genannte Periode lässt sich nicht durch Division ganzer Zahlen erreichen.
Vervielfacht man eine unmögliche Periode, so ist das Ergebnis eine höhere unmögliche Periode.
Vervielfacht man eine Primzahl, ist das Ergebnis keine weitere Primzahl.
Eine unmögliche Periode ist sozusagen das Gegenstück zur Primzahl.
Die 1 lässt sich wohl durch Division gleicher Zahlen erreichen.
0,9 Periode lässt sich nicht durch Divison ganzer Zahlen erreichen.
Wenn zwei Zahlen nicht der gleichen Bedingung unterliegen, können sie in ihrer Eigenschaft nicht gleich sein.
Gruß, Jense.Wahrheit ist frei von Vermutung.
Theorie ist immer eine formulierte Vermutung.
es ist kein Standardausdruck.
Ich habe sie so genannt, weil es ihre Eigenschaft ist.
Die Eigenschaft trifft nur unter der genannten Bedingung zu.
Eine Primzahl ist ja auch an Bedingungen geknüpft.
Eine Primzahl lässt sich nicht durch Multiplikation ganzer Zahlen, von der keine selbst schon die Primzahl darstellt, erreichen.
Sie ist größer als 1, ist nur durch 1 und durch sich selbst teilbar.
Die genannte Periode lässt sich nicht durch Division ganzer Zahlen erreichen.
Vervielfacht man eine unmögliche Periode, so ist das Ergebnis eine höhere unmögliche Periode.
Vervielfacht man eine Primzahl, ist das Ergebnis keine weitere Primzahl.
Eine unmögliche Periode ist sozusagen das Gegenstück zur Primzahl.
Die 1 lässt sich wohl durch Division gleicher Zahlen erreichen.
0,9 Periode lässt sich nicht durch Divison ganzer Zahlen erreichen.
Wenn zwei Zahlen nicht der gleichen Bedingung unterliegen, können sie in ihrer Eigenschaft nicht gleich sein.
Gruß, Jense.
Signatur:
Theorie ist immer eine formulierte Vermutung.
Beitrag zuletzt bearbeitet von Jense am 04.07.2013 um 23:58 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 84, Mitglied seit 10 Jahren |
Beitrag Nr. 2045-59
22.07.2013 03:22
|
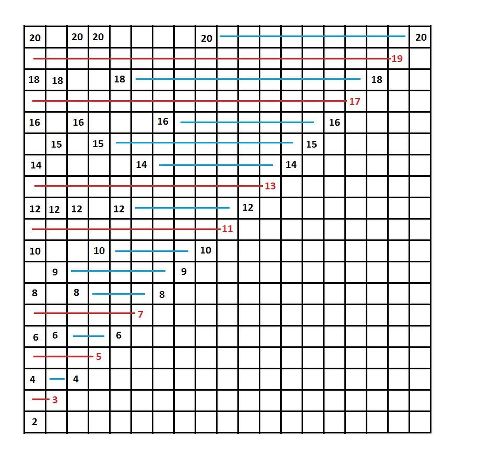
Ich wußte nicht wohin damit, aber es hat ja auch mit Mathematik und Unendlichkeit zu tun.
Die Zeichnung zeigt eine Primzahlen-Tabelle, bei der nicht mehr nachgerechnet werden muss, ob es sich bei einer Zahl um eine Primzahl handelt.
Da eine Primzahl in keiner vorhergehenden Malfolge vorkam, steht sie in einer Zeile ganz rechts für sich allein.
Man kann in dieser Zeile einen durchgehenden Strich nach links ziehen, ohne noch einmal auf den gleichen Wert zu treffen.
Bis hierher eigentlich nichts Besonderes.
Anders sieht es aus, wenn ich gar keine echten Zahlen eintrage.
Dazu nehme ich mir kariertes Papier und einen Bleistift.
In der ersten Spalte male ich das unterste Karo aus.Also dort, wo jetzt die 2 zu sehen ist.
Zähle 2 Karos in der gleichen Spalte nach oben und male dieses Karo ebenfalls aus.
Das kann ich beliebig oft wiederholen.
In der Spalte rechts daneben beginne ich damit, daß ich das zweite Karo von unten, dort wo jetzt nach die 3 zu sehen ist, auszumalen.
Nun zähle ich 3 Karos nach oben und male dieses Karo aus.
Nach diesem Prinzip kann ich in der Tabelle alle Zahlen übermalen.
Ich könnte aber auch Folgendes tun.
Ich nehme kein kariertes Papier sondern einen Zirkel und Lineal.
Damit kann ich das Gleiche erreichen, ohne jemals eine Zahl zu Papier zu bringen.
Für die erste Spalte stelle ich am Zirkel einen Radius von 2cm ein.Für die zweite Zeile 3cm usw.
Stellt man die Mathematik als eindimensionalen Strang dar, also 1 2 3 4 5 6 usw, muss man jede Zahl rechnerisch überprüfen, ob sie eine Primzahl ist.
Eine Tabelle stellt Mathematik in zwei Dimensionen dar.
Dadurch, daß die Mathematik verzweidimensionalisiert wurde, geben sich die Primzahlen zu erkennen.
Wenn ich die Tabelle ausfüllen kann, ohne nachrechnen zu müssen, dann zeigt die Tabelle, daß die Anordnung der Primzahlen auf einem geometrischen Prinzip beruht.
Wenn ich alle Zahlen in dieser Tabelle unkenntlich mache, kann ich trotzdem noch sehen, wo sich eine Primzahl befindet.
Ich kann zwar nicht sagen welche, aber wo im System.
Theoretisch kann man mit Lineal und Zirkel ermitteln, wo sich eine Primzahl befindet.
Gehe ich mit Lineal und Zirkel zu Werke, muss ich nur r+1 rechnen können.
Denn der Radius wird am Zirkel immer nur um 1cm vergrößert.
Das heißt, ich muss eigentlich nicht rechnen können, ich muss nur den eindimensionalen Strang der Mathematik kennen.
Schneide ich den Teil der Tabelle ab, in dem sich nur leere Felder befinden, so erhalte ich ein rechtwinkliges Dreieck.
Obwohl sich gleiche Werte immer in "Augenhöhe" gegenüber stehen, sich in der gleichen Zeile befinden, zeigt die Tabelle trotzdem geordnetes Chaos.
Warum?
Weil der Abstand der Werte von Zeile zu Zeile variiert.Es gibt keine Ordnung.
Vergleicht man z.B. die Zeilen für 15 und 16, die unmittelbar zusammenliegen, so kann kaum vorhergesagt werden, wo in der Zeile die nächste 15 auftauchen wird.
Das Gleiche dann in der Zeile für die 16.
Die Tabelle wurde so angelegt, daß sie eine Bedingung erfüllt: Das Aufspüren von Primzahlen.
Aus dieser Ordnung entsteht innerhalb der Tabelle Chaos.
Rein theoretisch müsste man Chaos ordnen können, wenn man dafür die erforderliche Tabelle erstellt.
Eine Tabelle muss nicht nur quadratisch oder dreieckig sein.
Die Form ergibt sich aus Erwartung und Anforderung.
Es könnte sogar eine dreidimensionale Tabelle sein.
Signatur:
Theorie ist immer eine formulierte Vermutung.
Beitrag zuletzt bearbeitet von Jense am 22.07.2013 um 04:35 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 1.566, Mitglied seit 11 Jahren |
Beitrag Nr. 2045-60
22.07.2013 10:56
|
Jense schrieb in Beitrag Nr. 2045-55:
Primzahlen sind Zahlen, die sich nicht durch Multiplikation ganzer Zahlen erreichen lassen.
Es gibt aber auch Dezimalzahlen, die sich nicht durch Division ganzer Zahlen erreichen lassen.
Die 1 lässt sich aber durch Division gleicher ganzer Zahlen erreichen.
0,9 Periode 9 ist, wenn es um die Division ganzer Zahlen geht, eine unmögliche Periode.
Die 1 und auch 0,9 Periode 9 sind einfach nur verschiedene Dezimaldarstellungen der Zahl 1.
Jede Zahl, die durch einen endlichen Dezimalbruch darstellbar ist, hat stets auch Darstellungen in Form unendlich langer Dezimalbrüche.
Die Mathematik kennt keinen Begriff "unmögliche Periode" (denn jede unendlich lange Dezimalzahl ist Notation einer konvergenten Reihe; die Summe, die diese Reihe darstellt, ist der Wert des unendlich langen Dezimalbruchs).
Beitrag zuletzt bearbeitet von Grtgrt am 22.07.2013 um 11:08 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 84, Mitglied seit 10 Jahren |
Beitrag Nr. 2045-61
22.07.2013 11:13
|
Die Division welcher ganzen Zahlen ergibt 0,9 Periode?
0,9Periode ist gleich 1,0 Periode 0 ?
Für mich sind Zahlen- auch Dezimalzahlen - absolute Werte, keine Annäherungswerte.Wahrheit ist frei von Vermutung.
Theorie ist immer eine formulierte Vermutung.
0,9Periode ist gleich 1,0 Periode 0 ?
Für mich sind Zahlen- auch Dezimalzahlen - absolute Werte, keine Annäherungswerte.
Signatur:
Theorie ist immer eine formulierte Vermutung.
[Gäste dürfen nur lesen]
| Beiträge: 1.566, Mitglied seit 11 Jahren |
Beitrag Nr. 2045-62
22.07.2013 11:20
|
Jense schrieb in Beitrag Nr. 2045-61:
0,9 Periode 9 ist gleich 1,0 Periode 0 ?
Ja, das ist richtig.
[Gäste dürfen nur lesen]
| Beiträge: 1.375, Mitglied seit 16 Jahren |
Beitrag Nr. 2045-63
22.07.2013 15:44
|
Jense schrieb in Beitrag Nr. 2045-59:
Ich wußte nicht wohin damit, aber es hat ja auch mit Mathematik und Unendlichkeit zu tun.
Die Zeichnung zeigt eine Primzahlen-Tabelle, bei der nicht mehr nachgerechnet werden muss, ob es sich bei einer Zahl um eine Primzahl handelt.
Da eine Primzahl in keiner vorhergehenden Malfolge vorkam, steht sie in einer Zeile ganz rechts für sich allein.
Man kann in dieser Zeile einen durchgehenden Strich nach links ziehen, ohne noch einmal auf den gleichen Wert zu treffen.
Bis hierher eigentlich nichts Besonderes.
Hallo Jense,
auf welcher Methode beruht deine Tabelle zum Auffinden von Primzahlen? Ich vermute, auf der Sieb-Methode des Erasthostenes.
Oder hast du eine neue Methode erfunden? Wenn ja, dann bitte ich um nähere Erläuterung dieser neuen Methode. Denn dann könnte ich ein FORTRAN-Programm schreiben, um zu prüfen, ob deine neue Methode zum Auffinden von Primzahlen schneller ist als die Sieb-Methode.
M.f.G. Eugen Bauhof
Signatur:
der Normale aus seinen Erfahrungen,
und der Dumme weiß alles besser.
Sokrates.
[Gäste dürfen nur lesen]
In diesem Forum dürfen nur Mitglieder schreiben. Hier kannst du dich anmelden




 Nach oben
Nach oben