Zwillingsparadoxon
Thema erstellt von Derfragende
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 13-342
15.03.2015 17:32
|
Hallo Bauhof,
Ursache für den Altersunterschied sind gemäß SRT die "unterschiedlichen Auffassungen über die Gleichzeitigkeit von Ereignissen an entfernten Orten". Ich denke darüber sind wir uns einig. Dazu, dass dieser Altersunterschied schließlich widerspruchsfrei beobachtet werden kann, tragen jedoch die Lichtlaufzeiten wie folgt bei:
B fliege aus Sicht A mit v = 0,6c in 1,2 Lj Entfernung und kehre dort um.
Sicht A: Während der Hin- und Rückreise vergehen für A 4Jahre und für B 3,2 Jahre .
Sicht B: Während der Hin- und Rückreise vergehen für A 2,56 Jahre und für B 3,2 Jahre.
Die beiden o.a. Sichten wären widerspruchsfrei nur dann miteinander vereinbar, wenn B bei Uhr A am Umkehrpunkt einen Zeitsprung von 1,44 Jahren feststellen könnte.
Ein derartiger Zeitsprung wird von B aber nicht beobachtet. Statt dessen beobachtet B auf der Hinreise den Gang der Uhr von A mit dem Faktor 0,5 und auf der Rückreise mit dem Faktor 2. Auf der Hinreise beobachtet B also eine Alterung von A um 0,8 Jahre, auf der Rückreise dagegen um 3,2 Jahre.
Dieser beobachtete Unterschied des Ganges der Uhren auf der Hin- und Rückreise ist durch die verschiedenen Lichtlaufzeiten bewirkt. Folglich bewirken diese nach meiner Auffassung, dass beide Zwillinge beim Wiedersehen widerspruchsfrei feststellen, dass A um 4 Jahre und nicht um 2,56 Jahre gealtert ist.
Bauhof schrieb in Beitrag Nr. 13-341:tragen diese von dir genannten unterschiedlichen Lichtlaufzeiten in irgendeiner Weise für den Altersunterschied bei, wenn sich die Zwillinge wieder getroffen haben?
Ursache für den Altersunterschied sind gemäß SRT die "unterschiedlichen Auffassungen über die Gleichzeitigkeit von Ereignissen an entfernten Orten". Ich denke darüber sind wir uns einig. Dazu, dass dieser Altersunterschied schließlich widerspruchsfrei beobachtet werden kann, tragen jedoch die Lichtlaufzeiten wie folgt bei:
B fliege aus Sicht A mit v = 0,6c in 1,2 Lj Entfernung und kehre dort um.
Sicht A: Während der Hin- und Rückreise vergehen für A 4Jahre und für B 3,2 Jahre .
Sicht B: Während der Hin- und Rückreise vergehen für A 2,56 Jahre und für B 3,2 Jahre.
Die beiden o.a. Sichten wären widerspruchsfrei nur dann miteinander vereinbar, wenn B bei Uhr A am Umkehrpunkt einen Zeitsprung von 1,44 Jahren feststellen könnte.
Ein derartiger Zeitsprung wird von B aber nicht beobachtet. Statt dessen beobachtet B auf der Hinreise den Gang der Uhr von A mit dem Faktor 0,5 und auf der Rückreise mit dem Faktor 2. Auf der Hinreise beobachtet B also eine Alterung von A um 0,8 Jahre, auf der Rückreise dagegen um 3,2 Jahre.
Dieser beobachtete Unterschied des Ganges der Uhren auf der Hin- und Rückreise ist durch die verschiedenen Lichtlaufzeiten bewirkt. Folglich bewirken diese nach meiner Auffassung, dass beide Zwillinge beim Wiedersehen widerspruchsfrei feststellen, dass A um 4 Jahre und nicht um 2,56 Jahre gealtert ist.
Beitrag zuletzt bearbeitet von Claus am 15.03.2015 um 17:36 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 1.375, Mitglied seit 16 Jahren |
Beitrag Nr. 13-343
15.03.2015 18:12
|
Claus schrieb in Beitrag Nr. 13-342:Ursache für den Altersunterschied sind gemäß SRT die "unterschiedlichen Auffassungen über die Gleichzeitigkeit von Ereignissen an entfernten Orten". Ich denke darüber sind wir uns einig. Dazu, dass dieser Altersunterschied schließlich widerspruchsfrei beobachtet werden kann, tragen jedoch die Lichtlaufzeiten wie folgt bei: ...
Hallo Claus,
ich verstehe leider nicht auf was du hinauswillst. Der Altersunterschied doch wird widerspruchsfrei beobachtet bei der Rückkehr des reisenden Zwillings, indem die Zwillinge ihre mitgeführten Uhren vergleichen. Außerdem stimme ich dem zu, was Okotombrok geschrieben hat:
Okotombrok schrieb in Beitrag Nr. 13-333:Der mathematische Formalismus zur Berechnung der Zeitdilatation erfordert keine Lichtlaufzeiten. Die Zeitdilatation ist das, was übrig bleibt, wenn man die Lichtlaufzeiten herausrechnet.
Die Zeitdilatation und damit der Altersunterschied der Zwillinge begründet sich allein in der physikalischen Geometrie der relativistischen Raumzeit.
M.f.G. Eugen Bauhof
Signatur:
der Normale aus seinen Erfahrungen,
und der Dumme weiß alles besser.
Sokrates.
Beitrag zuletzt bearbeitet von Bauhof am 15.03.2015 um 18:23 Uhr.
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 13-344
15.03.2015 20:21
|
Hallo Bauhof,
B reist mit konstantem Geschwindigkeitsbetrag. Die Uhr von B läuft kontinuierlich um 3,2 Jahre vorwärts und macht dabei keine Zeitsprünge. B macht keinerlei Pause am Umkehrpunkt. Auch die Uhr von A läuft kontinuierlich, nämlich um 4 Jahre vorwärts und macht ebenfalls keinerlei Zeitsprünge.
Gemäß SRT bewirkt die Zeitdilatation aus der Sicht von B aber, dass die Uhr von A während des 3,2jährigen Hin- und Rückflugs mit dem Faktor 0,8, also um 2,56 Jahre vorrückt.
Frage: Wie erklärt sich deiner Meinung nach ohne Berücksichtigung der Lichtlaufzeit der beim Uhrenvergleich festgestellte Altersunterschied von 4 anstelle von 2,56 Jahren?
Bauhof schrieb in Beitrag Nr. 13-343:Der Altersunterschied doch wird widerspruchsfrei beobachtet bei der Rückkehr des reisenden Zwillings, indem die Zwillinge ihre mitgeführten Uhren vergleichen. ...
Die Zeitdilatation und damit der Altersunterschied der Zwillinge begründet sich allein in der physikalischen Geometrie der relativistischen Raumzeit.
B reist mit konstantem Geschwindigkeitsbetrag. Die Uhr von B läuft kontinuierlich um 3,2 Jahre vorwärts und macht dabei keine Zeitsprünge. B macht keinerlei Pause am Umkehrpunkt. Auch die Uhr von A läuft kontinuierlich, nämlich um 4 Jahre vorwärts und macht ebenfalls keinerlei Zeitsprünge.
Gemäß SRT bewirkt die Zeitdilatation aus der Sicht von B aber, dass die Uhr von A während des 3,2jährigen Hin- und Rückflugs mit dem Faktor 0,8, also um 2,56 Jahre vorrückt.
Frage: Wie erklärt sich deiner Meinung nach ohne Berücksichtigung der Lichtlaufzeit der beim Uhrenvergleich festgestellte Altersunterschied von 4 anstelle von 2,56 Jahren?
Beitrag zuletzt bearbeitet von Claus am 15.03.2015 um 20:30 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 936, Mitglied seit 13 Jahren |
Beitrag Nr. 13-345
15.03.2015 21:14
|
Was bleibt - von der Zeitdilatation, ist höflich ausgedrückt, ein Beobachtungstheater.
Eine Vereinigung der Relativitätstheorie mit der Quantenmechanik wird wohl am besten zu erreichen sein,
wenn man erstere sang und klanglos in einer Versenkung verschwinden lässt.Es gibt nur eine Zeit - die aktive und die passive Gegenwart - und Gravitation
ist die Antwort der Gegenwart auf die Einwirkung vergangener Wichtigkeiten.
Eine Vereinigung der Relativitätstheorie mit der Quantenmechanik wird wohl am besten zu erreichen sein,
wenn man erstere sang und klanglos in einer Versenkung verschwinden lässt.
Signatur:
ist die Antwort der Gegenwart auf die Einwirkung vergangener Wichtigkeiten.
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 13-346
15.03.2015 21:27
|
Hallo Harald Denifle,
Während wir mit Argumenten unser jeweiliges Verständnis darlegen, bringst du hier Polemik. Was soll das bewirken?
Durch unbegründete Ironie lassen sich nur diejenigen beeindrucken, die selbst nicht nachdenken - und die magst du meinetwegen ruhig überzeugen.
Harald Denifle schrieb in Beitrag Nr. 13-345:Was bleibt - von der Zeitdilatation, ist höflich ausgedrückt, ein Beobachtungstheater.
Während wir mit Argumenten unser jeweiliges Verständnis darlegen, bringst du hier Polemik. Was soll das bewirken?
Zitat von Harald Denifle:Eine Vereinigung der Relativitätstheorie mit der Quantenmechanik wird wohl am besten zu erreichen sein,
wenn man erstere sang und klanglos in einer Versenkung verschwinden lässt.
Durch unbegründete Ironie lassen sich nur diejenigen beeindrucken, die selbst nicht nachdenken - und die magst du meinetwegen ruhig überzeugen.
[Gäste dürfen nur lesen]
| Beiträge: 1.477, Mitglied seit 16 Jahren |
Beitrag Nr. 13-347
15.03.2015 22:06
|
Hallo Claus,
richtig, wenn A berücksichtigt, dass für B, der sich auf den Wendepunkt zubewegt, die Entfernung verkürzt ist (Lorentzkontraktion), für ihn selber aber nicht.
Hier berücksichtigt B aber nicht, dass A zum Wendepunkt ruht und eine größere Entfernung misst.
Ich denke, dass die beiden Sichtweisen die du aufführst nicht unter gleichen Bedingungen betrachtet sind.
Wenn beide Kontrahenten die Längenkontraktion in Bewegungsrichtung berücksichtigen und die unterschiedlichen Entfernungen, A–Wendepunkt versus B–Wendepunkt als Berechnungsgrundlage zugrunde legen, dann kommen sie doch zum gleichen Ergebnis, was den Altersunterschied anbelangt.
Äh? meintest du vielleicht einen Altersunterschied von 0,8 anstelle von 1,44 Jahren?
Wie dem auch sei, meine Ansicht dazu habe ich oben geschrieben.
mfg okotombrok"Der Kopf ist rund, damit die Gedanken die Richtung wechseln können"
(Francis Picabia)
Claus schrieb in Beitrag Nr. 13-342:B fliege aus Sicht A mit v = 0,6c in 1,2 Lj Entfernung und kehre dort um.
Sicht A: Während der Hin- und Rückreise vergehen für A 4Jahre und für B 3,2 Jahre .
richtig, wenn A berücksichtigt, dass für B, der sich auf den Wendepunkt zubewegt, die Entfernung verkürzt ist (Lorentzkontraktion), für ihn selber aber nicht.
Zitat:Sicht B: Während der Hin- und Rückreise vergehen für A 2,56 Jahre und für B 3,2 Jahre.
Hier berücksichtigt B aber nicht, dass A zum Wendepunkt ruht und eine größere Entfernung misst.
Ich denke, dass die beiden Sichtweisen die du aufführst nicht unter gleichen Bedingungen betrachtet sind.
Wenn beide Kontrahenten die Längenkontraktion in Bewegungsrichtung berücksichtigen und die unterschiedlichen Entfernungen, A–Wendepunkt versus B–Wendepunkt als Berechnungsgrundlage zugrunde legen, dann kommen sie doch zum gleichen Ergebnis, was den Altersunterschied anbelangt.
Zitat von Claus:Frage: Wie erklärt sich deiner Meinung nach ohne Berücksichtigung der Lichtlaufzeit der beim Uhrenvergleich festgestellte Altersunterschied von 4 anstelle von 2,56 Jahren?
Äh? meintest du vielleicht einen Altersunterschied von 0,8 anstelle von 1,44 Jahren?
Wie dem auch sei, meine Ansicht dazu habe ich oben geschrieben.
mfg okotombrok
Signatur:
(Francis Picabia)
[Gäste dürfen nur lesen]
|
Stueps (Moderator)
Beiträge: 3.477, Mitglied seit 18 Jahren
|
Beitrag Nr. 13-348
15.03.2015 22:25
|
Hallo Okotombrok,
Muss er m.E. nicht, denn es geht um seine Sicht:
B braucht eben nur 3,2 Jahre aus seiner Sicht. Und in dieser seiner Zeit vergehen aus seiner Sicht eben nur 2,56 Jahre auf der Uhr von A.
Natürlich nicht, denn sie sind ja nicht im selben Bezugssystem. Aber das hat ja Claus oben auch vorgerechnet.
Das verstehe ich wiederum nicht. Kannst du das im Stile von Claus konkret vorrechnen? Aus irgendeinem Grunde verstehe ich das dann, kann es nachvollziehen.
Beste GrüßeDiese Welt gibt es nur, weil es Regeln gibt.
Okotombrok schrieb in Beitrag Nr. 13-347:Hier berücksichtigt B aber nicht, dass A zum Wendepunkt ruht und eine größere Entfernung misst.
Muss er m.E. nicht, denn es geht um seine Sicht:
B braucht eben nur 3,2 Jahre aus seiner Sicht. Und in dieser seiner Zeit vergehen aus seiner Sicht eben nur 2,56 Jahre auf der Uhr von A.
Okotombrok schrieb in Beitrag Nr. 13-347:Ich denke, dass die beiden Sichtweisen die du aufführst nicht unter gleichen Bedingungen betrachtet sind.
Natürlich nicht, denn sie sind ja nicht im selben Bezugssystem. Aber das hat ja Claus oben auch vorgerechnet.
Okotombrok schrieb in Beitrag Nr. 13-347:Wenn beide Kontrahenten die Längenkontraktion in Bewegungsrichtung berücksichtigen und die unterschiedlichen Entfernungen, A–Wendepunkt versus B–Wendepunkt als Berechnungsgrundlage zugrunde legen, dann kommen sie doch zum gleichen Ergebnis, was den Altersunterschied anbelangt.
Das verstehe ich wiederum nicht. Kannst du das im Stile von Claus konkret vorrechnen? Aus irgendeinem Grunde verstehe ich das dann, kann es nachvollziehen.
Beste Grüße
Signatur:
Beitrag zuletzt bearbeitet von Stueps am 15.03.2015 um 22:30 Uhr.
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 13-349
15.03.2015 23:15
|
Hallo Okotombrok,
Nein ich meinte den Altersunterschied von A zwischen Start und Ende der Reise. Dieser beträgt 4 Jahre.
Wieso meinst du, dass B das nicht berücksichtigt? B geht aufgrund der Lorentz-Kontraktion selbstverständlich davon aus, dass er eine geringere Distanz zu durchfliegen hat, nämlich nur 1,92 Lj anstatt 2,4 Lj (wie A es annimmt). Aus diesem Grund berechnet B ja auch korrekt, dass er für die Reise 3,2 Jahre benötigen wird. Um diese Zeit rückt die Uhr von B also während der Reise vor. Die Zeitdilatation, die B bei A berechnet, führt jedoch ungeachtet der aus Sicht B geringeren Distanz dazu, dass bei A während der 3,2jährigen Reise nur 2,56 Jahre vergehen. Daher müsste A doch während der Dauer des Hin- und Rückflugs auch nur diese 2,56 Jahre gealtert sein. Tatsächlich ist er aber um 4 Jahre gealtert. Daher die an Bauhof gerichtete Frage auch an dich, der du dich einmal in die Lage von B versetzen mögest: Wie erklärst du das?
Okotombrok schrieb in Beitrag Nr. 13-347:Äh? meintest du vielleicht einen Altersunterschied von 0,8 anstelle von 1,44 Jahren?
Nein ich meinte den Altersunterschied von A zwischen Start und Ende der Reise. Dieser beträgt 4 Jahre.
Zitat von Okotombrok:Hier berücksichtigt B aber nicht, dass A zum Wendepunkt ruht und eine größere Entfernung misst.
Ich denke, dass die beiden Sichtweisen die du aufführst nicht unter gleichen Bedingungen betrachtet sind.
Wenn beide Kontrahenten die Längenkontraktion in Bewegungsrichtung berücksichtigen und die unterschiedlichen Entfernungen, A–Wendepunkt versus B–Wendepunkt als Berechnungsgrundlage zugrunde legen, dann kommen sie doch zum gleichen Ergebnis, was den Altersunterschied anbelangt.
Wieso meinst du, dass B das nicht berücksichtigt? B geht aufgrund der Lorentz-Kontraktion selbstverständlich davon aus, dass er eine geringere Distanz zu durchfliegen hat, nämlich nur 1,92 Lj anstatt 2,4 Lj (wie A es annimmt). Aus diesem Grund berechnet B ja auch korrekt, dass er für die Reise 3,2 Jahre benötigen wird. Um diese Zeit rückt die Uhr von B also während der Reise vor. Die Zeitdilatation, die B bei A berechnet, führt jedoch ungeachtet der aus Sicht B geringeren Distanz dazu, dass bei A während der 3,2jährigen Reise nur 2,56 Jahre vergehen. Daher müsste A doch während der Dauer des Hin- und Rückflugs auch nur diese 2,56 Jahre gealtert sein. Tatsächlich ist er aber um 4 Jahre gealtert. Daher die an Bauhof gerichtete Frage auch an dich, der du dich einmal in die Lage von B versetzen mögest: Wie erklärst du das?
Beitrag zuletzt bearbeitet von Claus am 15.03.2015 um 23:17 Uhr.
[Gäste dürfen nur lesen]
| Beiträge: 1.375, Mitglied seit 16 Jahren |
Beitrag Nr. 13-350
16.03.2015 11:06
|
Claus schrieb in Beitrag Nr. 13-344:B reist mit konstantem Geschwindigkeitsbetrag. Die Uhr von B läuft kontinuierlich um 3,2 Jahre vorwärts und macht dabei keine Zeitsprünge. B macht keinerlei Pause am Umkehrpunkt. Auch die Uhr von A läuft kontinuierlich, nämlich um 4 Jahre vorwärts und macht ebenfalls keinerlei Zeitsprünge.
Gemäß SRT bewirkt die Zeitdilatation aus der Sicht von B aber, dass die Uhr von A während des 3,2jährigen Hin- und Rückflugs mit dem Faktor 0,8, also um 2,56 Jahre vorrückt.
Frage: Wie erklärt sich deiner Meinung nach ohne Berücksichtigung der Lichtlaufzeit der beim Uhrenvergleich festgestellte Altersunterschied von 4 anstelle von 2,56 Jahren?
Hallo Claus,
mit diesen Zahlen kann ich momentan nichts anfangen. Bitte teile mir die Zahlen deines Zwillingsexperiments in folgender Form mit:
1. Geschwindigkeit v des reisenden Zwillings aus der Sicht des ruhenden Zwillings.
2. Entfernung s des Umkehrpunktes aus der Sicht des ruhenden Zwillings.
Dann werde ich den Altersunterschied berechnen.
M.f.G. Eugen Bauhof
Signatur:
der Normale aus seinen Erfahrungen,
und der Dumme weiß alles besser.
Sokrates.
[Gäste dürfen nur lesen]
| Beiträge: 1.477, Mitglied seit 16 Jahren |
Beitrag Nr. 13-351
16.03.2015 14:47
|
Hallo Eugen,
mfg okotombrok
P.S.: melde mich später noch zum Thema"Der Kopf ist rund, damit die Gedanken die Richtung wechseln können"
(Francis Picabia)
Bauhof schrieb in Beitrag Nr. 13-350:mit diesen Zahlen kann ich momentan nichts anfangen. Bitte teile mir die Zahlen deines Zwillingsexperiments in folgender Form mit:
1. Geschwindigkeit v des reisenden Zwillings aus der Sicht des ruhenden Zwillings.
2. Entfernung s des Umkehrpunktes aus der Sicht des ruhenden Zwillings.
Zitat von Claus:B fliege aus Sicht A mit v = 0,6c in 1,2 Lj Entfernung und kehre dort um.
mfg okotombrok
P.S.: melde mich später noch zum Thema
Signatur:
(Francis Picabia)
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 13-352
16.03.2015 17:41
|
Hallo Bauhof,
Wie Okotombrok bereits schrieb: zu 1.: v = 0,6c; zu 2.: s = 1,2 Lj
Es geht aber nicht darum den Altersunterschied zu bestimmen. Das habe ich in Beitrag Nr. 13-342 bereits getan.
Es geht darum zu erklären, warum Zwilling A (= der zu Hause Gebliebene) tatsächlich 4 Jahre älter wird, wenn doch B (der Reisende) wegen der bei A auftretenden Zeitdilatation berechnet, dass für A in den 3,2 Jahren seiner (also B´s) Reise nur t(A) = t(B) * 1/ γ = 3,2 Jahre * 0,8 = 2,56 Jahre vergehen.
Zum besseren Verständnis der Problematik folgende Zusatzaufgabe:
A trinke nach 2 Jahren seiner Zeit eine Tasse Kaffee. Wann erfolgt dieses Ereignis aus der Sicht von B?
Bauhof schrieb in Beitrag Nr. 13-350:Bitte teile mir die Zahlen deines Zwillingsexperiments in folgender Form mit:
1. Geschwindigkeit v des reisenden Zwillings aus der Sicht des ruhenden Zwillings.
2. Entfernung s des Umkehrpunktes aus der Sicht des ruhenden Zwillings.
Dann werde ich den Altersunterschied berechnen.
Wie Okotombrok bereits schrieb: zu 1.: v = 0,6c; zu 2.: s = 1,2 Lj
Es geht aber nicht darum den Altersunterschied zu bestimmen. Das habe ich in Beitrag Nr. 13-342 bereits getan.
Es geht darum zu erklären, warum Zwilling A (= der zu Hause Gebliebene) tatsächlich 4 Jahre älter wird, wenn doch B (der Reisende) wegen der bei A auftretenden Zeitdilatation berechnet, dass für A in den 3,2 Jahren seiner (also B´s) Reise nur t(A) = t(B) * 1/ γ = 3,2 Jahre * 0,8 = 2,56 Jahre vergehen.
Zum besseren Verständnis der Problematik folgende Zusatzaufgabe:
A trinke nach 2 Jahren seiner Zeit eine Tasse Kaffee. Wann erfolgt dieses Ereignis aus der Sicht von B?
[Gäste dürfen nur lesen]
| Beiträge: 936, Mitglied seit 13 Jahren |
Beitrag Nr. 13-353
16.03.2015 21:28
|
Claus
Wir sehen einen Körper in der Aufsicht als Quadrat. Denselben Körper sehen wir in der Frontansicht als Quadrat.
Wie schaut der Köper in der Seitenansicht aus? Wer in der Seitenansicht ebenfalls ein Quadrat erwartet und als
einzige Schlussfolgerung einen Würfel als Resultat aller Vorstellungen für möglich hält, könnte möglicherweise
enttäuscht werden.
Bei physikalischen Vorstellungen wird uns nur allzu oft ein Würfel als Maß aller Erkenntnisse aufgezwungen.
Edwin Hubble hat die Rotverschiebung der Galaxien entdeckt.
Edwin Hubble hat nicht die Ausdehnung des Universums entdeckt.
Daher - Einspruch gegen alle Urknaller.
Die Beobachtung, dass eine Uhr in einem bewegten System langsamer „tickt“ als in einem scheinbar ruhendem System
(falls es ein solches [ruhendes] den geben sollte)
zeigt nur das eine Uhr beeinflusst wird und erklärt weder Zeit noch ändert oder verbiegt sich die Gegenwart.
Daher – Einspruch gegen differierend alternde Zwillinge.
mfg Harald
Mein Einspruch gegen Urknaller und Uhrenableser ist nicht polemisch zu interpretieren,
sondern soll dem verständnisvollen Leser die Möglichkeit offen lassen - zeigen das Würfel
durchaus auch anders zu interpretieren sind und entsprechende Argumente den Würfel
bis zur Unkenntlichkeit, durch eigenes Denken, fallen lassen.
:ape: :coffee:
:coffee: Es gibt nur eine Zeit - die aktive und die passive Gegenwart - und Gravitation
Es gibt nur eine Zeit - die aktive und die passive Gegenwart - und Gravitation
ist die Antwort der Gegenwart auf die Einwirkung vergangener Wichtigkeiten.
Wir sehen einen Körper in der Aufsicht als Quadrat. Denselben Körper sehen wir in der Frontansicht als Quadrat.
Wie schaut der Köper in der Seitenansicht aus? Wer in der Seitenansicht ebenfalls ein Quadrat erwartet und als
einzige Schlussfolgerung einen Würfel als Resultat aller Vorstellungen für möglich hält, könnte möglicherweise
enttäuscht werden.
Bei physikalischen Vorstellungen wird uns nur allzu oft ein Würfel als Maß aller Erkenntnisse aufgezwungen.
Edwin Hubble hat die Rotverschiebung der Galaxien entdeckt.
Edwin Hubble hat nicht die Ausdehnung des Universums entdeckt.
Daher - Einspruch gegen alle Urknaller.
Die Beobachtung, dass eine Uhr in einem bewegten System langsamer „tickt“ als in einem scheinbar ruhendem System
(falls es ein solches [ruhendes] den geben sollte)
zeigt nur das eine Uhr beeinflusst wird und erklärt weder Zeit noch ändert oder verbiegt sich die Gegenwart.
Daher – Einspruch gegen differierend alternde Zwillinge.
mfg Harald
Mein Einspruch gegen Urknaller und Uhrenableser ist nicht polemisch zu interpretieren,
sondern soll dem verständnisvollen Leser die Möglichkeit offen lassen - zeigen das Würfel
durchaus auch anders zu interpretieren sind und entsprechende Argumente den Würfel
bis zur Unkenntlichkeit, durch eigenes Denken, fallen lassen.
:ape:
 :coffee:
:coffee:
Signatur:
ist die Antwort der Gegenwart auf die Einwirkung vergangener Wichtigkeiten.
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 13-354
17.03.2015 05:14
|
Harald Denifle schrieb in Beitrag Nr. 13-353:... den Würfel
bis zur Unkenntlichkeit, durch eigenes Denken, fallen lassen.
Harald
so ein ausgedachter Würfel hat ja unendlich viele Möglichkeiten, wie er wohl aussehen könnte.
Wenn man aber dem wahren Würfel auf den Fersen ist, sollte man - wenn's schwierig wird - sich nicht einem leichteren, dafür aber wieder nur ausgedachten Würfel zuwenden.
[Gäste dürfen nur lesen]
| Beiträge: 1.375, Mitglied seit 16 Jahren |
Beitrag Nr. 13-355
17.03.2015 12:42
|
Hallo Claus,Claus schrieb in Beitrag Nr. 13-352:Es geht darum zu erklären, warum Zwilling A (= der zu Hause Gebliebene) tatsächlich 4 Jahre älter wird, wenn doch B (der Reisende) wegen der bei A auftretenden Zeitdilatation berechnet, dass für A in den 3,2 Jahren seiner (also B´s) Reise nur t(A) = t(B) * 1/ γ = 3,2 Jahre * 0,8 = 2,56 Jahre vergehen.
bei diesem Problem kann ich deiner Argumentation leider nicht folgen, sondern ich folge der Argumentation von Franz Embacher. Er schreibt:
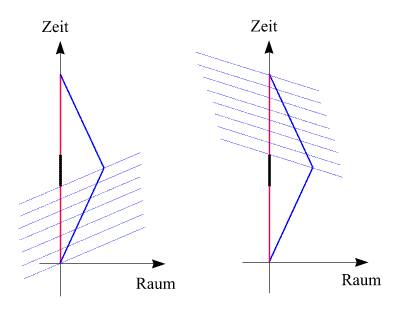
Zitat:Um das genauer zu analysieren, stellen wir uns vor, dass sich die Schwester ab und zu fragt, was denn der Bruder "jetzt gerade" macht. Wenn das "jetzt" die Gleichzeitigkeit ihrem eigenen Ruhsystem bedeutet, so hängt die Antwort auf ihre Frage davon ab, ob sie sich noch am Hinweg oder bereits am Rückweg befindet. Das wird in diesen beiden Raumzeit-Diagrammen deutlich:
Im linken Diagramm sind einige Linien eingezeichnet. Alle Ereignisse auf jeder dieser Linien finden für die Schwester gleichzeitig statt, wenn sie sich am Hinweg befindet. Im rechten Diagramm sind die entsprechenden Linien "konstanter Zeit" für den zweiten Teil der Reise eingezeichnet:
Alle Ereignisse auf jeder dieser Linien finden für die Schwester gleichzeitig statt, wenn sie sich am Rückweg befindet. Wir sehen, dass es einen Bereich von Ereignissen im Leben des Bruders gibt, die die Schwester in keinem ihrer beiden Inertialsysteme jemals als "jetzt" klassifizieren würde − er ist auf seiner Weltlinie in schwarz gekennzeichnet. Würden in der Formel (2) einfach T und T ' vertauscht, wäre sie falsch. Es gilt aber (aufgrund der Zeitdilatation, diesmal mit vertauschten Rollen von Schwester und Bruder)
T’ = T’’ / sqrt(1 – v²/c²)
wobei T'' jener Anteil der Eigenzeit des Bruders ist, von dem die Dauer des schwarzen Bereichs abgezogen wurde. Das Gegenargument ist damit zurechtgerückt: Es ist gewissermaßen die schwarze "Lücke", die es hinfällig macht.
Der schwarze Bereich in deinem Zwillingsexperiment beträgt 4 – 3,2 = 0,8 Jahre. Wenn man den schwarzen Bereich in deinem Zwillingsexperiment von der Zeit des ruhenden Zwillings abzieht, erhält man T’’ = 4 – 0,8 = 3,2 Jahre.
Somit ergibt sich aus der Sicht des reisenden Zwillings die Zeit T' des ruhenden Zwillings wie folgt:
T’ = T’’/sqrt(1 – v²/c²)
T’ = 3,2/0,8
T’ = 4 Jahre
Mir erscheint das plausibel, was Franz Embacher schreibt. Ich sehe nicht, dass man in die SRT auf die Lichtlaufzeiten zurückgreifen müsste, um das Problem zu lösen. Ich denke Franz Embacher hat das Problem gelöst, ohne die Lichtlaufzeiten einzubeziehen.
M.f.G. Eugen Bauhof
Signatur:
der Normale aus seinen Erfahrungen,
und der Dumme weiß alles besser.
Sokrates.
Beitrag zuletzt bearbeitet von Bauhof am 17.03.2015 um 15:38 Uhr.
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 13-356
18.03.2015 20:11
|
Hallo zusammen,
wie ich in Beitrag Nr. 13-344 gezeigt hatte, altert A während der 3,2-jährigen Hin- und Rückreise von B um 4 Jahre;
dabei „vergehen“ bei A aus der Sicht von B jedoch nur 2,56 Jahre.
Dies scheint auf den ersten Blick ein Widerspruch zu sein, bei genauerer Untersuchung ist dies jedoch nicht der Fall, denn:
Die scheinbare Diskrepanz erklärt sich dadurch, dass für B am Umkehrpunkt ein „Zeitsprung“ in A stattfindet, bei dem die Uhr von A instantan von 1,28 auf 2,72 Jahre vorrückt. Die beiden übrig gebliebenen Zeitintervalle a) [0 bis 1,28 Jahre] und b) [2,72 bis 4 Jahre] bilden zusammen genau die Zeitdauer, die sich während der 3,2-jährigen Reise von B in A bei Berücksichtigung der Zeitdilatation ereignet, nämlich 3,2 * 0,8 = 2,56 Jahre.
Gemäß SRT ist für das dazwischen liegende Zeitintervall von A [1,28 bis 2,72 Jahre] keine Gleichzeitigkeit in B definiert; d.h.: wenn A bspw. im Jahr 2 nach dem Start frühstückt, fände dieses Frühstück zu keinem Zeitpunkt während der Reise von B statt.
Nun kann B aber während der Reise zweifelsfrei feststellen, dass das Frühstück in A stattfindet - denn er kann es einfach mit dem Teleskop beobachten. Das Frühstück ist somit eine während der Reise durch Experiment feststellbare Tatsache - so, wie auch jeder andere Zeitpunkt der 4-jährigen Geschichte von A in lückenloser kausaler Folge eine experimentelle Tatsache ist.
Aus diesem Grunde muss B nach meiner Auffassung zur Erklärung der vollständigen Geschichte von A die Lichtlaufzeit einbeziehen. Nur dann ist nämlich jedem Zeitpunkt der sichtbaren Geschichte von A (in der u.a. Formel mit tAvis bezeichnet) ein eindeutiger Zeitpunkt in B wie folgt zugeordnet:
für 0 <= tB <= 1,6 gilt: tAvis = tB * 0,5
für 1,6 <= tB <= 3,2 gilt: tAvis = 2*tB - 2,4
wie ich in Beitrag Nr. 13-344 gezeigt hatte, altert A während der 3,2-jährigen Hin- und Rückreise von B um 4 Jahre;
dabei „vergehen“ bei A aus der Sicht von B jedoch nur 2,56 Jahre.
Dies scheint auf den ersten Blick ein Widerspruch zu sein, bei genauerer Untersuchung ist dies jedoch nicht der Fall, denn:
Die scheinbare Diskrepanz erklärt sich dadurch, dass für B am Umkehrpunkt ein „Zeitsprung“ in A stattfindet, bei dem die Uhr von A instantan von 1,28 auf 2,72 Jahre vorrückt. Die beiden übrig gebliebenen Zeitintervalle a) [0 bis 1,28 Jahre] und b) [2,72 bis 4 Jahre] bilden zusammen genau die Zeitdauer, die sich während der 3,2-jährigen Reise von B in A bei Berücksichtigung der Zeitdilatation ereignet, nämlich 3,2 * 0,8 = 2,56 Jahre.
Gemäß SRT ist für das dazwischen liegende Zeitintervall von A [1,28 bis 2,72 Jahre] keine Gleichzeitigkeit in B definiert; d.h.: wenn A bspw. im Jahr 2 nach dem Start frühstückt, fände dieses Frühstück zu keinem Zeitpunkt während der Reise von B statt.
Nun kann B aber während der Reise zweifelsfrei feststellen, dass das Frühstück in A stattfindet - denn er kann es einfach mit dem Teleskop beobachten. Das Frühstück ist somit eine während der Reise durch Experiment feststellbare Tatsache - so, wie auch jeder andere Zeitpunkt der 4-jährigen Geschichte von A in lückenloser kausaler Folge eine experimentelle Tatsache ist.
Aus diesem Grunde muss B nach meiner Auffassung zur Erklärung der vollständigen Geschichte von A die Lichtlaufzeit einbeziehen. Nur dann ist nämlich jedem Zeitpunkt der sichtbaren Geschichte von A (in der u.a. Formel mit tAvis bezeichnet) ein eindeutiger Zeitpunkt in B wie folgt zugeordnet:
für 0 <= tB <= 1,6 gilt: tAvis = tB * 0,5
für 1,6 <= tB <= 3,2 gilt: tAvis = 2*tB - 2,4
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 13-357
18.03.2015 20:14
|
Hallo Bauhof,
m.E. beträgt die schwarze Lücke nicht 4 - 3,2 = 0,8 Jahre sondern 4 - (3,2 * 0,8) = 1,44 Jahre (aber das ist nicht wesentlich für die prinzipiellen Überlegungen).
Wenn Franz Embacher schreibt:
so stimme ich ihm bis auf das Wort "würde" zu. Ohne Lichtlaufzeiten ist diese Lücke gleichzeitiger Ereignisse immer vorhanden. Nur unter Einbezug der Lichtlaufzeiten entfällt eine solche Lücke.
m.E. beträgt die schwarze Lücke nicht 4 - 3,2 = 0,8 Jahre sondern 4 - (3,2 * 0,8) = 1,44 Jahre (aber das ist nicht wesentlich für die prinzipiellen Überlegungen).
Wenn Franz Embacher schreibt:
Zitat:Wir sehen, dass es einen Bereich von Ereignissen im Leben des Bruders gibt, die die Schwester in keinem ihrer beiden Inertialsysteme jemals als "jetzt" klassifizieren würde
so stimme ich ihm bis auf das Wort "würde" zu. Ohne Lichtlaufzeiten ist diese Lücke gleichzeitiger Ereignisse immer vorhanden. Nur unter Einbezug der Lichtlaufzeiten entfällt eine solche Lücke.
[Gäste dürfen nur lesen]
| Beiträge: 1.375, Mitglied seit 16 Jahren |
Beitrag Nr. 13-358
19.03.2015 11:46
|
Claus schrieb in Beitrag Nr. 13-352:Es geht darum zu erklären, warum Zwilling A (= der zu Hause Gebliebene) tatsächlich 4 Jahre älter wird, wenn doch B (der Reisende) wegen der bei A auftretenden Zeitdilatation berechnet, dass für A in den 3,2 Jahren seiner (also B´s) Reise nur t(A) = t(B) * 1/ γ = 3,2 Jahre * 0,8 = 2,56 Jahre vergehen.
Hallo Claus,
jetzt erst bemerke ich, dass dir ein Rechenfehler unterlaufen ist. Du schreibst:
tA) = t(B) * 1/ γ = 3,2 Jahre * 0,8 = 2,56 Jahre. Zuerst dividierst du durch γ und beim Zahleneinsetzen multiplizierst du mit γ?
Wenn tA) = t(B) * 1/ γ und γ = 0,8 ist, dann kommt:
tA) = t(B) * 1/ γ = 3,2 Jahre / 0,8 = 4 Jahre. Richtig?
Das ist das gleiche Ergebnis, zu dem ich mit Hilfe der Überlegungen von Franz Embacher auch gekommen bin.
Claus schrieb in Beitrag Nr. 13-357:m.E. beträgt die schwarze Lücke nicht 4 - 3,2 = 0,8 Jahre sondern 4 - (3,2 * 0,8) = 1,44 Jahre (aber das ist nicht wesentlich für die prinzipiellen Überlegungen).
Die Lücke, ob man sie nun schwarz nennt oder nicht, ergibt sich m.E. wie folgt: Die Eigenzeit von A beträgt 4 Jahre. Die Eigenzeit von B beträgt 3,2 Jahre. Was man überhaupt als Lücke bezeichnen kann, kann doch nur die Differenz von beiden Eigenzeiten sein, nämlich 4 – 3,2 = 0,8 Jahre. Wie würdest du es begründen?
Claus schrieb in Beitrag Nr. 13-357:Wenn Franz Embacher schreibt:
Zitat:Wir sehen, dass es einen Bereich von Ereignissen im Leben des Bruders gibt, die die Schwester in keinem ihrer beiden Inertialsysteme jemals als "jetzt" klassifizieren würde
so stimme ich ihm bis auf das Wort "würde" zu. Ohne Lichtlaufzeiten ist diese Lücke gleichzeitiger Ereignisse immer vorhanden. Nur unter Einbezug der Lichtlaufzeiten entfällt eine solche Lücke.
Diese Lücke im “Jetzt“ von A und B ist m.E. etwas grundsätzliches, das durch die Physik der relativistischen Raumzeit gegeben ist. Ich sehe nicht, wie man diese Lücke durch Einbezug von Lichtlaufzeiten zum Verschwinden bringen könnte.
Aber ich kann natürlich etwas übersehen. Vielleicht stellst du mir deine Herleitung in übersichtlicher Weise als PFD zur Verfügung. Dann würde ich es mit deiner Erlaubnis bei quanten.de veröffentlichen und zur Diskussion stellen. Denn dort gibt es mehrere Physik-Profis, die das bestimmt abschließend beurteilen können. Du kannst deine Herleitung natürlich auch selbst dort als Betrag einbringen.
M.f.G. Eugen Bauhof
Signatur:
der Normale aus seinen Erfahrungen,
und der Dumme weiß alles besser.
Sokrates.
[Gäste dürfen nur lesen]
| Beiträge: 1.477, Mitglied seit 16 Jahren |
Beitrag Nr. 13-359
19.03.2015 14:54
|
Hallo Claus,
ja, jetzt hab ich's gefressen!
Da ist ein Widerspruch der nicht einfach unter den Tisch gekehrt werden kann, auch wenn er sich rechnerisch umgehen lässt.
Ich habe dazu meine Fachliteratur bemüht (keine populärwissenschaftliche, da wird es oft ignoiiert) und dort wird auf den Widerspruch hingewiesen und eingegangen.
Ich werde mich später dazu äußern, bin gerade an der Arbeit.
mfg okotombrok"Der Kopf ist rund, damit die Gedanken die Richtung wechseln können"
(Francis Picabia)
Claus schrieb in Beitrag Nr. 13-349:Die Zeitdilatation, die B bei A berechnet, führt jedoch ungeachtet der aus Sicht B geringeren Distanz dazu, dass bei A während der 3,2jährigen Reise nur 2,56 Jahre vergehen. Daher müsste A doch während der Dauer des Hin- und Rückflugs auch nur diese 2,56 Jahre gealtert sein. Tatsächlich ist er aber um 4 Jahre gealtert. Daher die an Bauhof gerichtete Frage auch an dich, der du dich einmal in die Lage von B versetzen mögest: Wie erklärst du das?
ja, jetzt hab ich's gefressen!
Da ist ein Widerspruch der nicht einfach unter den Tisch gekehrt werden kann, auch wenn er sich rechnerisch umgehen lässt.
Ich habe dazu meine Fachliteratur bemüht (keine populärwissenschaftliche, da wird es oft ignoiiert) und dort wird auf den Widerspruch hingewiesen und eingegangen.
Ich werde mich später dazu äußern, bin gerade an der Arbeit.
mfg okotombrok
Signatur:
(Francis Picabia)
[Gäste dürfen nur lesen]
| Beiträge: 1.375, Mitglied seit 16 Jahren |
Beitrag Nr. 13-360
19.03.2015 15:31
|
Okotombrok schrieb in Beitrag Nr. 13-359:Hallo Claus,
ja, jetzt hab ich's gefressen!Claus schrieb in Beitrag Nr. 13-349:Die Zeitdilatation, die B bei A berechnet, führt jedoch ungeachtet der aus Sicht B geringeren Distanz dazu, dass bei A während der 3,2jährigen Reise nur 2,56 Jahre vergehen. Daher müsste A doch während der Dauer des Hin- und Rückflugs auch nur diese 2,56 Jahre gealtert sein. Tatsächlich ist er aber um 4 Jahre gealtert. Daher die an Bauhof gerichtete Frage auch an dich, der du dich einmal in die Lage von B versetzen mögest: Wie erklärst du das?
Da ist ein Widerspruch der nicht einfach unter den Tisch gekehrt werden kann, auch wenn er sich rechnerisch umgehen lässt.
Hallo Okotombrok,
nein, ich habe es noch nicht gefressen! Ich bezweifle, dass es da überhaupt etwas zu “fressen“ gibt.
Okotombrok schrieb in Beitrag Nr. 13-359:Ich habe dazu meine Fachliteratur bemüht (keine populärwissenschaftliche, da wird es oft ignoiiert) und dort wird auf den Widerspruch hingewiesen und eingegangen. Ich werde mich später dazu äußern, bin gerade an der Arbeit.
Da bin ich sehr gespannt, wie sich die Fachliteratur zu dem scheinbaren Widerspruch äußert.
M.f.G. Eugen Bauhof
Signatur:
der Normale aus seinen Erfahrungen,
und der Dumme weiß alles besser.
Sokrates.
Beitrag zuletzt bearbeitet von Bauhof am 19.03.2015 um 15:32 Uhr.
[Gäste dürfen nur lesen]
|
Claus (Moderator)
Beiträge: 2.425, Mitglied seit 17 Jahren
|
Beitrag Nr. 13-361
19.03.2015 16:48
|
Bauhof schrieb in Beitrag Nr. 13-358:jetzt erst bemerke ich, dass dir ein Rechenfehler unterlaufen ist.
Noch sehe ich keinen Fehler.
Es wird 2x mit 0,8 multipliziert! Aus Sicht A dautert die Reise von B: 4*0,8 =3,2 Jahre.
Aus Sicht B vergehen bei A: 3,2*0,8=2,56 Jahre. Oder seh' ich da was falsch?
Zitat von Bauhof:Die Lücke, ob man sie nun schwarz nennt oder nicht, ergibt sich m.E. wie folgt: Die Eigenzeit von A beträgt 4 Jahre. Die Eigenzeit von B beträgt 3,2 Jahre. Was man überhaupt als Lücke bezeichnen kann, kann doch nur die Differenz von beiden Eigenzeiten sein, nämlich 4 – 3,2 = 0,8 Jahre. Wie würdest du es begründen?
Nein. Die Lücke ergibt sich aus den 4 tatsächlichen Jahren minus den 2,56 von B berechneten Jahren.
Bin jetzt unterwegs. Melde mich ggf. morgen abend.
[Gäste dürfen nur lesen]
In diesem Forum dürfen nur Mitglieder schreiben. Hier kannst du dich anmelden






 Nach oben
Nach oben